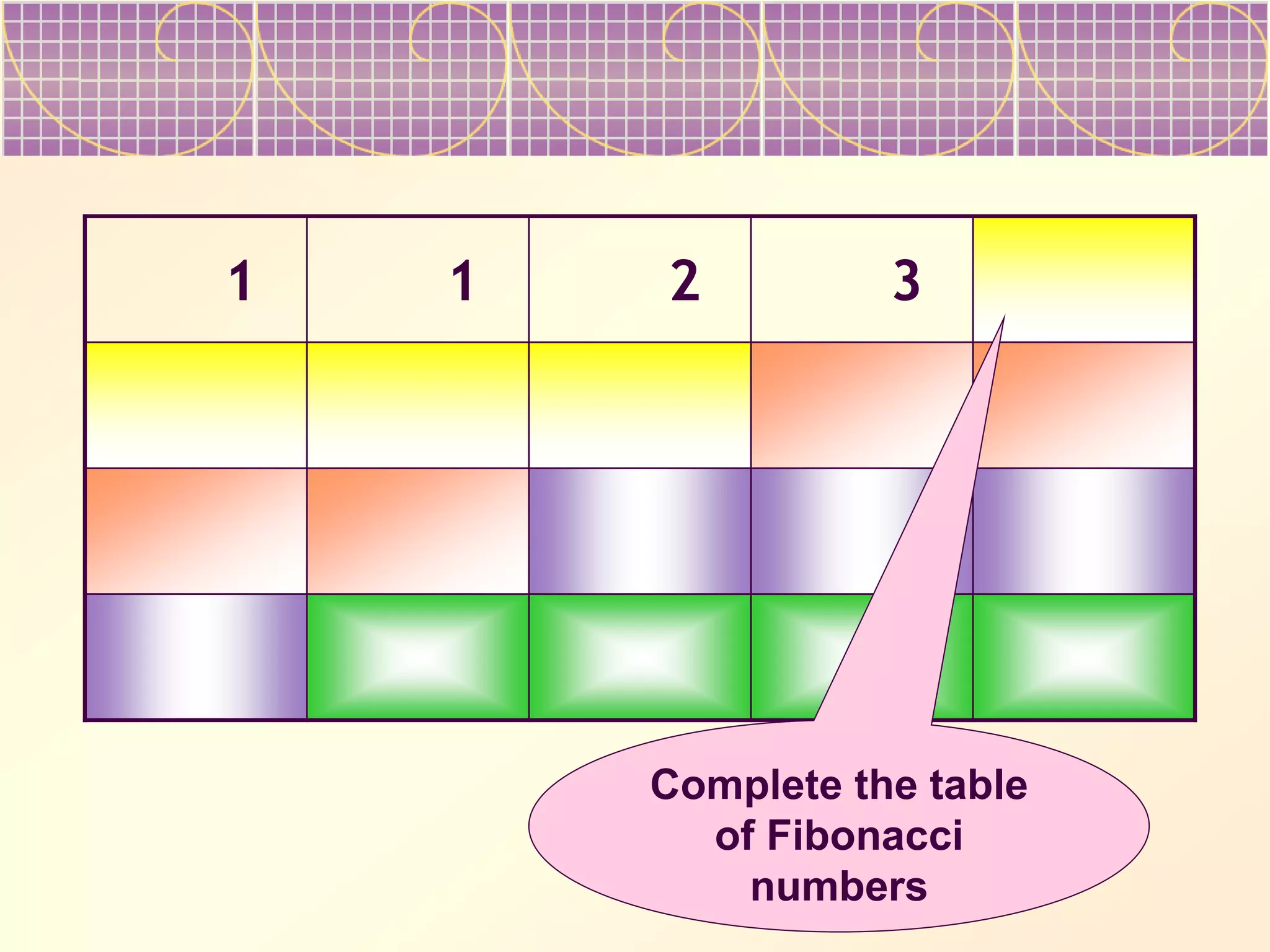
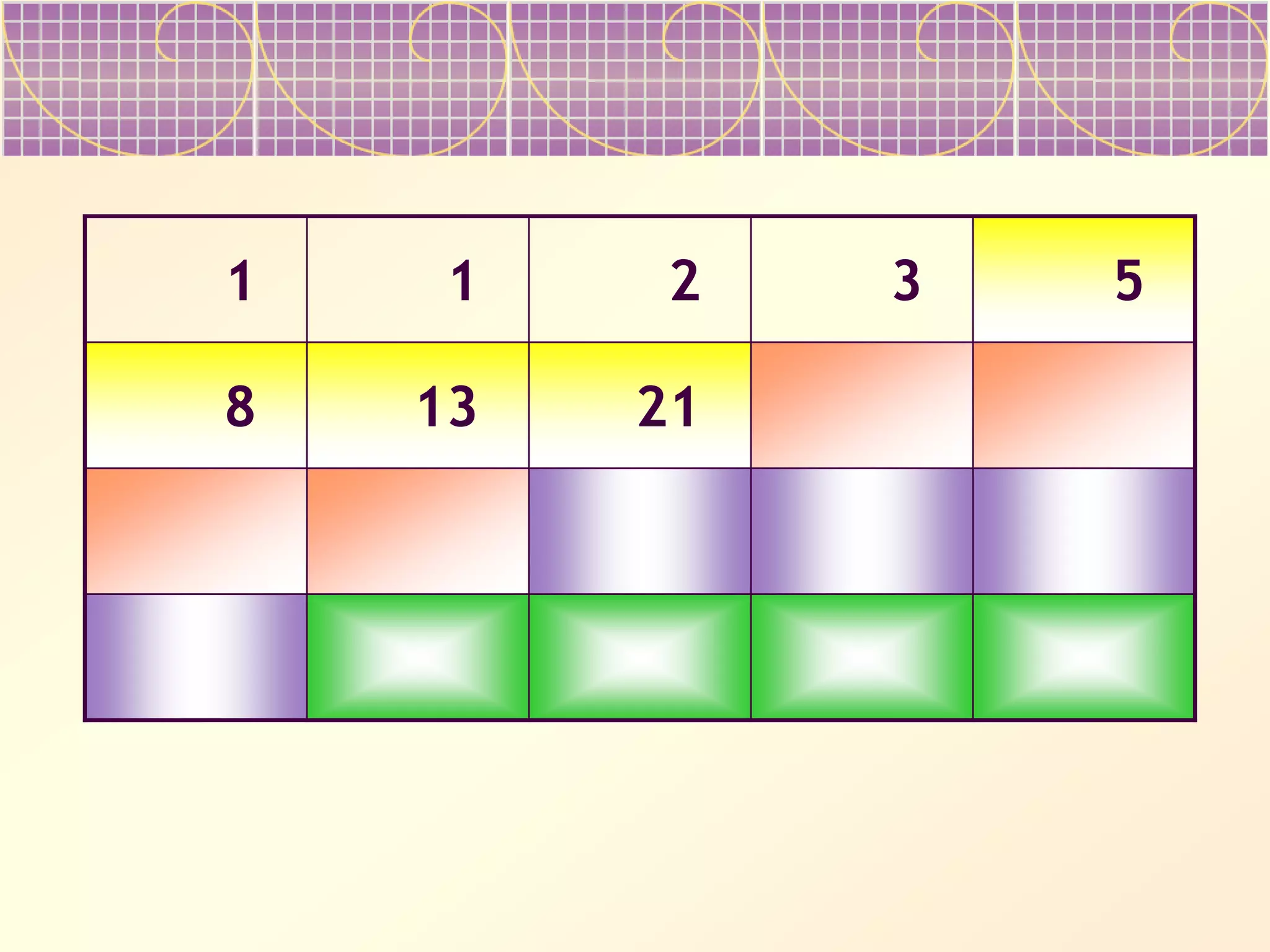
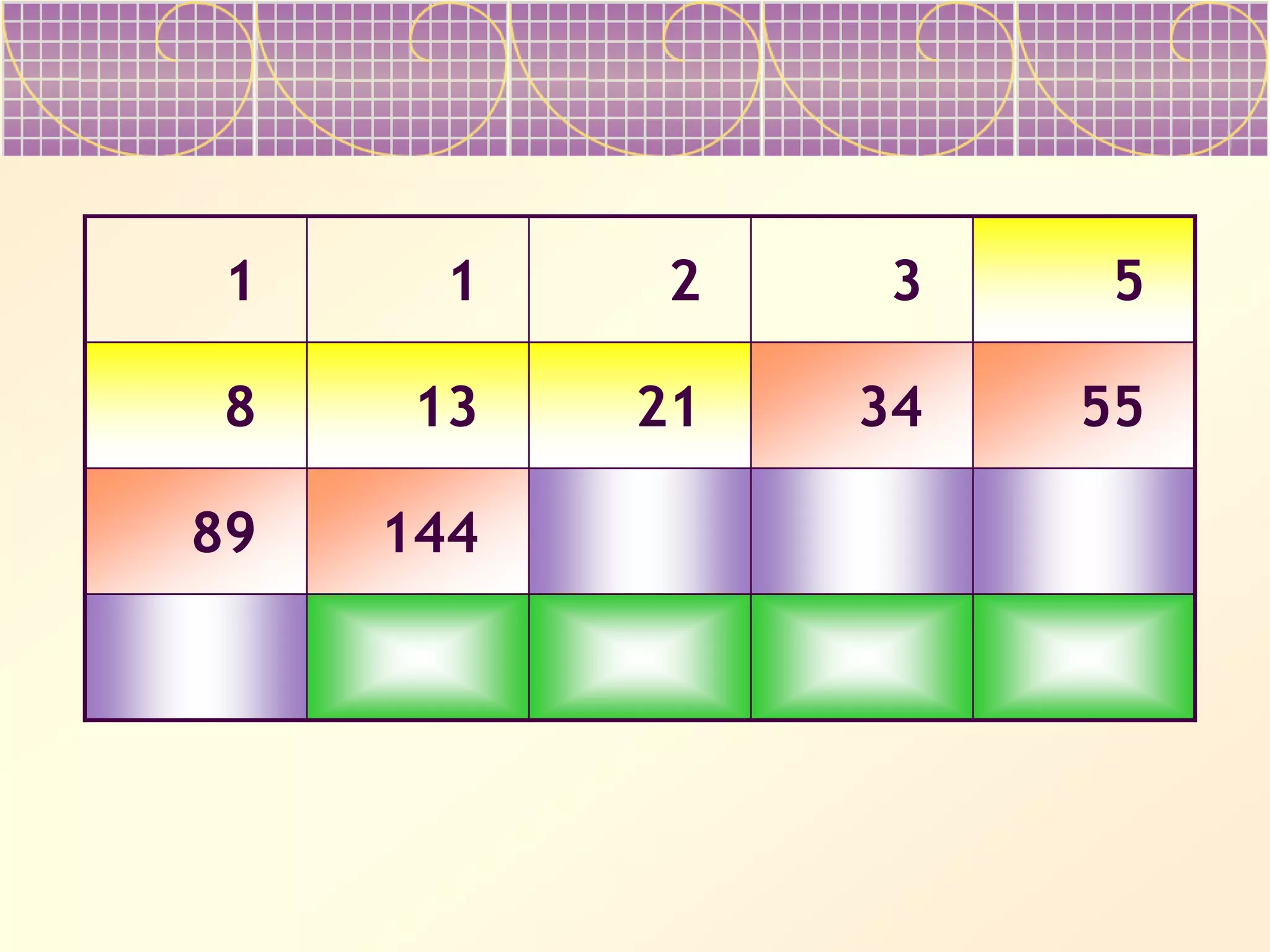
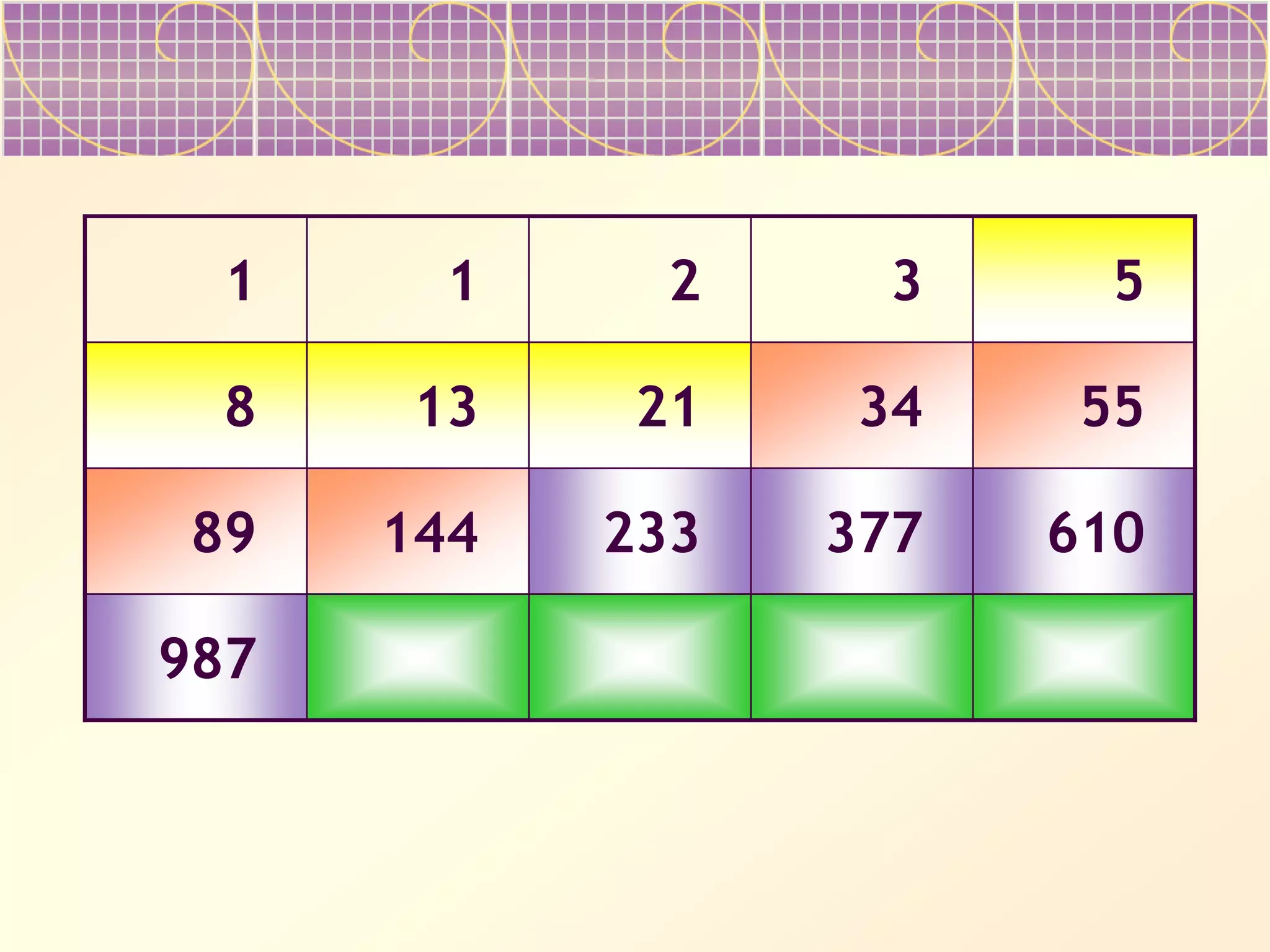
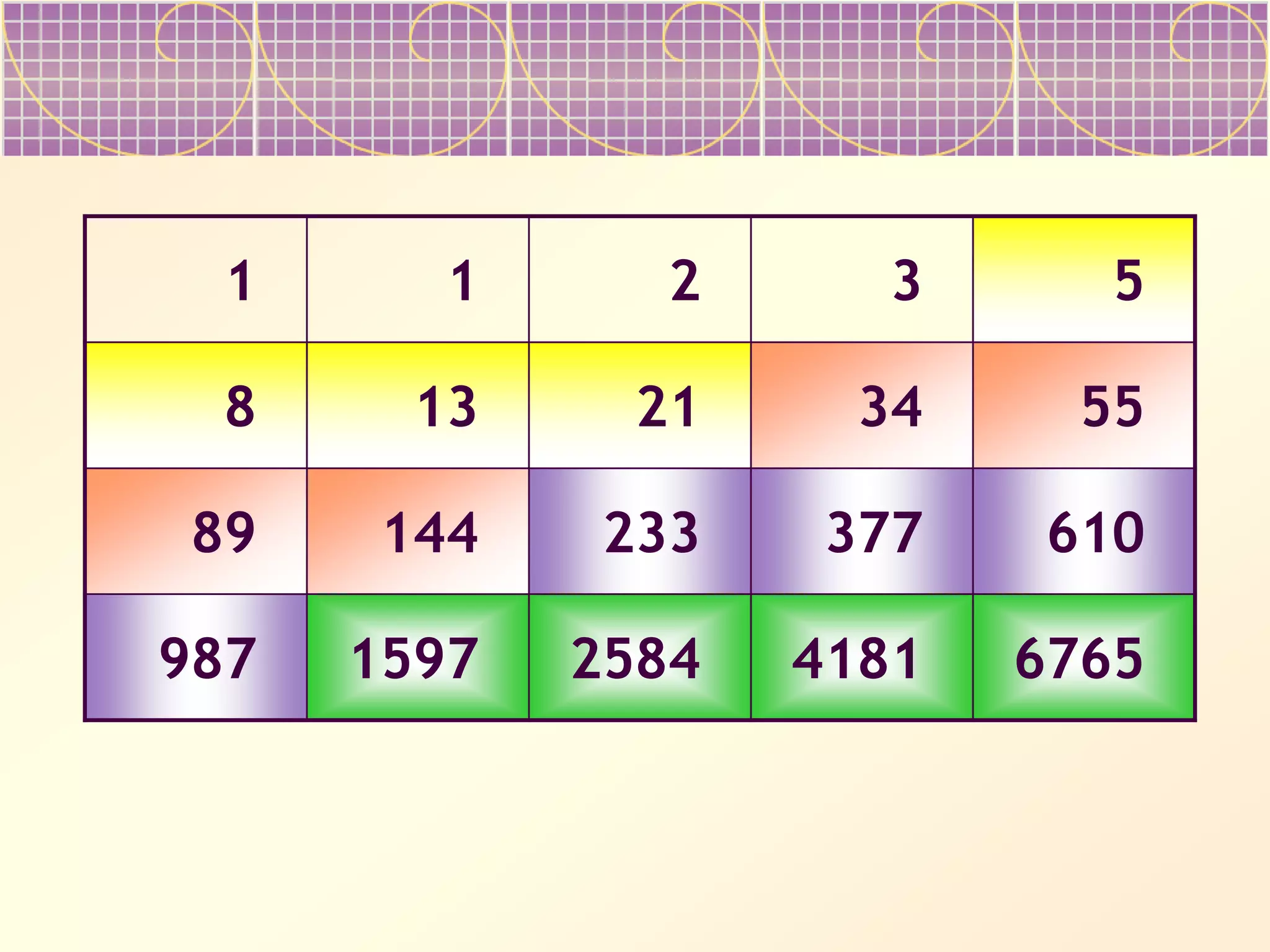
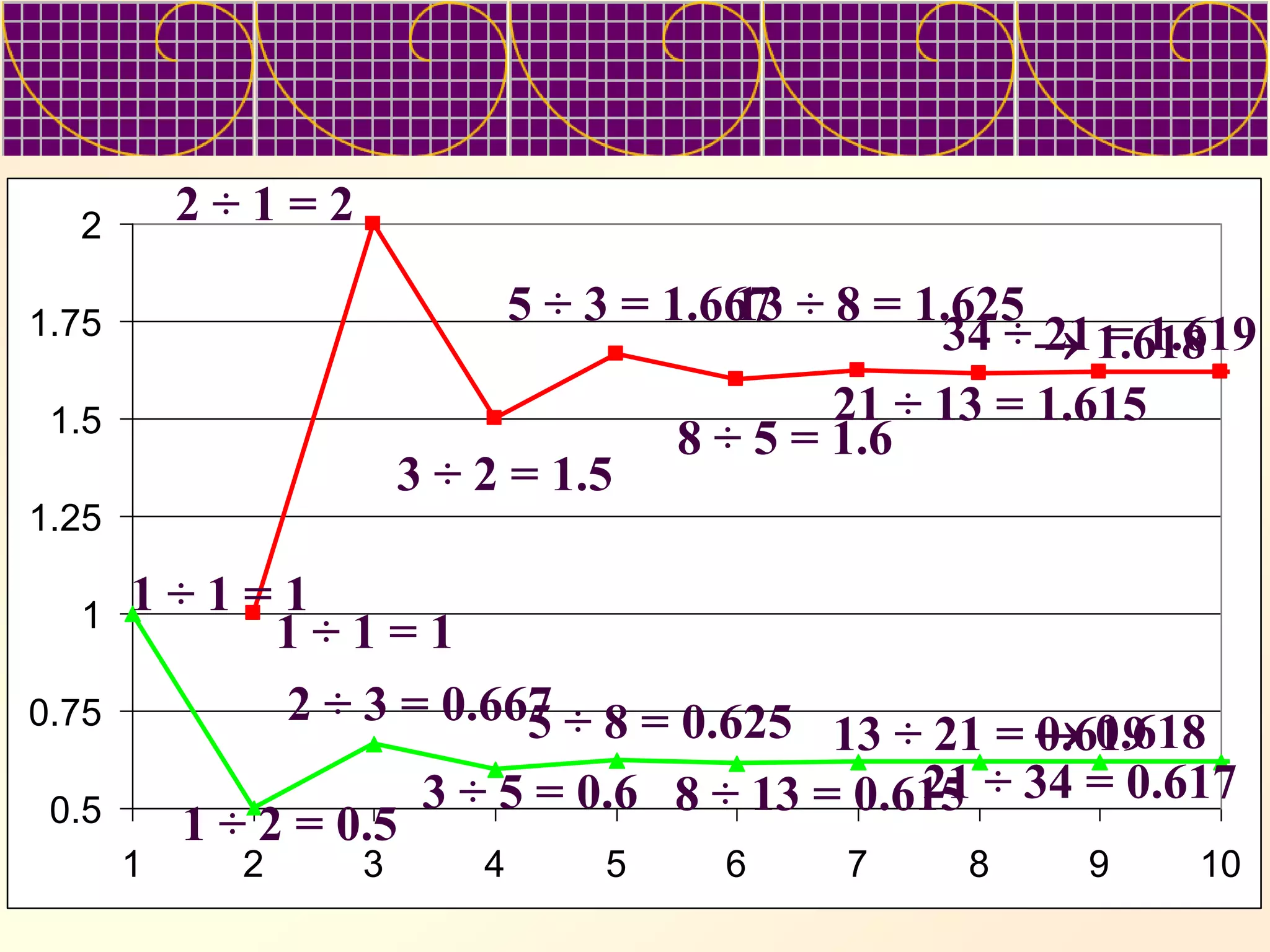
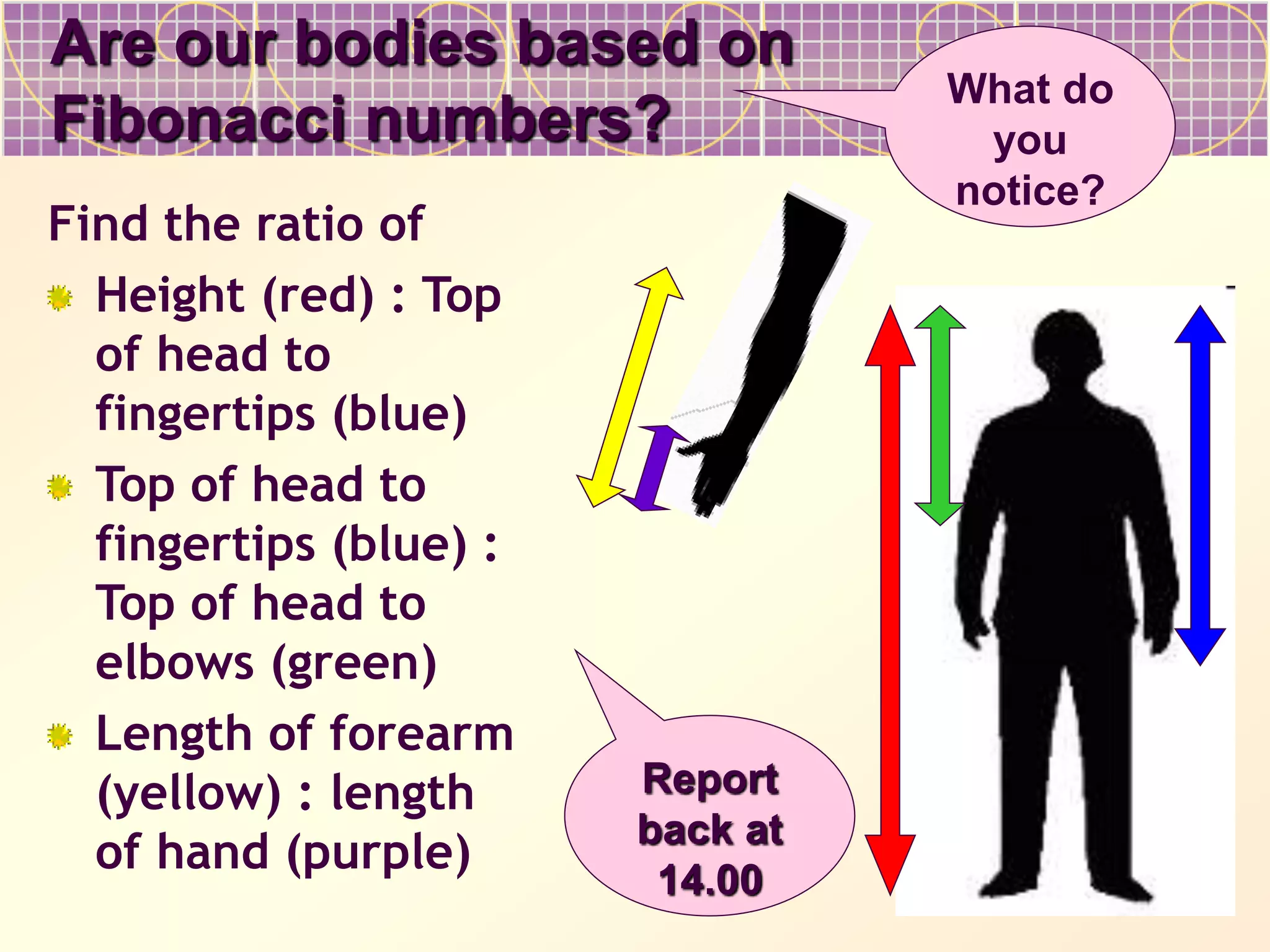
The document discusses Fibonacci numbers and their appearance in nature. It begins with an example of how Fibonacci numbers describe the efficient packing of seeds in sunflower heads and pine cones. It then provides background on Leonardo Fibonacci, who first introduced the sequence, and asks the reader to complete tables of the Fibonacci numbers. The document suggests Fibonacci numbers maximize efficiency in nature and describes properties like the ratios between successive terms approaching the golden ratio. It prompts the reader to consider ways Fibonacci numbers appear in art, architecture, biology and more.

1. Fibonacci
numbers
Month 0
1 pair
Month 1
1 pair
Month 2
2 pairs
Month 3
3 pairs
18 April, 2023
Jenny Gage
University of Cambridge

2. Introductions and preliminary task
Humphrey Davy – flowers
Seven Kings – flowers
John of Gaunt – pine cones or
pineapples
Ellen Wilkinson – pine cones or
pineapples

3. Fibonacci numbers in art and nature

4. Fibonacci numbers in nature
An example of efficiency in nature.
As each row of seeds in a sunflower or
pine cone, or petals on a flower grows,
it tries to put the maximum number in
the smallest space.
Fibonacci numbers are the whole
numbers which express the golden
ratio, which corresponds to the angle
which maximises number of items in
the smallest space.

5. Why are they called Fibonnaci numbers?
Leonardo of Pisa, c1175 – c1250
Liber Abaci, 1202, one of the first books to be
published by a European
One of the first people to introduce the decimal
number system into Europe
On his travels saw the advantage of the Hindu-
Arabic numbers compared to Roman numerals
Rabbit problem – in the follow-up work
About how maths is related to all kinds of things
you’d never have thought of

6. 1 1 2 3
Complete the table
of Fibonacci
numbers

7. 1 1 2 3 5
8 13 21

8. 1 1 2 3 5
8 13 21 34 55
89 144

9. 1 1 2 3 5
8 13 21 34 55
89 144 233 377 610
987

10. 1 1 2 3 5
8 13 21 34 55
89 144 233 377 610
987 1597 2584 4181 6765

11. Find the ratio of successive
Fibonacci numbers:
1 : 1, 2 : 1, 3 : 2, 5 : 3, 8 : 5, …
1 : 1, 1 : 2, 2 : 3, 3 : 5, 5 : 8, …
What do you notice?

12. 0.5
0.75
1
1.25
1.5
1.75
2
1 2 3 4 5 6 7 8 9 10
1 ÷ 1 = 1
2 ÷ 1 = 2
3 ÷ 2 = 1.5
5 ÷ 3 = 1.667
8 ÷ 5 = 1.6
13 ÷ 8 = 1.625
21 ÷ 13 = 1.615
34 ÷ 21 = 1.619
1 ÷ 1 = 1
1 ÷ 2 = 0.5
2 ÷ 3 = 0.667
3 ÷ 5 = 0.6
5 ÷ 8 = 0.625
8 ÷ 13 = 0.615
13 ÷ 21 = 0.619
21 ÷ 34 = 0.617
 1.618
 0.618

13. Some mathematical properties
of Fibonacci numbers
Try one or more of
these.
Try to find some
general rule or
pattern.
Go high enough to
see if your rules or
patterns break down
after a bit!
Justify your answers
if possible.
1. Find the sum of
the first 1, 2, 3, 4,
… Fibonacci
numbers
2. Add up F1, F1 + F3,
F1 + F3 + F5, …
3. Add up F2, F2 + F4,
F2 + F4 + F6, …
4. Divide each
Fibonacci number
by 11, ignoring any
remainders.
Report
back at
13.45 E W
J G
S K
H D

14. Are our bodies based on
Fibonacci numbers?
Find the ratio of
Height (red) : Top
of head to
fingertips (blue)
Top of head to
fingertips (blue) :
Top of head to
elbows (green)
Length of forearm
(yellow) : length
of hand (purple)
What do
you
notice?
Report
back at
14.00

15. Spirals
Use the worksheet,
and pencils,
compasses and rulers,
to create spirals based
on Fibonacci numbers
Compare your spirals
with this nautilus shell
Display of
spirals at 14.25

16. What have Fibonacci numbers got
to do with:
Pascal’s triangle
Coin combinations
Brick walls
Rabbits eating lettuces
Combine all that you want to say
into one report
Report
back at
14.53