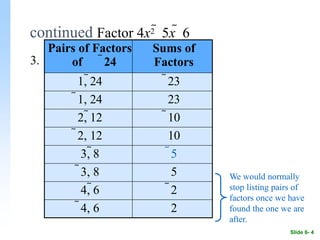
The document explains how to factor trinomials of the form ax² + bx + c using a step-by-step ac method, which includes factoring out the greatest common factor, finding pairs of factors, rewriting the middle term, and factoring by grouping. It provides specific examples such as factoring 4x² - 5x - 6 and 8x³ + 10x² - 12x, detailing each step of the process and verifying the solutions through multiplication. Additionally, it briefly discusses solving polynomial equations using factoring and determining the domain of a function.

1. Copyright © 2012 Pearson Education,
Inc.
Trinomials of
the
Type
ax2 + bx + c
■ Factoring Trinomials of the Type
ax2 + bx + c
■ Equations and Functions

2. To Factor ax2 + bx + c, Using the
ac- Method
1.Factor out the largest common factor, if
one exists.
2.Multiply the leading coefficient
a and the constant c.
3. Find a pair of factors ac whose sum is b.
4.Rewrite the middle term as
a sum or a difference using the factors
found in step (3).
5. Factor by grouping.
6.Include any common factor
from step (1) and check by multiplying.
Slide 6- 2

3. Example Factor 4x2  5x  6
Solution
1. First, we note that there is no common factor (other
than 1 or 1).
2. Multiply the leading coefficient, 4 and the
constant, 6:
(4)(6) = 24.
3. Try to factor 24 so that the sum of the
factors is 5:
Slide 6- 3

4. Pairs of Factors
of 24
Sums of
Factors
1, 24 23
1, 24 23
2, 12 10
2, 12 10
3, 8 5
3, 8 5
4, 6 2
4, 6 2
continued Factor 4x2  5x  6
3.
We would normally
stop listing pairs of
factors once we have
found the one we are
after.
Slide 6- 4

5. •4. Split 5x using the results of step (3):
• 5x = 8x + 3x.
•5. Factor by grouping:
Slide 6- 5
•
•
•
4x2  5x  6 = 4x2  8x + 3x  6
= 4x(x  2) + 3(x  2)
= (x  2)(4x + 3)
•We check the solution by multiplying or using a table. Check: (x  2)(4x
+ 3) = 4x2 + 3x  8x  6
• = 4x2  5x  6
•The factorization of 4x2  5x  6 is (x  2)(4x + 3).
continued Factor 4x2  5x  6

6. Example Factor 8x3 + 10x2  12x
Solution
1. We factor out the greatest common factor, 2x:
8x3 + 10x2  12x = 2x(4x2 + 5x  6)
2. To factor 4x2 + 5x  6 by grouping, we multiply
the leading coefficient, 4 and the constant
term (6): 4(6) = 24.
3. We next look for pairs of
factors of 24 whose
sum is 5.
Pairs of
Factors of
24
Sums of
Factors
3, 8 5
3, 8 5
Slide 6- 6

7. 4. We then rewrite the middle term: 4x2 + 5x  6 using
5x = 3x + 8x
5. Factor by grouping:
4x2 + 5x  6 = 4x2  3x + 8x  6
= x(4x  3) + 2(4x  3)
= (x + 2)(4x  3)
6. The factorization of the original trinomial
8x3 + 10x2  12x = 2x(x + 2)(4x  3).
Slide 6- 7
continued Factor 8x3 + 10x2  12x

8. Equations and
Functions
Slide 6- 8
•We now use our new factoring skills to solve a polynomial equation.
We factor a polynomial expression and use the principle of zero
products to solve the equation.

9. Example
Slide 6- 9
•Solve: 2x5 – 7x4 + 3x3 = 0.
•Solution--Algebraic
•We note that the polynomial has degree 5, so there will be at most 5
solutions of the equation.
• 2x5 – 7x4 + 3x3 = 0
• x3(2x – 1)(x – 3) = 0 Factoring
•x3 = 0
• x = 0
or 2x – 1 =
0
or x =
½
or x – 3 =
0
or x = 3
•The solutions are 0, ½ and 3.

10. Example
•Find the domain of F if F(x) =
•Solution
•The domain of F is the set of all values for which the function is a real
number. Since division by 0 is undefined, we exclude any x-value for which
the denominator is 0.
• x2 + 2x – 8 = 0
• (x – 2)(x + 4) = 0
•
•
x – 2 = 0
x = 2
or x + 4 = 0
or x = –4 These are the values to exclude.
•The domain of F is {x|x is a real number and x 2
•and x  4}.
x2
Slide 6- 10
x 1
 2x  8