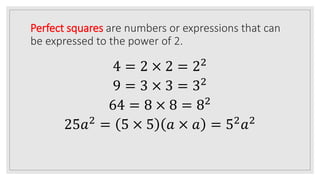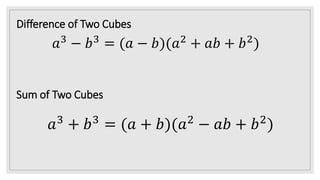Perfect squares and cubes are numbers that can be expressed as powers of 2 and 3 respectively. Examples are provided of numbers expressed as perfect squares and cubes. The power rule for exponents is reviewed. Students are asked to express given numbers and expressions in exponential form with powers of 3. Factorization identities are provided for the difference and sum of two cubes, and examples are worked through of factoring expressions involving the difference and sum of cubes.

1. REVIEW
PERFECT SQUARES

2. Perfect squares are numbers or expressions that can
be expressed to the power of 2.
4 = 2 × 2 = 22
9 = 3 × 3 = 32
64 = 8 × 8 = 82
25𝑎2 = 5 × 5 𝑎 × 𝑎 = 52𝑎2

3. Lesson 3

4. Perfect Cubes – numbers that can be expressed
to the power of 3.
8 = 2 × 2 × 2 = 23
27 = 3 × 3 × 3 = 33
64 = 4 × 4 × 4 = 43
8𝑥3
= 2 × 2 × 2 𝑥 × 𝑥 × 𝑥 = 23
𝑥3
8𝑦6
= 23
𝑦2 3
= 2𝑦2 3
Power Rule: 𝑎𝑚 𝑛
= 𝑎𝑚𝑛

5. Activity: Power of 3
Express the following in exponential form with a power of 3. Write your answers on you answer sheet.
1) 27
2)
1
8
3) 64𝑦3
4) 125𝑥3
5) 27𝑥6
𝑦12
= 3 × 3 × 3= 𝟑𝟑
=
1
2
×
1
2
×
1
2
=
= 43
𝑦3
=
= 53
𝑥3
=
= 33
𝑥2 3
𝑦4 3
=
𝟏
𝟐
𝟑
(𝟒𝒚)𝟑
(𝟓𝒙)𝟑
𝟑𝒙𝟐𝒚𝟒 𝟑

6. Difference of Two Cubes
𝑎3
− 𝑏3
= (𝑎 − 𝑏)(𝑎2
+ 𝑎𝑏 + 𝑏2
)
Sum of Two Cubes
𝑎3
+ 𝑏3
= (𝑎 + 𝑏)(𝑎2
− 𝑎𝑏 + 𝑏2
)

7. 1. Factor 𝑦3
− 27
(𝑦)3
−(33
)
𝑎 = 𝑦
𝑏 = 3
(𝑦)3
− 3 3
= 𝑦 − 3 𝑦2
+ 3𝑦 + 32
= 𝒚 − 𝟑 𝒚𝟐
+ 𝟑𝒚 + 𝟗
𝑎3
− 𝑏3
= (𝑎 − 𝑏)(𝑎2
+ 𝑎𝑏 + 𝑏2
)

8. 2. Factor 8𝑥3
− 64
*Note that 8𝑥3
− 64 has a GCMF which is 8 so rewrite the equation to
𝟖(𝒙𝟑
− 𝟖)
(𝑥)3
−(2)3
𝑎 = 𝑥
𝑏 = 2
8 𝑥 3
− 2 3
= 8 𝑥 − 2 𝑥2
+ 2𝑥 + 22
= 𝟖 𝒙 − 𝟐 𝒙𝟐
+ 𝟐𝒙 + 𝟒
𝑎3
− 𝑏3
= (𝑎 − 𝑏)(𝑎2
+ 𝑎𝑏 + 𝑏2
)

9. 3. Factor 27𝑚4
− 8𝑚𝑛6
*Note that it contains a GCMF which is 𝒎, so we are going to extract the GCMF
𝑚(27𝑚3
− 8𝑛6
)
(3𝑚)3
− 2𝑛2 3
𝑎 = 3𝑚
𝑏 = 2𝑛2
𝑎3
− 𝑏3
= (𝑎 − 𝑏)(𝑎2
+ 𝑎𝑏 + 𝑏2
)
m 3𝑚 3 − 2𝑛2 3
= 𝑚 3𝑚 − 2𝑛2
(3𝑚)2
+(3𝑚)(2𝑛2
) + 2𝑛2 2
= 𝒎 𝟑𝒎 − 𝟐𝒏𝟐 𝟗𝒎𝟐 + 𝟔𝒎𝒏𝟐 + 𝟒𝒏𝟒

10. 4. Factor 1 + 8𝑘3
(1)3− 2𝑘 2
𝑎 = 1
𝑏 = 2𝑘
(1)3
+ 2𝑘 3
= 1 + 2𝑘 12
− 1(2𝑘) + 2𝑘 2
= 𝟏 + 𝟐𝒌 𝟏 − 𝟐𝒌 + 𝟒𝒌𝟐
𝑎3
+ 𝑏3
= (𝑎 + 𝑏)(𝑎2
− 𝑎𝑏 + 𝑏2
)

11. 5. Factor 5ℎ + 40ℎ𝑘3
*Note that it contains a GCMF which is 𝟓𝒉, so we are going to extract the GCMF
5h(1 + 8𝑘3
)
(1)3
+ 2𝑘 2
𝑎 = 1
𝑏 = 2𝑘 𝑎3
+ 𝑏3
= (𝑎 + 𝑏)(𝑎2
− 𝑎𝑏 + 𝑏2
)
5ℎ (1)3
+ 2𝑘 3
= 5ℎ 1 + 2𝑘 12
− 1(2𝑘) + 2𝑘 2
= 𝟓𝒉 𝟏 + 𝟐𝒌 𝟏 − 𝟐𝒌 + 𝟒𝒌𝟐

12. Do:
◦Activity 2 – THE MISSING PART
◦Activity 3 – BREAK THE CUBES
Page 23