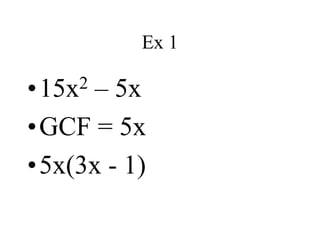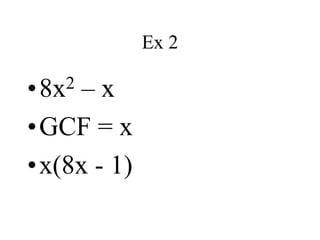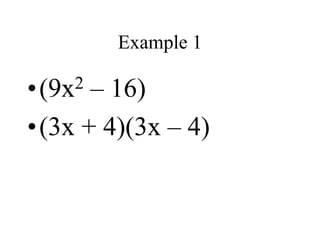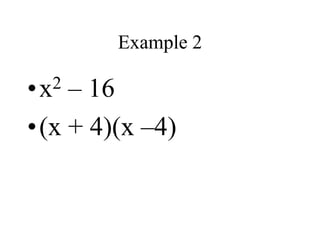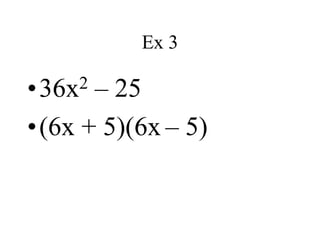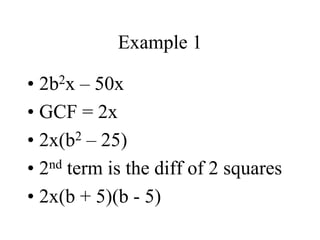This document discusses different factoring methods including the greatest common factor method and difference of two squares method. It provides examples of factoring polynomials using each method and emphasizes that the greatest common factor method should always be tried first before other factoring techniques. Students are given practice problems to factor polynomials using these methods and are reminded that sometimes a combination of factoring approaches is needed.

1. Magicians
They are all MASTERS of Magic!!

2. It is my GOAL
for each of you to become
MASTERS of
FACTORING

3. Factoring Expressions
- Greatest Common Factor
(GCF)
- Difference of 2 Squares

4. Objectives
• I can factor expressions using
the Greatest Common Factor
Method (GCF)
• I can factor expressions using
the Difference of 2 Squares
Method

5. What is Factoring?
• Quick Write: Write down everything you
know about Factoring from Algebra-1 and
Geometry?
• You can use Bullets or give examples
• 2 Minutes
• Share with partner!

6. Factoring?
• Factoring is a method to find the basic
numbers and variables that made up a
product.
• (Factor) x (Factor) = Product
• Some numbers are Prime, meaning they are
only divisible by themselves and 1

7. Method 1
• Greatest Common Factor (GCF) –
the greatest factor shared by two or
more numbers, monomials, or
polynomials
• ALWAYS try this factoring method
1st before any other method
• Divide Out the Biggest common
number/variable from each of the
terms

8. Greatest Common Factors
aka GCF’s
Find the GCF for each set of following numbers.
Find means tell what the terms have in common.
Hint: list the factors and find the greatest match.
a) 2, 6
b) -25, -40
c) 6, 18
d) 16, 32
e) 3, 8
2
-5
6
16
1
No common factors?
GCF =1

9. Find the GCF for each set of following numbers.
Hint: list the factors and find the greatest match.
a) x, x2
b) x2, x3
c) xy, x2y
d) 2x3, 8x2
e) 3x3, 6x2
f) 4x2, 5y3
x
x2
xy
2x2
Greatest Common Factors
aka GCF’s
3x2
1 No common factors?
GCF =1

10. Factor out the GCF for each polynomial:
Factor out means you need the GCF times the
remaining parts.
a) 2x + 4y
b) 5a – 5b
c) 18x – 6y
d) 2m + 6mn
e) 5x2y – 10xy
2(x + 2y)
6(3x – y)
5(a – b)
5xy(x - 2)
2m(1 + 3n)
Greatest Common Factors
aka GCF’s
How can you check?

11. FACTORING by GCF
Take out the GCF EX:
15xy2 – 10x3y + 25xy3
How:
Find what is in common
in each term and put in
front. See what is left
over.
Check answer by
distributing out.
Solution:
5xy( )
3y – 2x2 + 5y2

12. FACTORING
Take out the GCF EX:
2x4 – 8x3 + 4x2 – 6x
How:
Find what is in common
in each term and put in
front. See what is left
over.
Check answer by
distributing out.
Solution:
2x(x3 – 4x2 + 2x – 3)

13. Ex 1
•15x2 – 5x
•GCF = 5x
•5x(3x - 1)

14. Ex 2
•8x2 – x
•GCF = x
•x(8x - 1)

15. Method #2
•Difference of Two
Squares
•a2 – b2 = (a + b)(a - b)

16. What is a Perfect Square
• Any term you can take the square root
evenly (No decimal)
• 25
• 36
• 1
• x2
• y4
5
6
1
x
2
y

17. Difference of
Perfect Squares
x2 – 4 =
the answer will look like this: ( )( )
take the square root of each part:
( x 2)(x 2)
Make 1 a plus and 1 a minus:
(x + 2)(x - 2 )

18. FACTORING
Difference of Perfect
Squares
EX:
x2 – 64
How:
Take the square root of
each part. One gets a +
and one gets a -.
Check answer by FOIL.
Solution:
(x – 8)(x + 8)

19. YOUR TURN!!
Using White Boards

20. Example 1
•(9x2 – 16)
•(3x + 4)(3x – 4)

21. Example 2
•x2 – 16
•(x + 4)(x –4)

22. Ex 3
•36x2 – 25
•(6x + 5)(6x – 5)

23. More than ONE Method
• It is very possible to use more than one
factoring method in a problem
• Remember:
• ALWAYS use GCF first

24. Example 1
• 2b2x – 50x
• GCF = 2x
• 2x(b2 – 25)
• 2nd term is the diff of 2 squares
• 2x(b + 5)(b - 5)

25. Example 2
• 32x3 – 2x
• GCF = 2x
• 2x(16x2 – 1)
• 2nd term is the diff of 2 squares
• 2x(4x + 1)(4x - 1)

26. Exit Slip
• On a post it note write these 2
things: (with your name)
• 1. Define what factors are?
• 2. What did you learn today about
factoring?
• Put them on the bookshelf on the
way out!