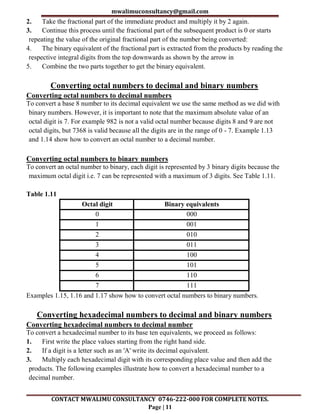
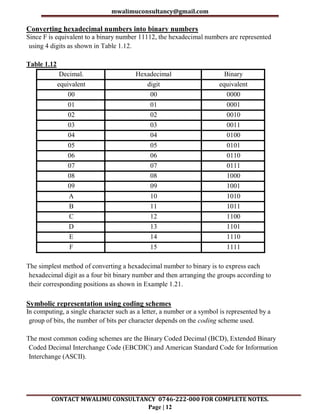
The document consists of detailed revision notes for form 3 computer studies, focusing on data representation in digital computers, including descriptions of bits, bytes, and various number systems such as binary, octal, and hexadecimal. It explains the concepts of data representation in electronic circuits, magnetic and optical media, and emphasizes the importance of binary systems due to their reliability and efficiency. Additionally, the notes provide conversion methods between different number systems and their practical applications in computing.