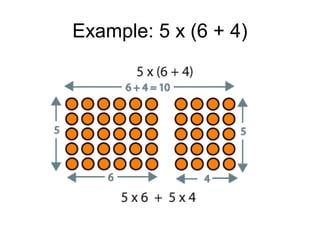
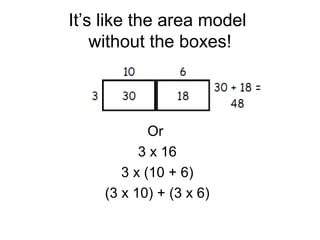
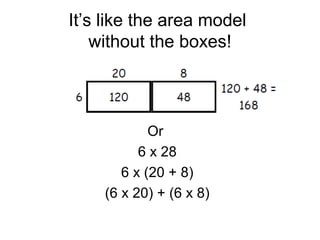
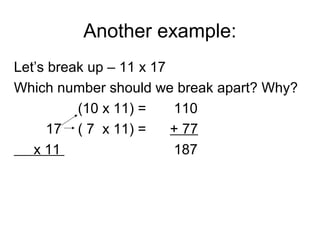The document introduces the expanded method for multiplication, which involves breaking one of the factors into parts based on place value and then distributing the other factor over the parts. Examples are provided showing how to break numbers like 10, 17, and 56 into more manageable parts before multiplying. Students are instructed to practice using the expanded method to solve multiplication problems in their journals.

1. Multiplication
with the Expanded Method
We are going to learn:
1.02c – Different multiplication strategies

2. Expanded Method– Break Apart Strategy

3. Review
• Commutative Property – Changing the
order of the factors doesn’t change the
product
• Examples?

4. Review
• Identity Property of Multiplication – Any
number times one is that same number.
• Identity Property of Addition – Any number
plus zero is that same number.
• Examples?

5. • Associative Property - Changing the
grouping of the numbers, doesn’t change
the answer.
• Remember:
8 + (9 +7) = (8 + 9) + 7
(3 x 4) x 5 = 3 x (4 x 5)

6. Let’s try something new!
• Use the expanded method to solve the
expression 5 x 10 another way…
– Distribute or share the 5 with the 6 and 4.
Check it out:
5 x 10…. Break up 10 into 6 and 4.
5 x (6 + 4) = (5 x 6) + (5 x 4)
- Solve the parentheses and then add them
together! The answer is the same.

7. Example: 5 x (6 + 4)

8. It’s like the area model
without the boxes!
Or
3 x 16
3 x (10 + 6)
(3 x 10) + (3 x 6)

9. It’s like the area model
without the boxes!
Or
6 x 28
6 x (20 + 8)
(6 x 20) + (6 x 8)

10. You find the product using the area model –
we’ll use the expanded method together.
5 x 17 9 x 73
3 x 29 8 x 156
4 x 226 7 x 305

11. Let’s Try: 20 x 56
I don’t mind multiplying with 20
because it has a zero, but 56 is
more difficult! So…
I am going to break up 56
into 50 and 6.
20 x 56 = (20 x 50) + (20 x 6)

12. Another example:
Let’s break up – 11 x 17
Which number should we break apart? Why?
(10 x 11) = 110
17 ( 7 x 11) = + 77
x 11 187

13. 36 x 22

14. Expanded Method
(Distributive Property)
24 x 55
1. Pick one of the numbers to break apart 24
2. Break it apart by:
the value of the tens place – 20
the value of the ones place – 4.
3. Multiply each piece x the second number – 55.
(20 x 55) + (4 x 55)
4. Add the products together.

15. • Now – you try some examples in your
journal.

16. • Solve the following problems by the breaking
apart the underlined number.
47 x 30 63 x 41
12 x 52 23 x 29

17. 23 x 29
Player A – Area Model
Player B – Distributive Property
(20 x 29) + (3 x 29)
Player C – Calculator =
Player D – 20 x 30 = 600