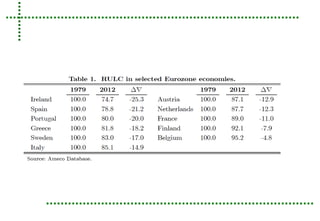
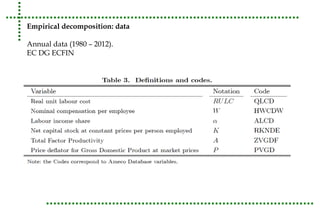
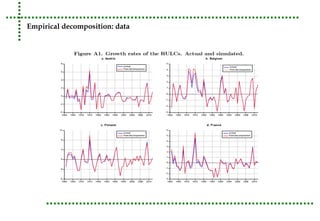
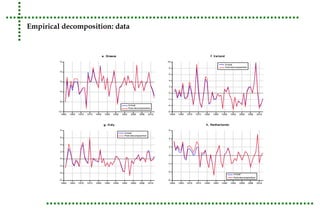
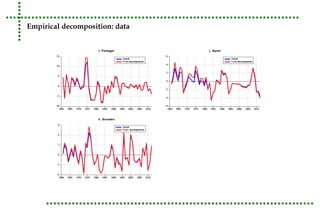
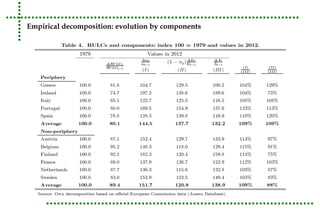
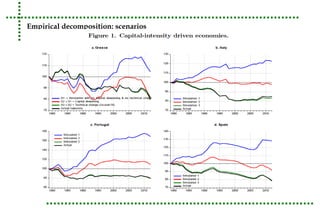
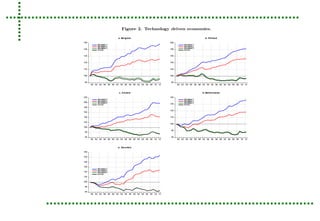
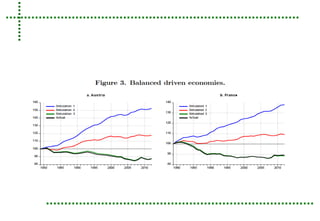
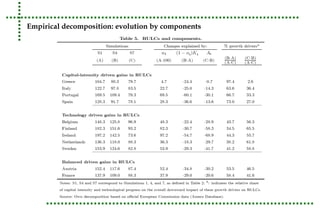
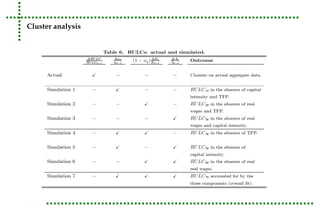
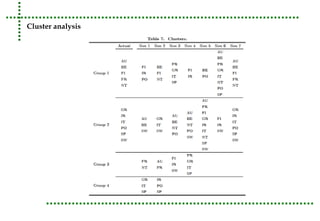
This document analyzes real unit labor costs (RULC) in 11 Eurozone countries from 1980 to 2012 to examine divergence forces. RULC is decomposed into components including labor productivity and nominal compensation per employee. A cluster analysis is performed using the Phillips and Sul methodology to test for convergence or divergence among the countries. The analysis finds that countries can be grouped into clusters based on their RULC performance, indicating latent divergence forces rather than overall convergence across the Eurozone. Internal devaluation policies are deemed insufficient and technology differences are identified as the main driver of observed divergences.

1. Eesti Pank
June 18, 2014
Real unit labour costs in Eurozone countries:
Drivers and clusters
Javier Ordóñez
Hector Sala
José I. Silva

2. Introduction:
Can nominal convergence last in the absence of real convergence?
Our view is that the EU policy mix has been successful in terms of nominal
convergence but has not been conducive to overall growth nor to real convergence
across the euro area.
The current economic crisis is the consequence of differences in competitiveness that
generate real divergence and, therefore, growing account imbalances.
In this paper we take the real unit labour cost (RULC) as a relevant indicator of
competitiveness and, as such, as a driver of real convergence. We examine to what
extent our hypothesis of latent divergence forces holds by clustering the RULC
according to its performance in a selection of 11 Eurozone economies.

4. Analytical decomposition:
RULC can be defined as:
Or alternatively,
(1)
Output per employee can be expressed as:
(2)

5. Inserting (2) in (1) and differentiating we get:

6. Empirical decomposition: data
Annual data (1980 – 2012).
EC DG ECFIN

7. Empirical decomposition: data

8. Empirical decomposition: data

9. Empirical decomposition: data

10. Empirical decomposition: evolution by components

11. Empirical decomposition: scenarios

14. Empirical decomposition: evolution by components

15. Cluster analysis: methodology
To test for clusters we use the Phillips and Sul (2007, 2009) methodology.
These authors decomposed the variable of interest in two components, one common,
one idyosincratic, both of which are time varying:
The time varying representation in can be used to separate common from
idiosyncratic components in the traditional decomposition of panel data:
where git embodies systematic components, including permanent components that
give rise to cross section dependence, and ait represents a transitory component.

16. Cluster analysis: methodology
This simple econometric representation can be used to analyze growth convergence
by testing whether the factor loadings converge.
Phillips and Sul (2009) proposed a modification of the neoclassical growth model so
that technological growth rates differ across and over time and are endogenously
determined.
To account for temporal and transitional heterogeneity, Phillips and Sul (2009)
introduced time-heterogeneous technology by allowing technological progress, ,
to follow a path of the form

17. Cluster analysis: methodology
Under this heterogeneous technology the individual transition path of log per capita
real income evolves as:
is the initial level of log per capita real income
is the steady-state level of log per capita real income
is the time-varying spped of adjustment

18. Cluster analysis: methodology
This equation can be expressed in form of the time-varying representation:
This dynamic factor formulation involves:
1.A growth component common across countries (represents commonly available
world technology such as the industrial an scientific revolution and internet
technology).
2.An individual transition factor which measures the transition path of a economy to
the common steady-state growth path, μ
During transition depends on:
1.The speed of adjustment of convergence parameter, βit
2.The rate of technological progress, xit
3.And the initial endowment and steady-state level through the parameter ait

19. Cluster analysis: methodology
Phillips and Sul (2007) proposed to model the transition elements by the
construction of a relative measure of the transition coefficients:
Next, these authors construct a cross-sectional mean square transition differential,
where

20. Cluster analysis: methodology
To formulate a null hypothesis of growth convergence, the authors proposed the
following model for the transitions elements:
where:
δi is fixed
σi > 0
ξit is i.i.d(0,1) across i bay weakly dependent on t (introduces time-vaying and region-specific
components to the model)
L(t) is a slowly varying function which tend to infinity as t does (in practice log t)
α determines the beahviour (convergence or divergence) of

21. Cluster analysis: methodology
The null hypothesis of convergence can be written as:
and the alternative (divergence):
or club convergence:

22. Cluster analysis: methodology
Phillips and Sul (2007) show that these hypothesis can be statistically tested by means
of the following ‘log t’ regression model:
Advantages of this approach:
1.It is a test for relative convergence as it measures convergence to some cross
sectional average in contrast to the concept of level convergence analyzed by Bernard
and Durlauf (1995).
2.This test does not depend on any particular assumption concerning trend
stationarity or stochastic nonstationarity of the variables to be tested.

23. Cluster analysis

24. Cluster analysis

25. Concluding remarks
Since the oberved divergencies can be ascribed mainly to different technological
levels, rather than to a wrong wage behaviour in the Periphery, internal devaluation
policies are not the solution to surpass the current situation in the Eurozone. These
policies have forced rebalancing of the external deficits, but they do not help
convergence. And the reason is the same we have heard many times when economies
embark in external devaluations: these are not genuine competitive gains, it is
technology what matters.
Hence, looking retrospectively, the definition of the Maastricht criteria should have
been probably more balanced towards the inclusion of some real convergence
indicators to be fulfilled before joining the EMU. The extensive battery of indicators
considered in the macroeconomic imbalance procedure (MIP) constitute a response
to this void. We cannot abstain, however, to point out that this new set of indicative
thresholds are formulated as a surveillance mechanism, and not as convergence
targets. We wonder, in the current context, whether some real convergence indicators
should also be targeted to safeguard, or at least strengthen, the process of European
integration.