Download to read offline
Uploaded byNoor Izwan Abd Rahim
entah la
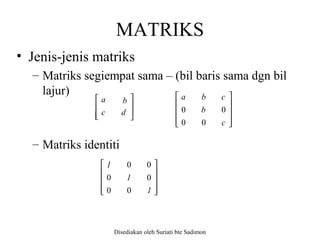
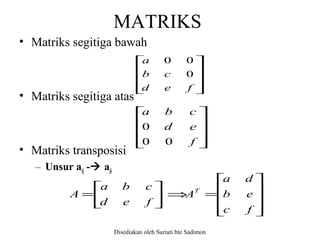
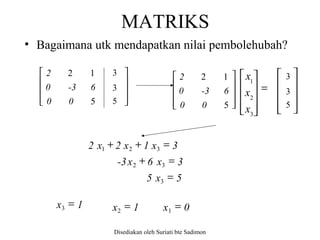
Dokumen menerangkan pelbagai jenis persamaan linear dan bagaimana sistem persamaan linear terdiri daripada lebih satu persamaan. Penyelesaian sistem ini boleh menghasilkan penyelesaian unik, tidak unik, atau tiada penyelesaian, bergantung kepada perhubungan antara garis. Selain itu, ia menjelaskan tentang matriks, jenis-jenisnya, serta kaedah untuk menyelesaikan sistem persamaan linear dengan menggunakan pelbagai teknik seperti penghapusan gauss dan kaedah iteratif.
entah la
- 1. Disediakan oleh Suriatibte Sadimon SISTEM PERSAMAAN LINEAR
- 2. Disediakan oleh Suriatibte Sadimon PERSAMAAN LINEAR • 2 jenis • 1. Persamaan pada satah – y=mx +c atau ax +by = c • 2. Persamaan dalam ruang – ax + by +cz = d • Sistem persamaan linear – Lebih daripada satu persamaan – a1x + b1y = c1 dan a2x + b2y = c2 – Atau – a1x + b1y + c1z = d1 , a2x + b2y + c2z= d2, – a3x + b3y + c3z = d3
- 3. Disediakan oleh Suriatibte Sadimon Penyelesaian sistem persamaan linear • Dapatkan nilai pembolehubah • 3 kemungkinan – Garis bersilang penyelesaian unik – Garis bertindih penyelesaian tidak unik – lebih daripada satu nilai – Garis selari tiada penyelesaian
- 4. Disediakan oleh Suriatibte Sadimon Penyelesaian sistem persamaan linear • Penyelesaian persamaan linear melibatkan penyelesaian matriks • tukarkan sistem persamaan linear kpd bentuk matriks • Umumnya btk matriks Ax = B – A => matriks pekali , x => vektor penyelesaian dan b => vektor lajur 22212 12111 cxbxa cxbxa =+ =+ = 2 1 2 1 22 11 c c x x ba ba 3332313 2322212 1312111 dxcxbxa dxcxbxa dxcxbxa =++ =++ =++ = 3 2 1 3 2 1 333 222 111 d d d x x x cba cba cba
- 5. Disediakan oleh Suriatibte Sadimon MATRIKS • Jenis-jenis matriks – Matriks segiempat sama – (bil baris sama dgn bil lajur) – Matriks identiti 1 1 1 00 00 00 c b a 00 00 cb d a c b
- 6. Disediakan oleh Suriatibte Sadimon MATRIKS • Matriks segitiga bawah • Matriks segitiga atas • Matriks transposisi – Unsur aij - aji fed cb a 0 00 f ed cba 00 0 =⇒ = fc eb da A fed cba A T
- 7. Disediakan oleh Suriatibte Sadimon MATRIKS • Matriks simetri A = AT • Matriks songsangan A-1 – AB = BA = I (matrik identiti) – A ialah matriks songsangan bagi B dan B ialah matrik songsangan bagi A – Disimbolkan A-1 dan B -1 – A-1 A = I =⇒ = 124 212 421 124 212 421 T AA
- 8. Disediakan oleh Suriatibte Sadimon MATRIKS • Penentu (determinant) |A| – A = – |A| = ad – bc • Sistem persamaan linear mempunyai penyelesaian unik jika – Merupakan matriks segiempat sama – Nilai |A|≠ 0 – Wujud Songsangan matriks A -1 d a c b
- 9. Disediakan oleh Suriatibte Sadimon MATRIKS • Bagaimana menukarkan persamaan linear ke bentuk matriks imbuhan? • Contoh = 2 1 2 1 22 11 c c x x ba ba 22212 12111 cxbxa cxbxa =+ =+ 22 11 ba ba c c 2 1 321 321 321 2x4x-2x1 1x2x-1x-1 3x1x2x2 =++ =++ =++
- 10. Disediakan oleh Suriatibte Sadimon MATRIKS • Operasi baris permulaan – Mendarabkan sebarang baris matriks dgn satu pemalar – Menambahkan satu persamaan dgn persamaan lain yang digandakan – Saling tukarkan baris persamaan matriks
- 11. Disediakan oleh Suriatibte Sadimon MATRIKS • Contoh: • Tukarkan matriks imbuhan berikut ke bentuk matriks segitiga atas menggunakan operasi baris permulaan 4-21 -1-1 2 2 12 3 1 2 33 2322 131211 00 0 u uu uuu d1 d2 d3
- 12. Disediakan oleh Suriatibte Sadimon MATRIKS 4-21 -1-1 2 2 12 3 1 2 Penyelesaian: B3 = B3 + B2 6-30 -1-1 2 2 12 3 1 3 B2 = B2*2 6-30 -2-2 2 4 12 3 2 3 6-30 00 2 5 12 3 5 3 B2 = B2+B1 6-30 2 12 3 3 B2 B3 00 5 5
- 13. Disediakan oleh Suriatibte Sadimon MATRIKS • Bagaimana utk mendapatkan nilai pembolehubah? 6-30 2 12 3 3 00 5 5 6-30 2 12 3 3 00 5 5 = 3 2 1 x x x 3 32 321 5x5 3x6x-3 3x1x2x2 = =+ =++ 3 1x = 2 1x = 1 0x =
- 14. Disediakan oleh Suriatibte Sadimon Kaedah Penyelesaian Sistem Persamaan Linear 1. Kaedah Langsung 1.1 Kaedah Penghapusan Gauss 1.2 Kaedah Penghapusan Gauss Jordan 1.3 Kaedah Pemfaktoran Doolittle 1.4 Kaedah Pemfaktoran Crout 1. Kaedah Lelaran (tak langsung) 2.1 Kaedah lelaran Jacobi 2.2 Kaedah Lelaran Gauss-Seidel