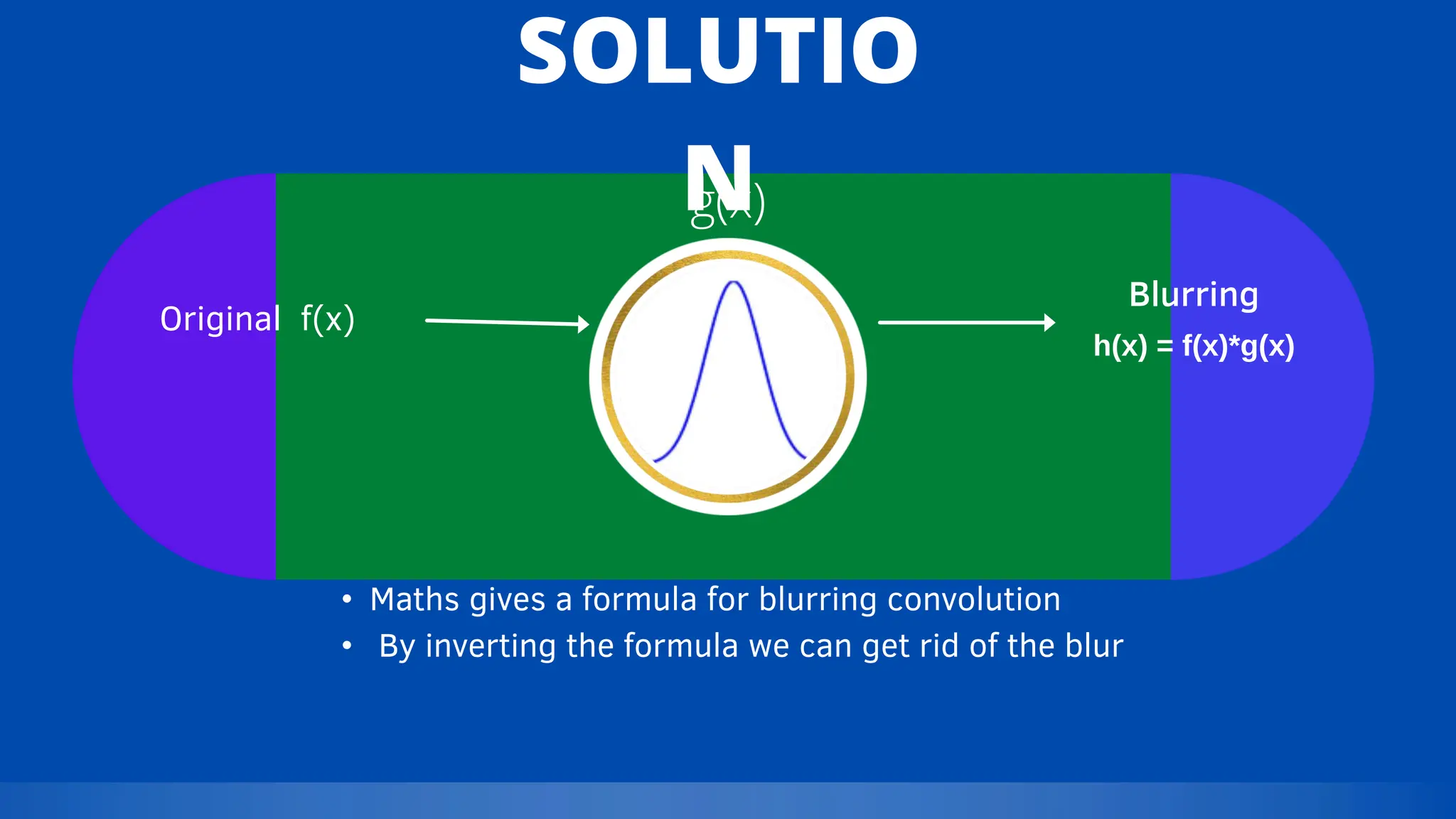
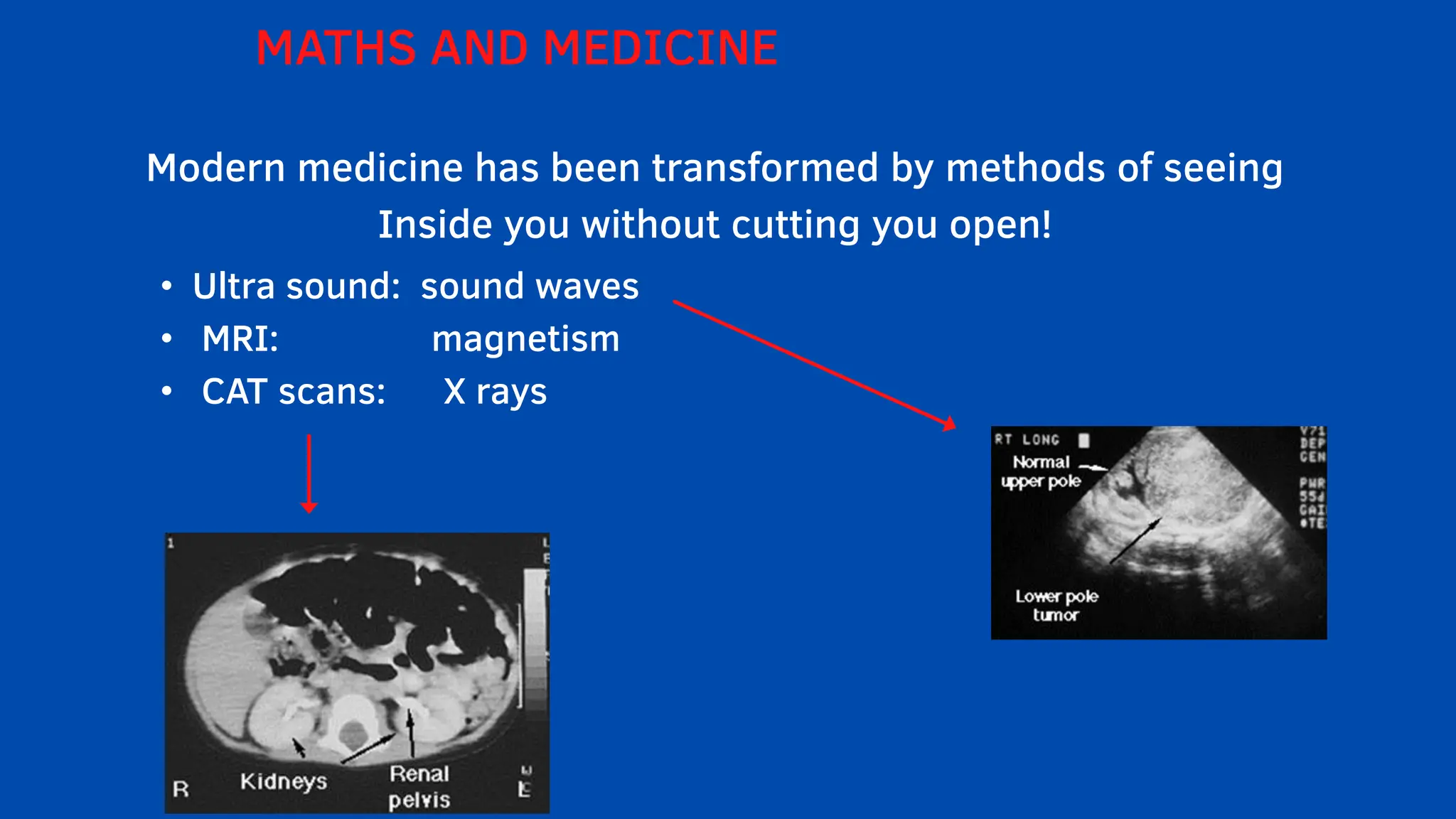
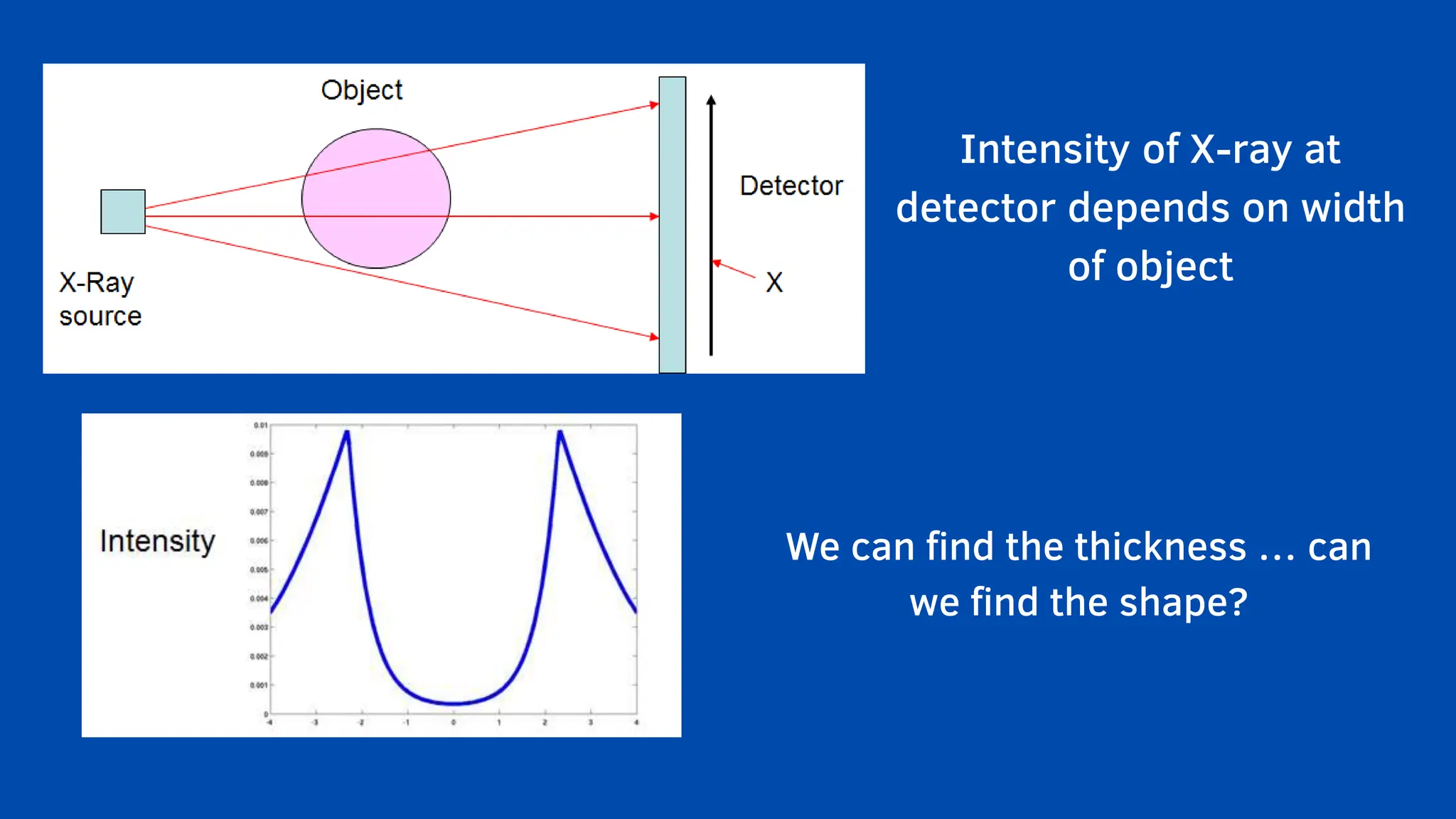
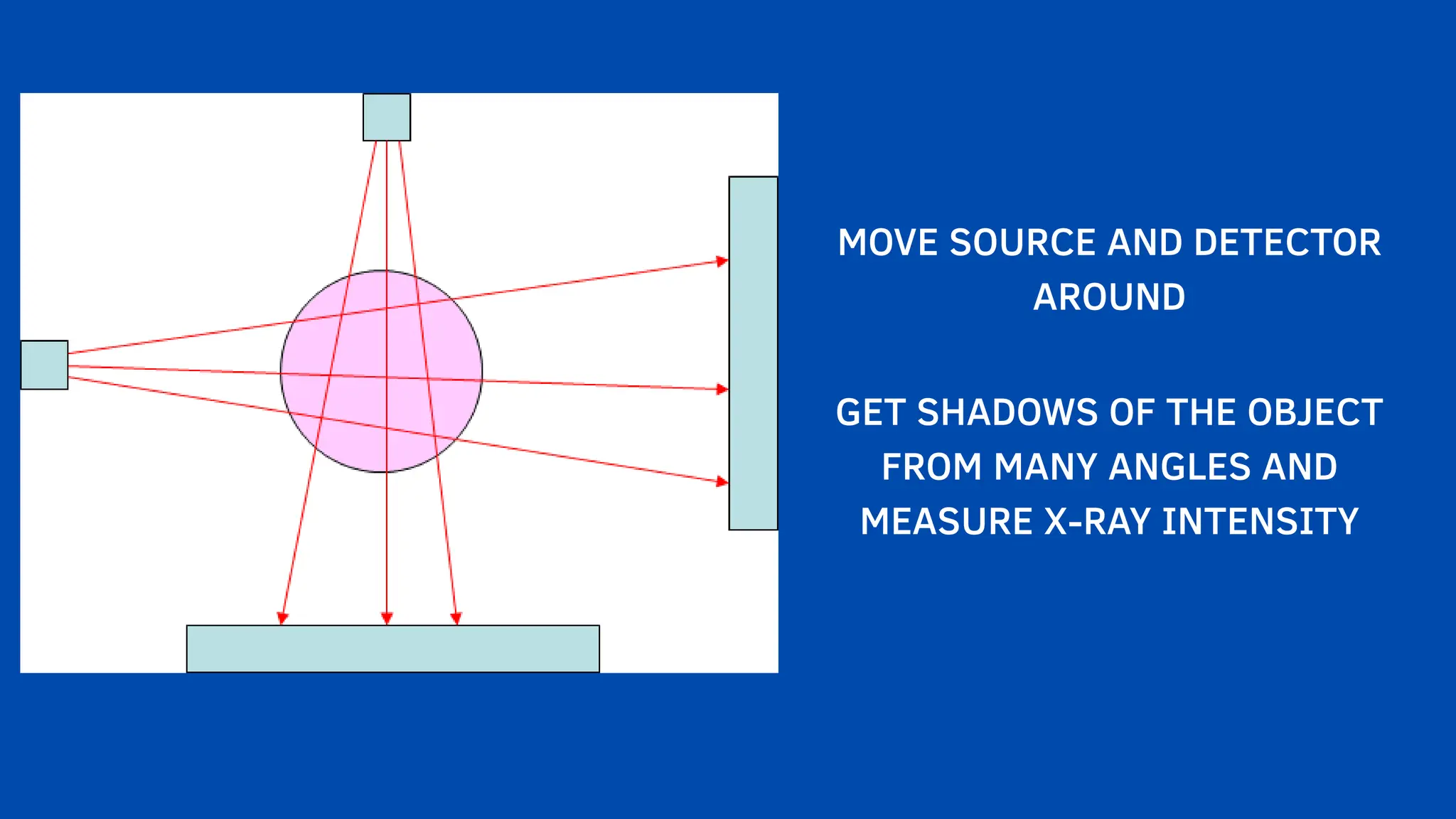
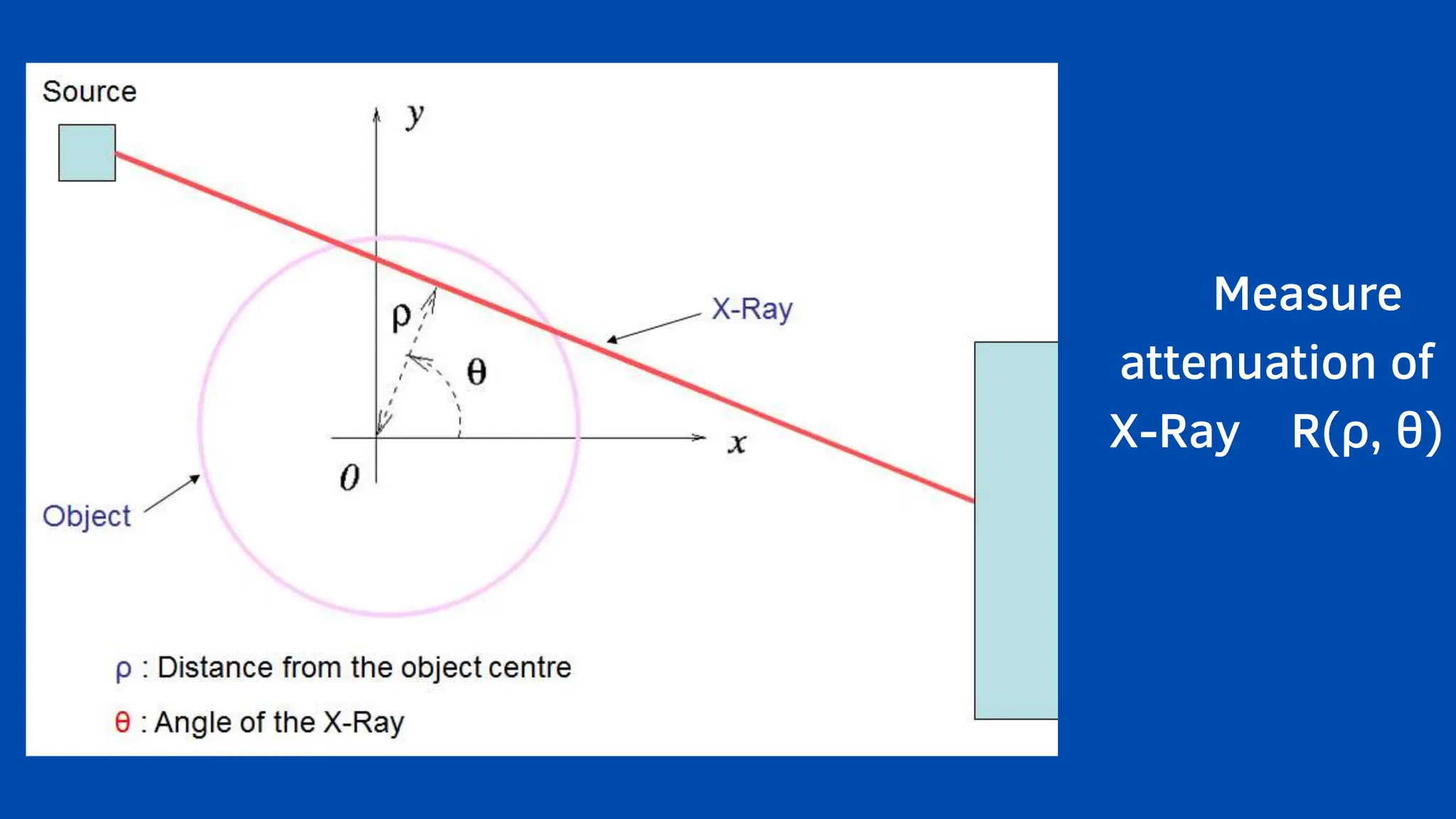
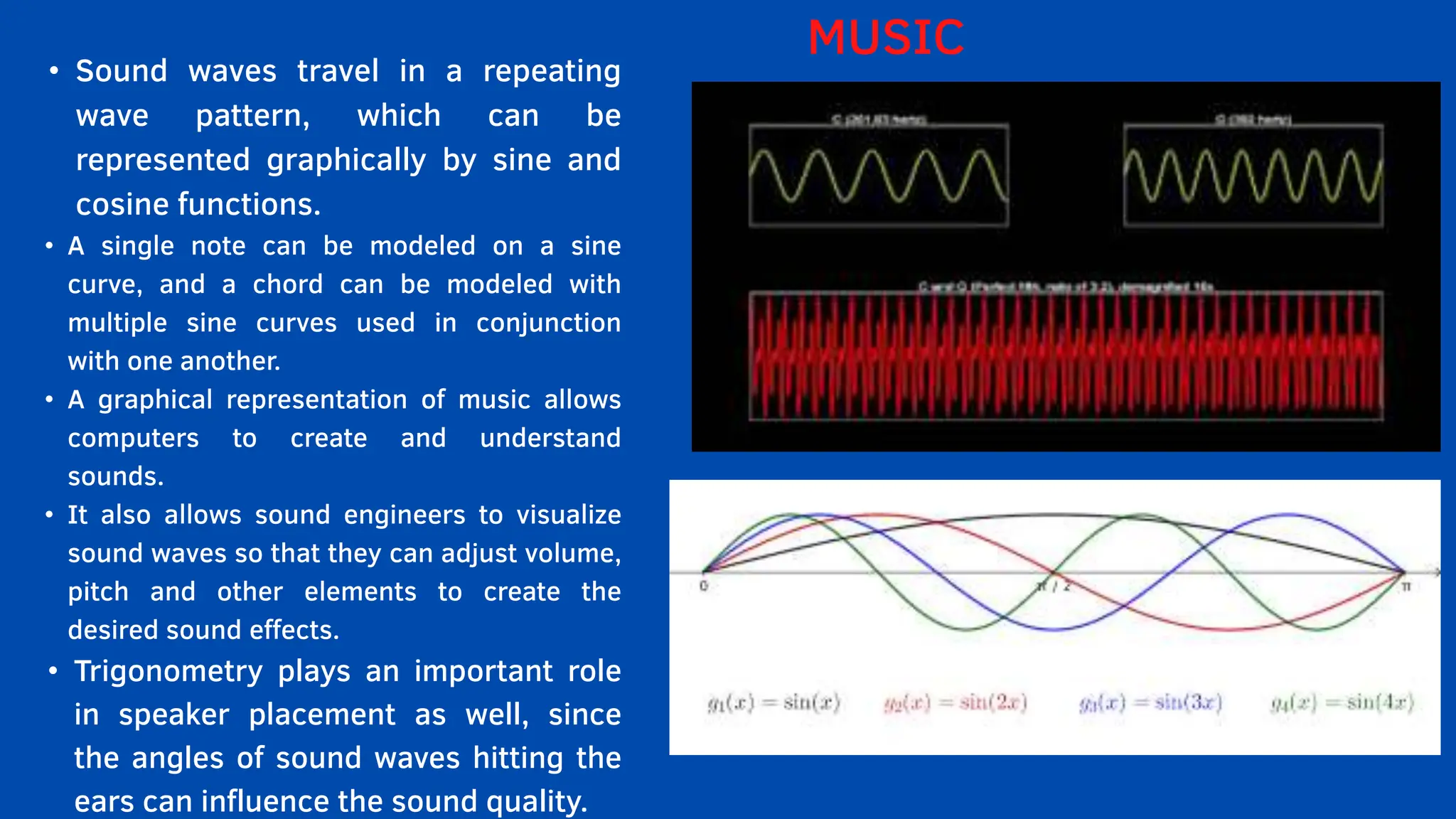
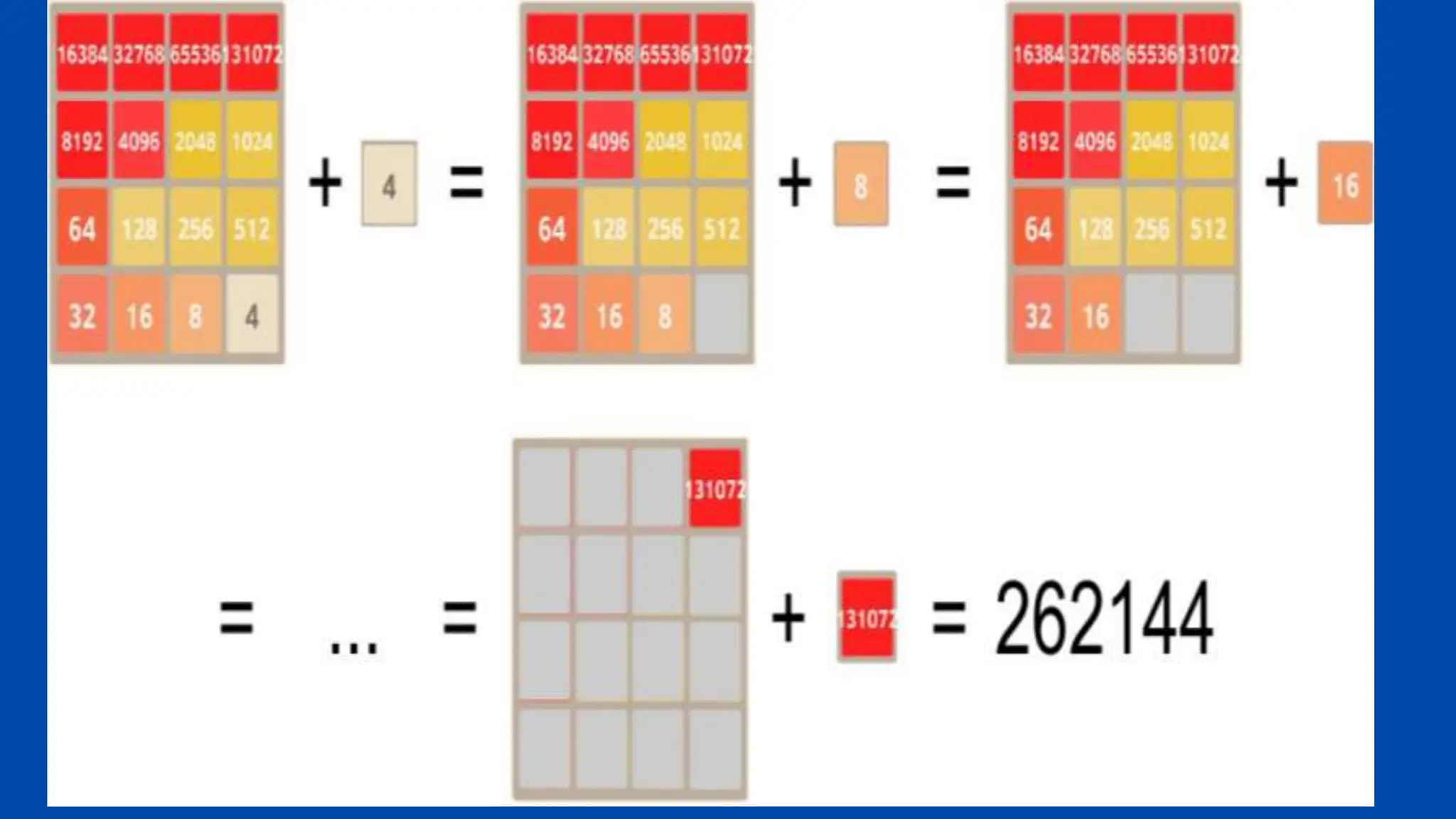
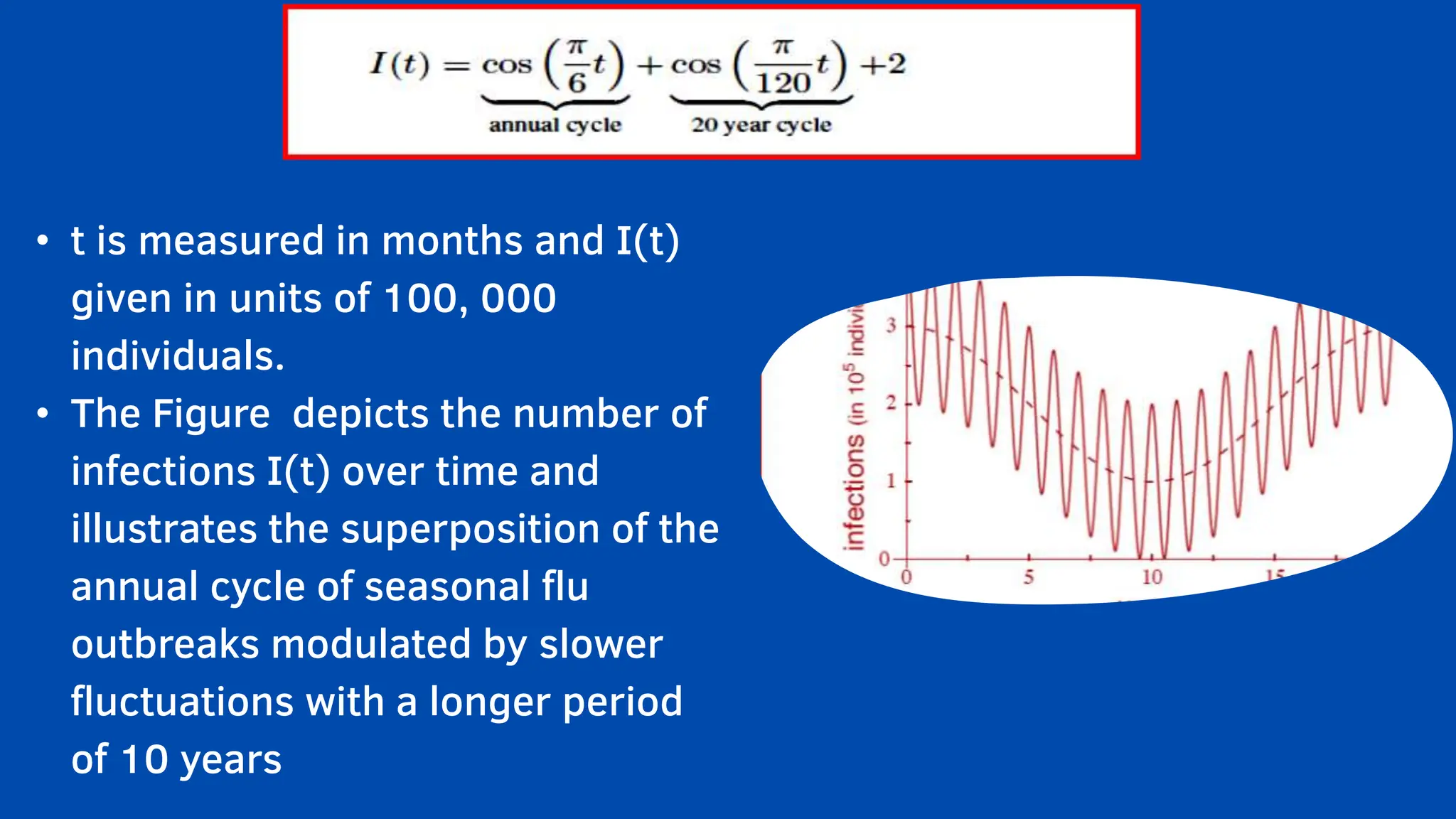
The document emphasizes the critical role mathematics plays in various aspects of everyday life, from simple calculations in cooking and travel to complex applications in medicine and engineering. It highlights how mathematical understanding enhances decision-making, problem-solving skills, and is essential across multiple fields such as medicine, crime detection, and interior design. Ultimately, the text argues that neglecting mathematics hinders knowledge and everyday functionality, underlining its significance in both personal and professional contexts.

1. M.K. TAMIL SELVI
HOD, MATHS
Alpha College of Engineering

2. Mathematics is the gate and key of the
sciences... Neglect of mathematics works
injury to all knowledge , since he who is
ignorant of it cannot know the other
sciences or the things of this world. And
what is worse, men who are thus Ignorant
are unable to perceive their own
ignorance and so do not seek a remedy.
Roger
Bacon

3. At Home
• Setting an alarm and hitting snooze, they may quickly need
to calculate the new time they will arise.
• Or they might step on a bathroom scale and decide that
they’ll skip those extra calories at lunch.
• People on medication need to understand different dosages,
whether in grams or milliliters.
• Recipes call for ounces and cups and teaspoons --all
measurements, all math.
• And decorators need to know that the dimensions of their
furnishings and rugs will match the area of their rooms.

4. In Travel
• Travelers often consider their miles-per-gallon when fueling up for daily trips, but they might need to calculate anew when faced with obstructionist
detours and consider the cost in miles, time and money.
• Air travelers need to know departure times and arrival schedules. They also need to know the weight of their luggage unless they want to risk some
hefty baggage surcharges.
• Once on board, they might enjoy some common aviation-related math such as speed, altitude and flying time.

5. SOME COMMON VIEWS OF
MATHEMATICS
• MATHS IS HARD
• MATHS IS BORING
• MATHS HAS NOTHING TO DO WITH
REAL LIFE
• ALL MATHEMATICIANS ARE MAD!
BUT I CAN SHOW YOU THAT MATHS
IS IMPORTANT IN
CRIME DETECTION, MEDICINE
and ......

6. • Balancing the checkbook.
• Understanding loans for various purposes.
• Understanding sports
• Managing money.
• Shopping for the best price.
• Figuring out time, distance, and cost for travel.
• Playing music.
• Gardening and landscaping.
There are several
concepts that include
maths, such as
weighing,
understanding
chemical formulas,
analyzing marketing
data, measuring,
drafting, and
calculating statistics.

7. • The population of a village
increases continuously at the
rate proportional to the number
of its inhabitants present at any
time.
• If the population of the village
was 20, 000 in 1999 and 25000
in the year 2004, what will be
the population of the village in
2009?
• It can be solved quickly using
differential equations
BIRTH

8. • Temperature of a dead
body at 11:30 pm was
94.6 F.
• Temperature of the body
again after one hour , which
was 93.4 F.
• If the temperature of the
room was 70 F, estimate the
time of death.
• Taking normal temperature
of body as 98.6 F.
• This also can be solved
using differential equations.
DEATH

9. MATHS AND CRIME
A short mathematical story
• Burglar robs a bank
• Escapes in getaway
car
• Pursued by police
• GOOD NEWS Police take a photo
• BAD NEWS Photo is blurred

10. Original
Blurred

11. Original f(x)
g(x)
Blurring
h(x) = f(x)*g(x)
SOLUTIO
N
• Maths gives a formula for blurring convolution
• By inverting the formula we can get rid of the blur

13. Modern medicine has been transformed by methods of seeing
Inside you without cutting you open!
MATHS AND MEDICINE
• Ultra sound: sound waves
• MRI: magnetism
• CAT scans: X rays

14. WHAT IS A CAT SCAN??
CAT = Computerised axial tomography
Based on X-Rays discovered by Roengten
• X-Rays cast a shadow
• GOOD for looking at bones
• BAD for looking at soft tissue

15. USING MODERN MATHS WE
CAN DO A LOT BETTER
Modern CAT scanner
CAT scanners work by
casting many shadows
with X-rays and using
maths to assemble these
into a picture

16. Intensity of X-ray at
detector depends on width
of object
We can find the thickness … can
we find the shape?

17. MOVE SOURCE AND DETECTOR
AROUND
GET SHADOWS OF THE OBJECT
FROM MANY ANGLES AND
MEASURE X-RAY INTENSITY

18. Measure
attenuation of
X-Ray R(ρ, θ)

19. • The study of the art
involves the study of
geometry; therefore, the
students who have
knowledge of basic
geometry formulas can
easily craft impressive art
features.
• Also, each photographer
uses mathematics to
measure the focal length,
exposure time, shutter
speed, and lighting angles
to take the photos.
ARTS

20. • Sound waves travel in a repeating
wave pattern, which can be
represented graphically by sine and
cosine functions.
• A single note can be modeled on a sine
curve, and a chord can be modeled with
multiple sine curves used in conjunction
with one another.
• A graphical representation of music allows
computers to create and understand
sounds.
• It also allows sound engineers to visualize
sound waves so that they can adjust volume,
pitch and other elements to create the
desired sound effects.
• Trigonometry plays an important role
in speaker placement as well, since
the angles of sound waves hitting the
ears can influence the sound quality.
MUSIC

21. CRIMINOLOGY – Blood Stain Analysis

22. • To find out how light levels
at different depths affect
the ability of algae to
photosynthesize.
• Trigonometry is used in
finding the distance
between celestial bodies.
• Utilize mathematical
models to measure and
understand sea animals
and their behaviour.
• Marine biologists may use
trigonometry to determine
the size of wild animals
from a distance.
MARINE

23. APPLICATIONS IN ENGINEERING
If you know the distance from where you
observe the building and the angle of
elevation you can easily find the height of
the building. Similarly, if you have the value
of one side and the angle of depression
from the top of the building you can find
and another side in the triangle, all you
need to know is one side and angle of the
triangle.

24. APPLICATIONS IN ENGINEERING
Game, Mario.
When you see him so smoothly glide over the road
blocks.
He doesn’t really jump straight along the Y axis,
It is a slightly curved path or a parabolic path that
he takes to tackle the obstacles on his way.
Trigonometry helps Mario jump over these
obstacles.
Gaming industry is all about IT and computers
and hence Trigonometry is of equal importance
for these engineers.

25. APPLICATIONS IN ENGINEERING
• Flight engineers have to take in
account their speed, distance, and
direction along with the speed and
direction of the wind.
• The wind plays an important role in
how and when a plane will arrive
where ever needed this is solved
using vectors to create a triangle
using trigonometry to solve.
• Trigonometry will help to solve for
that third side of your triangle
which will lead the plane in the
right direction, the plane will
actually travel with the force of
wind added on to its course.

26. • Consider problem of a substance
dissolved in a liquid.
• The liquid entering the tank may or
may not contain more of the
substance dissolved in it.
• Liquid leaving the tank will contain
the substance dissolved in it.
• If Q(t) gives the amount of the
substance dissolved in the liquid in
the tank at any time t
• To develop a differential equation,
when solved, will give us an
expression for Q(t).
MIXING
PROBLEMS
Assumption:
Concentration
of
the
substance
in
the
liquid
is
uniform
throughout
the
tank.

27. The main “equation” for this model

28. • A 1500 gallon tank initially
contains 600 gallons of water
with 5 lbs of salt dissolved in
it. Water enters the tank at a
rate of 9 gal/hr and the water
entering the tank has a salt
concentration of
15(1+cos(t)) lbs/galI. If a
well mixed solution leaves
the tank at a rate of 6 gal/hr,
how much salt is in the tank
when it overflows?
MIXING
PROBLEMS

29. • Assume a uniform concentration of salt in the tank.
• The concentration at any point in the tank and hence in the
water exiting is given by,
• 𝐶𝑜𝑛𝑐𝑒𝑛𝑡𝑟𝑎𝑡𝑖𝑜𝑛= (𝐴𝑚𝑜𝑢𝑛𝑡 𝑜𝑓 𝑠𝑎𝑙𝑡 𝑖𝑛 𝑡ℎ𝑒 𝑡𝑎𝑛𝑘 𝑎𝑡 𝑎𝑛𝑦 𝑡𝑖𝑚𝑒 𝑡,)/(
𝑉𝑜𝑙𝑢𝑚𝑒 𝑜𝑓 𝑤𝑎𝑡𝑒𝑟 𝑖𝑛 𝑡ℎ𝑒 𝑡𝑎𝑛𝑘 𝑎𝑡 𝑎𝑛𝑦 𝑡𝑖𝑚𝑒, 𝑡)
• The amount of salt at any time t is Q(t).
• Let the initial volume be 600 gallons
• Every hour 9 gallons enter and 6 gallons leave.
• At any time t there is 600+3t gallons of water in the tank.

30. • An apple pie with an initial temperature of 170 C is
removed from the oven and left to cool in a room with
an air temperature of 20 C. Given that the temperature
of the pie initially decreases at a rate of 3:0 C=min,
how long will it take for the pie to cool to a
temperature of 30 C?
• Assuming the pie obeys Newton's law of cooling, we
have the following information:
• 𝑑𝑇/𝑑𝑡=−𝑘(𝑇−20), T(0) = 170; T’(0) = -3:0;
• where T is the temperature of the pie in celsius, t is the
time in minutes, and k is an unknown constant.
• ∫1𝑑𝑇/(𝑇−20)=−∫𝑘𝑑𝑡 ⟹ ln|𝑇−20|=−𝑘𝑇+𝐶. 𝑎𝑛𝑑 𝑇
=20+𝐶𝑒^(−𝑘𝑡) 〗
• Solving,
• 𝑇=20+150𝑒^(−0,02𝑡)
COOKING

31. The Math of Social Distancing Is a Lesson in Geometry
Determining how to safely reopen
buildings and public spaces under
social distancing is in part an exercise
in geometry: If each person must keep
six feet away from everyone else, then
figuring out how many people can sit in
a classroom or a dining room is a
question about packing non-
overlapping circles into floor plans.

32. • Fibonacci numbers
occur in nature in
many places.
Petals of flowers are
an example
• While individual
examples may
disagree, the most
common number of
petals are usually
close to Fibonacci
numbers
Mathematics determined the
symmetry, the harmony, the
eye's pleasure.
FIBONACCI
NUMBERS

33. • When you count the number of petals of flowers in
your garden, you will get the numbers 3, 5, 8,13, 21,
34, or 55.
• These numbers are not random numbers.
• These are very unique numbers and all of them part
of Fibonacci sequence, which are series of numbers
developed by a 13th century mathematician.
• You can also get the same numbers if you start with
the numbers 1 and 1.
• And from that point on you keep adding up the last
two numbers. 1+1 = 2, 1+2 = 3, 2+3 = 5, 3+5=8
and you keep going like this.
• You will get the number of the petals of flowers.

34. • Geometric sequences have a
domain of only natural numbers
(1,2,3,...), and a graph of them
would be only points and not a
continuous curved line.
• The best one is tile values in the
game 2048.
• tile 1 = 2
• tile 2 = 4
• tile 3 = 8
• tile 4 = 16
• tile 5 = 32
• tile 6 = 64
• And so on
GAME
2048

35. • Compute the sum of all tiles
• Easy…… That’s 4+8+16+…+131,072, right?
• As a lazy mathematician, I don’t like doing long additions… So let me
show you a trick to easily compute the sum of this all.
• Let me add 4 to the sum 4+8+16+…+131,072 By combining 4 with
our tile 4, we obtain a new tile 8. But then, this new tile 8 can be
combined with the existing tile 8, hence creating a new tile 16… And
so on.
• Amazingly, our computation simplifies to the simple addition
131,072+131,072. Now add 4 to 4+8+16+…+131,072 to obtain that
number.
• So to determine 4+8+16+…+131,072 we merely need to subtract 4
to the computation we did above, hence obtaining
• 4+8+16+…+131,072=(131,072+131,072)-4=262,140
• How awesome is that?
Geometric Sums in 2048

37. • Waw! That’s magical! But where does that come
from?
• It’s the magic of so-called geometric sums. Our
geometric sum is
• 2^2+2^3+2^4+…+2^17 and we have the crucial
property 2^𝑘+2^𝑘=2^(𝑘+1)
• So, by adding 2^2, we have
• 2^2+ (2^2+ 2^3+2^4+…+2^17 )
• =(2^2+2^2 )+( 2^3+2^4+…+2^17 )
• = 2^3 +〖(2〗^3+2^4+…+2^17)

38. • The Health Canada has been monitoring
flu outbreaks continuously over the last
100 years. They have found that the
number of infections follows an annual
(seasonal) cycle and a twenty-year-cycle.
In all, the number of infections I(t) are
well-approximated by the function:
FLU-VACCINATION

39. • t is measured in months and I(t)
given in units of 100, 000
individuals.
• The Figure depicts the number of
infections I(t) over time and
illustrates the superposition of the
annual cycle of seasonal flu
outbreaks modulated by slower
fluctuations with a longer period
of 10 years

40. The minimum of the 5-year average by solving (𝑑𝐼 ̅(𝑡))/𝑑𝑡=0

41. • Note, we have used the
trigonometric identity
cos(α+β)=cos αcosβ-sinαsinβ
• Hence, the start of a 5-year
minimum (or maximum) average
period is marked by the condition
• 𝑐𝑜𝑠(𝜋/120 𝑡)=−𝑠𝑖𝑛(𝜋/120 𝑡).
• Now cos α = -sin α holds for 𝛼
=3𝜋/4 and 𝛼=7𝜋/4
• (as well as when adding multiples
of 2π to α).
• Since cos(α) is a decreasing
function for 0 < α < π, we expect
that 𝛼=3𝜋/4 marks a minimum.
𝜋/120 𝑡=3𝜋/4. Yields t=90 months.
Indeed, this indicates
the start of a 5-year
minimum average
because
├ (𝑑^2 𝐼 ̅(𝑡))/〖𝑑𝑡〗^2 ┤|_(𝑡=90)=𝜋
/120>0.
Hence the earliest intervention
could start on June 1st , 2020.

43. Mathematics puzzles,
games,
Government and military
organization websites
Financial information like
credit card number and
bank account,
Information security, all
related encode, decode,
theory
MATRICES

44. For cooking or baking anything, a
series of steps are followed,
telling us how much of the
quantity to be used for cooking,
the proportion of different
ingredients, methods of cooking,
the cookware to be used, and
many more. Such are based on
different mathematical concepts.
Indulging children in the kitchen
while cooking anything, is a fun
way to explain maths as well as
basic cooking methods.
Maths in kitchen

45. MATHS
in sports
• Maths improves the
cognitive and decision-
making skills of a person.
• Such skills are very
important for a sportsperson
because by this he can take
the right decisions for his
team.
• If a person lacks such
abilities, he won’t be able to
make correct estimations.
• So, maths also forms an
important part of the sports
field.

46. Management of Time
Now managing time is one of the most
difficult tasks which is faced by a lot of
people. An individual wants to complete
several assignments in a limited time. Not
only the management, some people are not
even able to read the timings on an analog
clock. Such problems can be solved only by
understanding the basic concepts of maths.
Maths not only helps us to understand the
management of time but also to value it.
• Logical Reasoning
• Basic Mathematical Operations
• Reasoning

47. Maths is the basis of any construction
work. A lot of calculations, preparations
of budgets, setting targets, estimating
the cost, etc., are all done based on
maths. If you don’t believe, ask any
contractor or construction worker, and
they will explain as to how important
maths is for carrying out all the
construction work.
In Construction Preparing budgets
Estimating the cost and profit
Arithmetic calculations
Geometry
Calculus and Statistics
Trigonometry

48. Interior Designing
Interior designing seems to be a fun
and interesting career but, do you
know the exact reality? A lot of
mathematical concepts, calculations,
budgets, estimations, targets, etc.,
are to be followed to excel in this
field. Interior designers plan the
interiors based on area and volume
calculations to calculate and
estimate the proper layout of any
room or building. Such concepts
form an important part of maths.
• Geometry
• Ratios and Percentages
• Mathematical Operations
• Calculus and Statistics

49. ‘Speed, Time, and
Distance’ all these three
things are studied in
mathematical subjects,
which are the basics of
driving irrespective of
any mode of
transportation. Logical reasoning
Numerical Reasoning
Mathematical Operations
Driving

50. • Math is good for the brain
• Math helps you with your
finances
• Math makes you a better cook
• Better problem-solving skills
• Every career uses math
• Great career options
• Math for Fitness
• Helps you understand the
world better
• Time management
• To Save Money
TOP 10 IMPORTANCE OF
MATHEMATICS IN
EVERYDAY LIFE