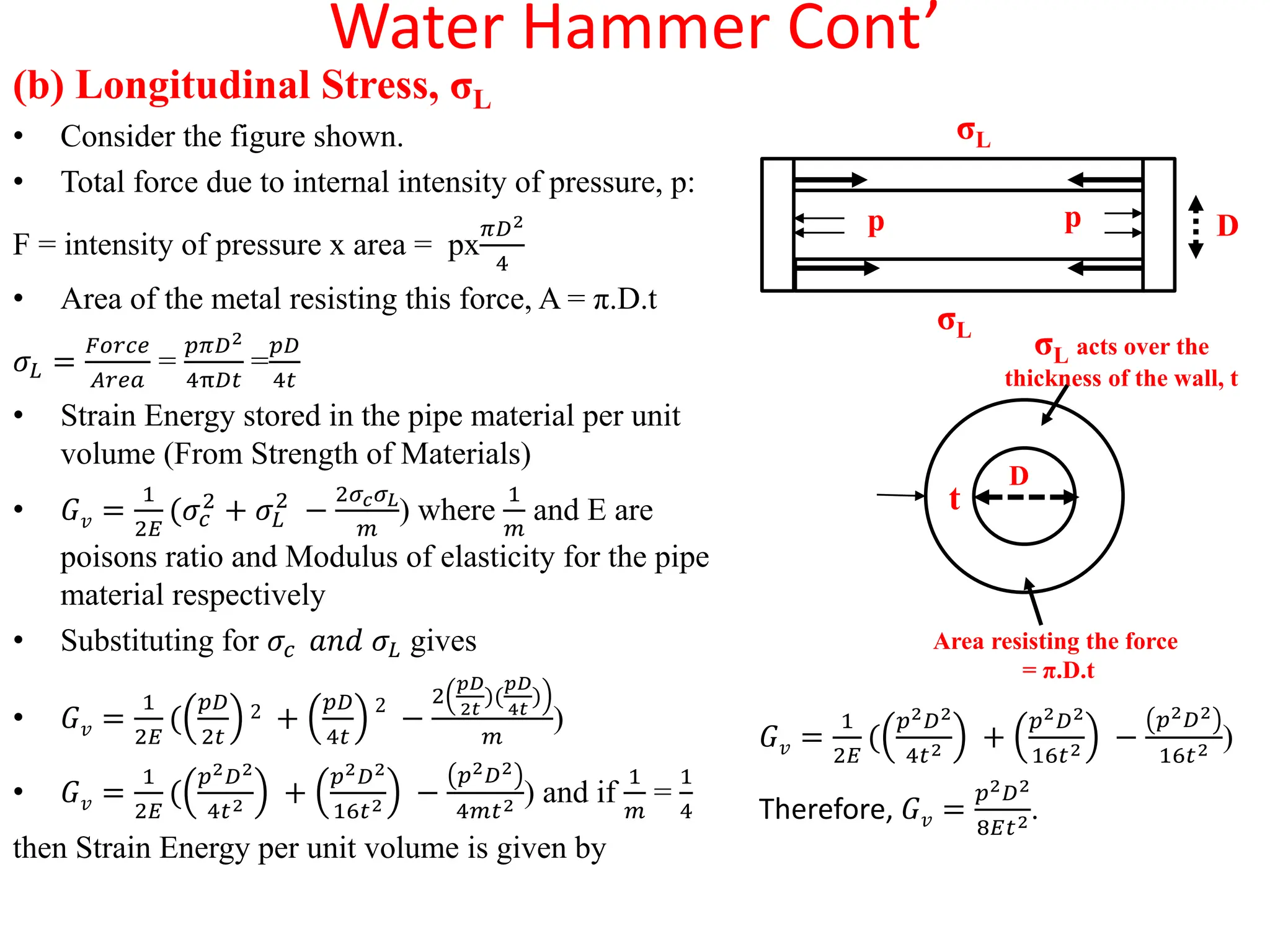
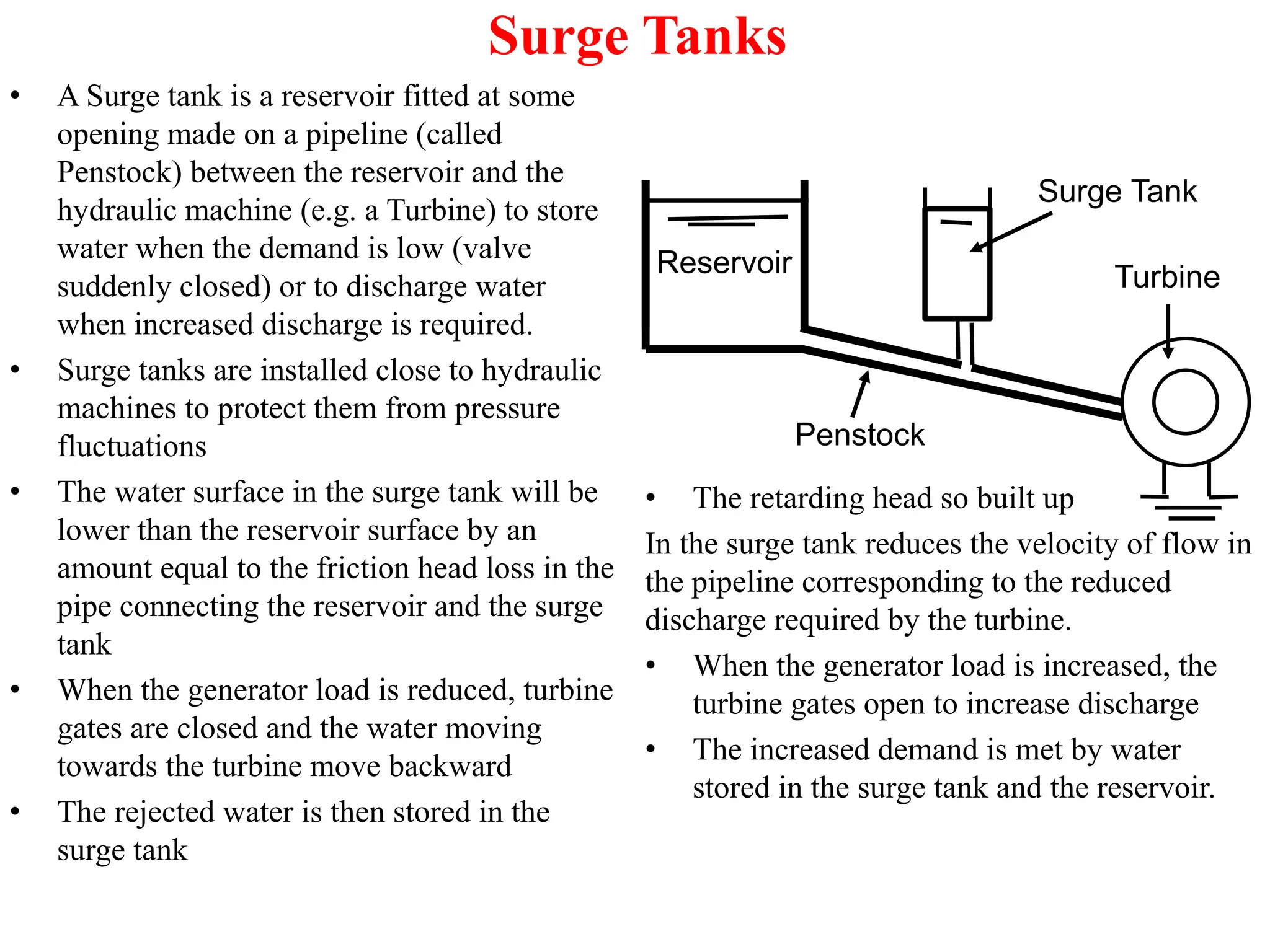
The document discusses the phenomenon of water hammer in pipelines, which occurs when flowing water is suddenly stopped, leading to pressure surges that can cause damage to pipes. It explains the factors influencing pressure rise, the stresses involved, and provides calculations for pressure increases during both gradual and instantaneous valve closures. Additionally, it covers the role of surge tanks in mitigating pressure fluctuations caused by sudden changes in water flow, including examples and derivations related to pipeline pressure and surge tank dynamics.