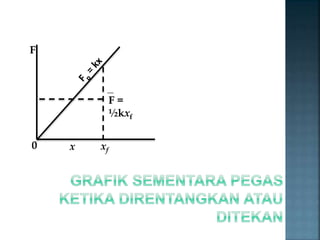
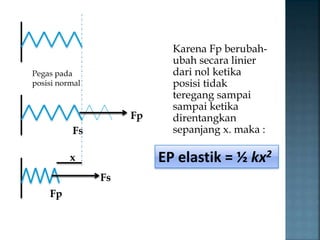
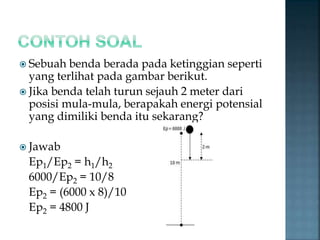
Dokumen tersebut menjelaskan tentang energi potensial, terutama energi potensial gravitasi. Energi potensial adalah energi yang dimiliki sebuah benda karena posisinya, sementara energi potensial gravitasi tergantung pada massa benda, percepatan gravitasi, dan ketinggian benda. Persamaan untuk menghitung energi potensial gravitasi adalah Ep=mgh. Semakin tinggi suatu benda, semakin besar pula energi potensial gravitasinya.

1. Oleh KELOMPOK 4 :
A’yunina Yunitasari
Ayu Faradila
Hkit Fail Nurhasanah

2.  Energi potensial adalah energi yang
memperngaruhi benda karena posisi
(ketinggian) benda tersebut yang mana
kecenderungan tersebut menuju tak terhingga
dengan arah dari gaya yang ditimbulkan dari
energi potensial tersebut.

3. Sebuah benda yang terletak di atas
tanah memiliki energi potensial yang
berhubungan dengan ketinggian dimana
benda itu berada, menurut persamaan:
di mana:
 Ep = energi potensial dalam joule (J)
m = massa benda dalam kg
 g = percepatan gravitasi konstan (9,8 m / s ²)
 h = tinggi di atas tanah atau jarak dari bahwa
benda (m)
C
O
N
T
O
H
Ep = mgh

4. Contoh paling umum dari Energi Potensial adalah
Energi Potensial Gravitasi. Karena setiap bentuk
EP berhubungan dengan satu gaya tertentu
EPgrav = mgy
 Maka makin tinggi suatu benda diatas tanah, makin
besar pula Energi Potensial Gravitasinya
h = EPgrav

5. EPgrav bergantung pada ketinggian vertikal (h)
suatu benda di atas tingkat acuan tertentu dan
tidak tergantung pada lintasan yang diambil.
Misalnya:
Energi potensial gravitasi sebuah buku yang dipegang tinggi
diatas meja, maka EPgrav bergantung pada apakah kita
mengukur y dari permukaan meja, lantai atau dari titik
acuan lainnya.
Maka persamaan ΔEP –lah yang dapat diukur. Untuk
pergerakkan massa m dari titik 1 ke titik 2 = EP benda
antara titik 1 dan titik 2. didapatkan :
WG = -mg (y2-y1)
WG = - ΔEP

6. Contoh lain dari energi potensial adalah
misalnya EP yang dimiliki oleh Pegas.
Persamaan pegas dikenal sebagai
Hukum Hooke
FP = kx
di mana:
 Fp = Gaya Pegas
 k = konstanta pegas
 x = Jarak

7. F
F =
½kxf
0 x xf

8. Karena Fp berubah-ubah
secara linier
dari nol ketika
posisi tidak
teregang sampai
sampai ketika
direntangkan
sepanjang x. maka :
Pegas pada
posisi normal
Fp
Fs
Fs
Fp
x EP elastik = ½ kx2

9.  Sebuah benda berada pada ketinggian seperti
yang terlihat pada gambar berikut.
 Jika benda telah turun sejauh 2 meter dari
posisi mula-mula, berapakah energi potensial
yang dimiliki benda itu sekarang?
 Jawab
Ep1/Ep2 = h1/h2
6000/Ep2 = 10/8
Ep2 = (6000 x 8)/10
Ep2 = 4800 J

10.  ^ William John Macquorn Rankine (1853) "On the general law
of the transformation of energy," Proceedings of the Philosophical
Society of Glasgow, vol. 3, no. 5, pages 276-280; reprinted
in: (1) Philosophical Magazine, series 4, vol. 5, no. 30,pages 106-
117 (February 1853); and (2) W. J. Millar, ed., Miscellaneous
Scientific Papers: by W. J. Macquorn Rankine, ... (London,
England: Charles Griffin and Co., 1881), part II, pages 203-208.
 ^ Smith, Crosbie (1998). The Science of Energy - a Cultural History
of Energy Physics in Victorian Britain. The University of Chicago
Press. ISBN 0-226-76420-6.
 Giancoli,Douglas.2001.Fisika.Jakarta:Erlangga