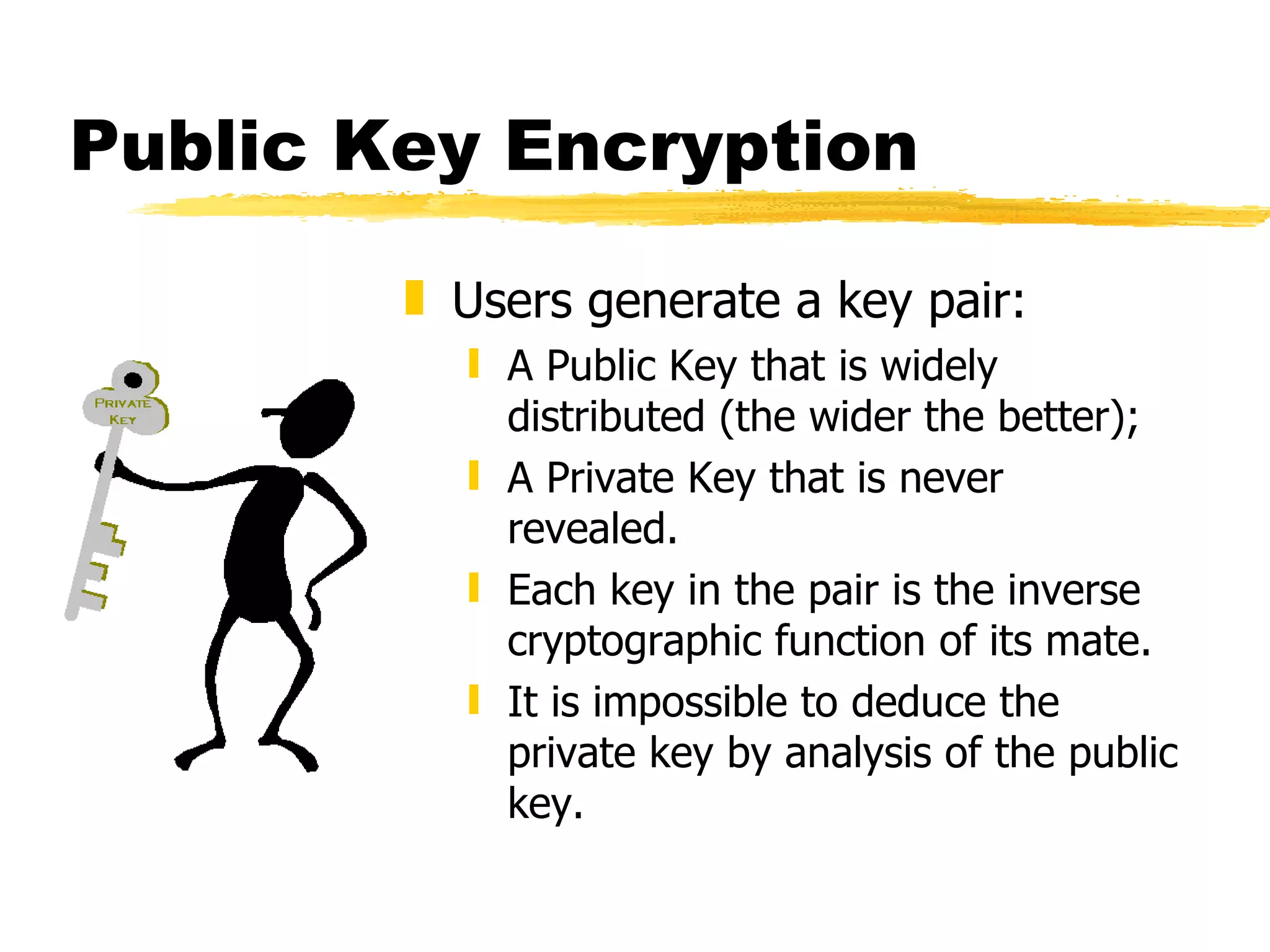
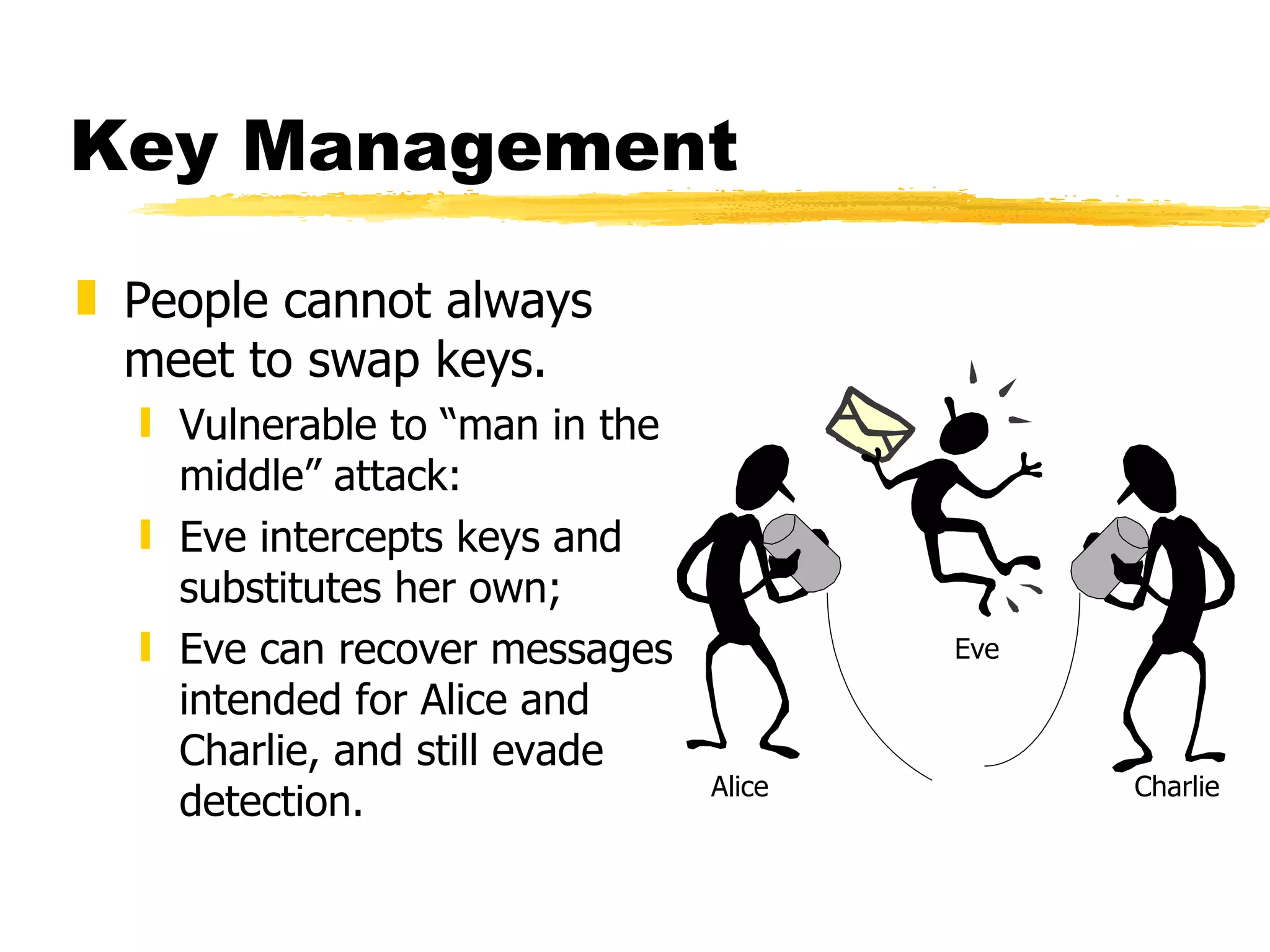
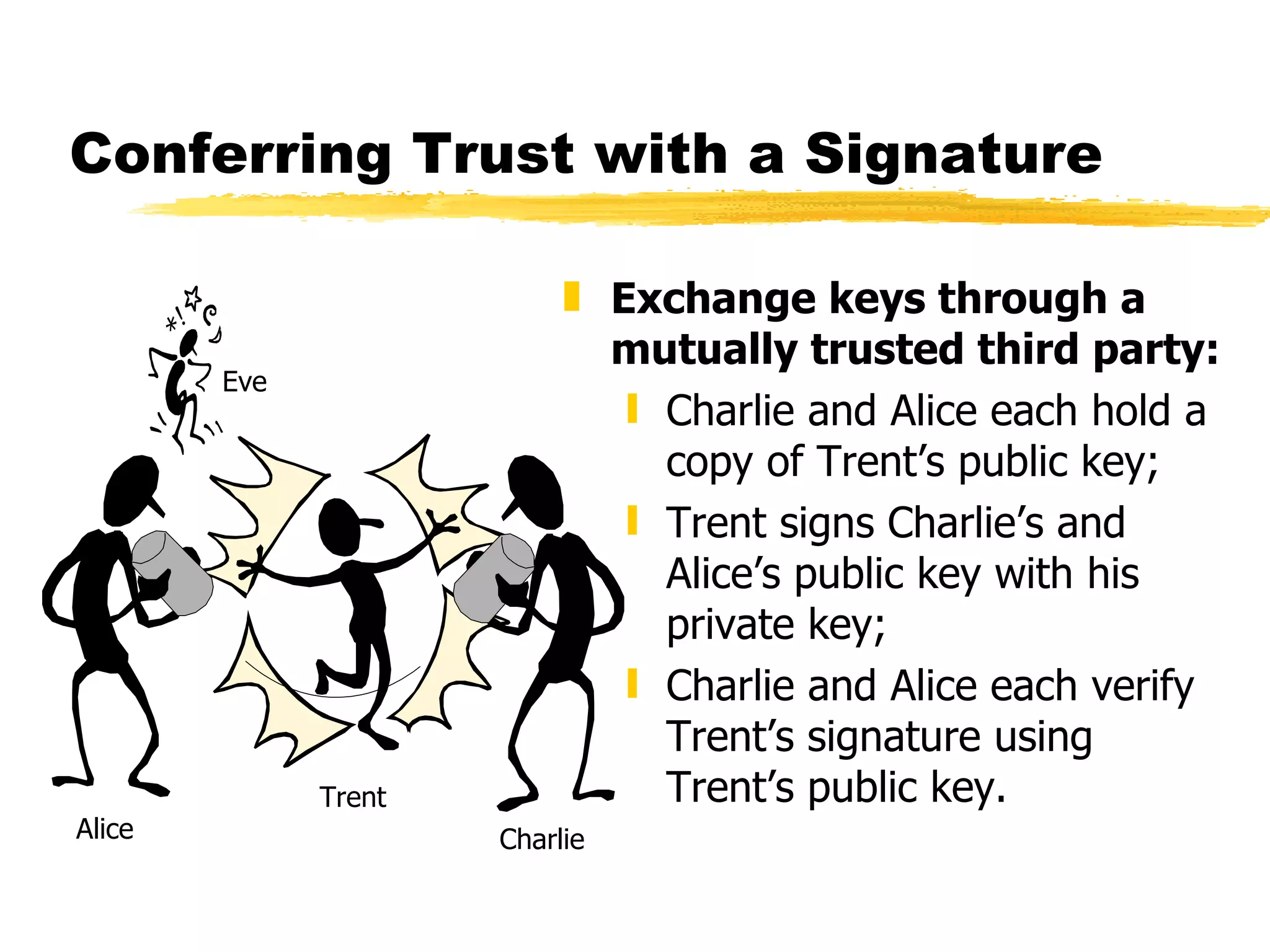
The document discusses the challenges of securing email communications in a distributed corporate network, highlighting vulnerabilities such as data theft and impersonation. It explains the use of public key encryption to ensure secure messaging and authenticate senders, while also addressing key management issues and the risks associated with poor practices. The document concludes by mentioning the evolution of encryption standards and provides a brief overview of the mathematical principles behind key generation and message encryption.

1. E-mail and Encryption Ensuring secure communications in a distributed corporate environment.

2. The Problem The Internet is a distributed network. No one machine controls access to all others. E-mail travels through several servers before arriving at its destination. Every e-mail is stored for a time on every server it passes through. E-mail between the same recipients may never take the same route.

3. Threat Assessment Anyone with access to any of the servers through which our e-mail passes can read it. Anyone with a minimum of technical expertise can forge e-mail to impersonate any sender (or a fictitious sender). We are vulnerable to data theft, data vandals, and electronic imposters.

4. Negating the Threat Public Key (or Asymmetric) Encryption: Permits only the intended recipient to recover the message, no matter who sees the e-mail. Allows positive authentication, so that the recipient can verify the sender’s identity. “ Conferable Trust” extends these benefits to any two parties that need to exchange secure e-mail, even if they have never met .

5. Public Key Encryption Users generate a key pair: A Public Key that is widely distributed (the wider the better); A Private Key that is never revealed. Each key in the pair is the inverse cryptographic function of its mate. It is impossible to deduce the private key by analysis of the public key.

6. Public Key Protocol Alice and Bob meet to exchange public keys. Alice “locks” messages for Bob with her copy of Bob’s public key. Bob uses his private key to “unlock” the message encrypted with his public key. Alice Eve Bob

7. Cryptographic Signatures Messages “locked” with a public key are encrypted to the recipient. Messages “locked” with a private key are digitally signed by the sender. Encrypted messages are recovered with recipient’s private key. Signatures are verified with sender’s public key.

8. Key Management People cannot always meet to swap keys. Vulnerable to “man in the middle” attack: Eve intercepts keys and substitutes her own; Eve can recover messages intended for Alice and Charlie, and still evade detection. Alice Charlie Eve

9. Conferring Trust with a Signature Exchange keys through a mutually trusted third party: Charlie and Alice each hold a copy of Trent’s public key; Trent signs Charlie’s and Alice’s public key with his private key; Charlie and Alice each verify Trent’s signature using Trent’s public key. Alice Charlie Trent Eve

10. Key Distribution Key servers on the Internet are free public key repositories. Users upload their public keys so they can receive secure e-mail from others Users can download keys for sending secure e-mail to the keys’ owners. Users can download keys with which to authenticate signatures.

11. The Good News ... You don’t have to remember much of this. SMSI has selected and will purchase for you software that handles all of these tasks almost automatically. Today, Andrew will hand you a copy of SMSI’s corporate public key, which will act as “Trent” in our example. The software can harvest the keys of SMSI employees and associates off of the key servers. Ensure each key you download is signed by SMSI. Verify the SMSI signature using the key Andrew gives you.

12. The Bad News Encryption systems fail their users because of poor key management. Pick a good pass phrase. Always verify signatures. Encrypt your private key when you’re not using it. Keep a back-up of your keys in a safe place! If possible, try and limit physical access to your computer.

13. Has it ever been cracked? Yes. Two RSA-encrypted messages have been cracked publicly. The first took an estimated 5000 MIPS-years of computing time. The second took about 1300. Both compromised keys were extremely weak, consisting of fewer than 500 bits. Today we use 2,048 bit keys (or stronger), and a more secure algorithm, called Diffie-Hellmann. These efforts each cracked only a single RSA key. Nothing was discovered that could cause any other keys to become less secure.

14. If you really want to know ... Find two very large primes, p and q. Find n=pq (the public modulus). Choose e, such that e < n and relatively prime to (p-1)(q-1). Compute d such that ed=1[mod (p-1)(q-1)]. e is the public exponent and d is the private one. The public key is (n,e), and the private key is (n,d). To encrypt, divide the target message into blocks smaller than n and perform modular exponentiation: c=m^e mod n Decryption is the inverse operation: m=c^d mod n … et Voila!