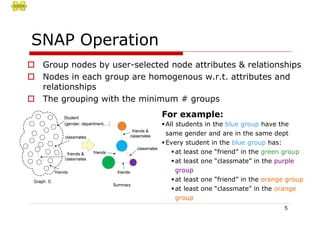
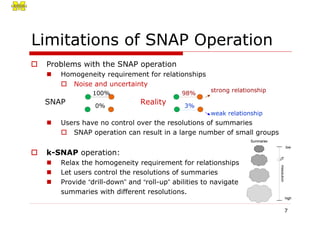
The document proposes two novel graph aggregation operations, SNAP and k-SNAP, to efficiently summarize large graphs. SNAP groups nodes that are homogeneous in attributes and relationships, while k-SNAP allows users to specify the number of groups k and relaxes relationship homogeneity. Experimental results on real and synthetic graphs demonstrate that k-SNAP produces meaningful multi-resolution summaries and the top-down evaluation approach is more efficient than the bottom-up approach, especially for smaller k values.

1. Yuanyuan Tian (University of Michigan)
Richard A. Hankins (Nokia Research Center)
Jignesh M. Patel (University of Michigan)
Efficient Aggregation for
Graph Summarization

2. Motivation
Graphs are everywhere
Social networks, biological networks
Graph datasets growing rapidly in size.
Impossible to understand by mere visual
inspection.
Need: Graph Summarization
DB Coauthorship
7,445 nodes, 19,971 edges
Number of Facebook Users
0
10,000,000
20,000,000
30,000,000
40,000,000
50,000,000
Jun-04
Sep-04
Dec-04
Mar-05
Jun-05
Sep-05
Dec-05
Mar-06
Jun-06
Sep-06
Dec-06
Mar-07
Jun-07
Sep-07
Dec-07

3. 33
Existing Methods
Statistical methods
Limited information, hard to interpret & manipulate.
Frequent subgraph mining methods
Produce a large number of results.
Graph partitioning methods
Largely ignore node attributes.
Graph compression
Compact storage.
Graph visualization
Ben’s keynote talk.
MDL-based graph summarization (Nisheeth’s talk)

4. 44
Solution: Graph Aggregation
Two well-defined novel graph aggregation operations:
SNAP & k-SNAP
Summarization based on user-selected node
attributes and relationships.
Produce summaries with controllable resolutions.
Provide “drill-down” and “roll-up” abilities to navigate
multi-resolution summaries.
Efficient algorithms
Produce meaningful summaries for real applications.
Efficient and scalable for very large graphs.

5. 55
SNAP Operation
Group nodes by user-selected node attributes & relationships
Nodes in each group are homogenous w.r.t. attributes and
relationships
The grouping with the minimum # groups
For example:
All students in the blue group have the
same gender and are in the same dept
Every student in the blue group has:
at least one “friend” in the green group
at least one “classmate” in the purple
group
at least one “friend” in the orange group
at least one “classmate” in the orange
group
friends

6. 66
Evaluating SNAP Operation
Top-Down Approach
Step 1: group nodes just based on user-selected attributes.
Iterative Step:
while a group breaks homogeneity requirement for relationships
split the group based on its relationships with other groups
SplitGroup
C
A
B
A
A
A
B
B
A
C
A
A
C
A

7. 77
Limitations of SNAP Operation
Problems with the SNAP operation
Homogeneity requirement for relationships
Noise and uncertainty
Users have no control over the resolutions of summaries
SNAP operation can result in a large number of small groups
k-SNAP operation:
Relax the homogeneity requirement for relationships
Let users control the resolutions of summaries
Provide “drill-down” and “roll-up” abilities to navigate
summaries with different resolutions.
SNAP Reality
100%
0%
98%
3%
strong relationship
weak relationship

8. 8
k-SNAP Operation
Users control # groups in the resulting summary: k
Maintain homogeneity requirement for attributes.
Relax homogeneity requirement for relationships.
Assess the quality of a summary
ΔMeasure
Δ=∑{δgi,gj
(gi) + δgi,gj
(gj) }
gi,gj
δgi,gj
(gi)=
|Pgi,gj
(gi)| if pi,j≤0.5
|gi|−|Pgi,gj
(gi)| otherwise
40
100
80
20
40
100
80
20
(95,19):95%
Δ= 0
5% ≤ 50% (weak)
Δ+= 3+4 extra participants
95% > 50% (strong)
Δ+= (100-95)+(20-19) missing participants
……

9. 99
Evaluating k-SNAP Operation
Goal: Find the summary of size k with the
minimum Δ value (best quality)
Proved to be NP-Complete!
Infeasible to produce exact k-SNAP summaries.
Alternative: heuristics
Top-Down Approach
Bottom-Up Approach

10. 1010
Top-Down Approach
Similar to the SNAP evaluation algorithm (coarse fine)
(Difference) At each iteration, it needs to decide:
which group to split?
how to split the group?
Heuristics:
Split a group into two subgroups at each iteration
Find gi with the maximumδgi,gj
(gi) (the most contribution to Δ)
Split group gi based on whether the nodes in gi connect to gj.
gi gj
gj
gi’’
gi’
max
Δ=∑{δgi,gj
(gi) + δgi,gj
(gj) }
gi,gj
Split

11. 1111
Bottom-Up Approach
Compute the SNAP summary first (fine coarse)
Iteratively merge two groups until the # groups is k
Which two groups to merge?
Heuristics:
Same attribute values
Similar neighbors
Similar participation ratio
Merge two groups with the minimum MergeDist.
MergeDist(gi, gj)=∑| pi,k - pk,j |
k≠i,j
gi
gj
gk
pk,j
pi,k

12. 1212
Experimental Evaluation
Implementation
C++ on top of PostgreSQL
Evaluation Platform
2.8GHz P4, 2GB RAM, 250GB SATA disk, FC2
PostgreSQL: version 8.1.3, 512 MB buffer pool
Evaluation Measures:
Effectiveness & Efficiency
Verified by the SIGMOD repeatability committee.

13. 1313
Effectiveness: DB Coauthorship
DBLP Database Coauthorship Graph
(7,445 nodes, 19,971 edges)
Node Attributes:
name (string), numPub (int), prolific (LP, P, HP)
LP:[1, 5], P:[6, 20], HP:[21, -]
Relationship: coauthorship
SNAP
Attribute: prolific
Relationship: coauthorship
3,569 groups,
11,293 group relationships

14. 1414
Effectiveness: DB Coauthorship
K=4
K=5K=6K=7
SNAP
Attribute: prolific
k-SNAP
Attribute: prolific
Relationship: coauthorship
36
1.66
1.23
2.23
1.26
1.55
9.74

15. Effectiveness: DB Coauthorship
Impact of Double-Blind
Reviewing on SIGMOD
0
0.1
0.2
0.3
0.4
Average#Publications
VLDB 0.161 0.305
SIGMOD 0.125 0.217
1994-2000 2001-2007
89%
73%
0
0.1
1994-2000 2001-2007
0
0.1
1994-2000 2001-2007
-12%
107%
26%
139%
0
1
2
3
4
5
1994-2000 2001-2007
0
1
2
1994-2000 2001-2007
0
0.1
0.2
1994-2000 2001-2007
0
0.1
0.2
0.3
0.4
1994-2000 2001-2007
0
0.1
0.2
0.3
1994-2000 2001-2007
91%
75%
50%
26%
73%
32%
165%
101%
99%
161%

16. 1616
k-SNAP: Top-Down vs. Bottom-Up
Quality
Measure: Δ/k
Top-down beats
bottom-up for
small k values
Execution Time
Top-down is
much faster than
bottom-up
0
500
1000
1500
8
16
32
64
128
256
512
1024
2048
3569
k (log scale)
Delta/k
Top-Down
Bottom-Up
1
10
100
1000
10000
100000
1 10 100 1000 10000
k(log scale)
ExecutionTime
(logscale)
Top-Down
Bottom-Up
Overall, top-down is the winner!
Dataset: DBLP DB Coauthorship Graph

17. 1717
Efficiency: Synthetic Graphs
0
1000
2000
3000
4000
5000
6000
7000
8000
9000
0 200,000 400,000 600,000 800,000 1,000,000
Graph Size (#nodes)
ExecutionTime(sec)
k=10
k=100
k=1000
Dataset: Synthetic Power-Law Graphs (by GTgraph)
(avg degree:5)

18. Conclusion
Database-style aggregation for graph summarization
Customized summaries
Controllable resolutions
“drill-down” and “roll-up” abilities
Meaningful summaries for real applications
Efficient and scalable for very large graphs
Incorporated in Periscope/GQ graph querying system
Combined with other graph operations to perform complex
analysis on graphs (VLDB’08 Demo)

19. 1919
Questions?
Suggestions?
Thanks! ☺☺☺☺