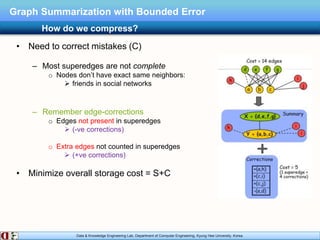
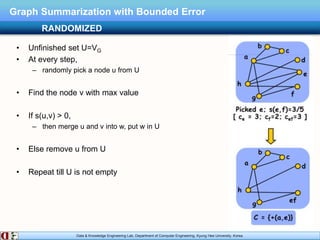
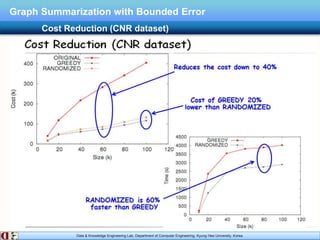
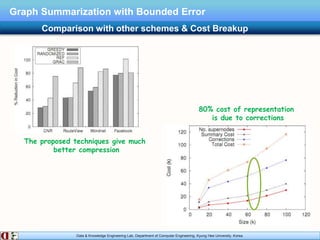
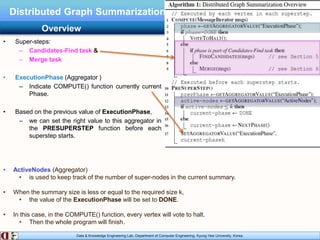
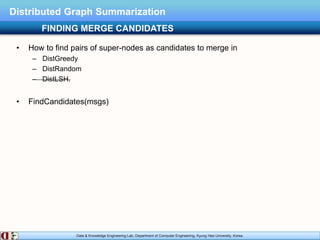
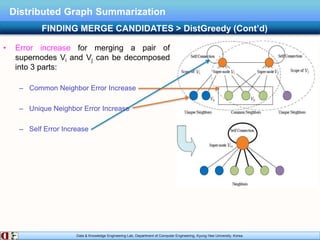
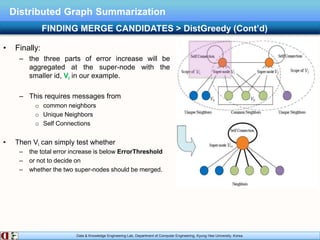
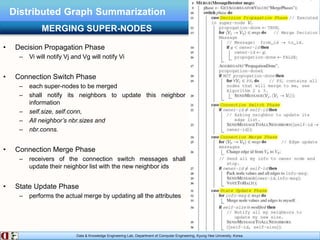
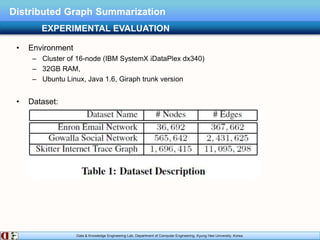
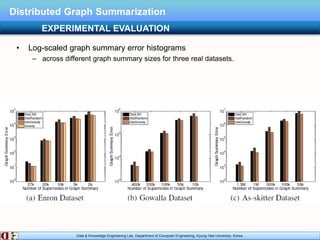
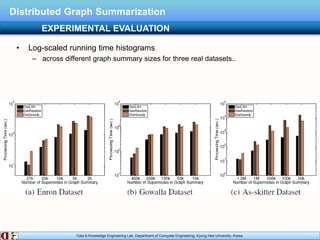
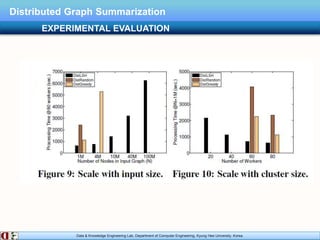
The document describes research on distributed graph summarization algorithms. It introduces three distributed graph summarization algorithms (DistGreedy, DistRandom, DistLSH) that can scale to large graphs by distributing computation across machines. The algorithms share a common framework of iteratively merging super-nodes representing aggregated subsets of nodes, but differ in how they select candidate pairs of super-nodes to merge. Experimental evaluation on real-world graphs demonstrates the ability of the proposed distributed algorithms to summarize large graphs in a parallelized manner.