This document contains a summary of 9 multi-part mathematics problems involving concepts like algebra, geometry, trigonometry, matrices and percentages. For brevity, the summary focuses on stating the key steps and conclusions of each problem rather than including all working details.

1. DHS 2009 Sec 4 SAP Preliminary Exam Mathematics Paper 2
p2 − q p
1 (a) Given that = , express q in terms of p. [3]
q 2
(b) Express as a fraction in its lowest terms,
3 − 2x x
− . [3]
x − 5x + 6 3 − x
2
Answer:
p2 − q p2
1 (a) =
q 4
q 4
=
p 2
4 + p2
4 p2
q=
4 + p2
(b)
3 − 2x
−
x
=
(3 − 2x ) + x ( x − 2)
x − 5x + 6 3 − x
2
( x − 2 )( x − 3)
=
( x − 1)( x − 3)
( x − 2 )( x − 3)
x −1
=
x−2
2
1st 2nd 3rd
pattern pattern pattern
In the diagram above, each pattern is made up of dots, lines and small triangles. In the
1st pattern, there are 9 dots, 15 lines and 7 small triangles.

2. (a) How many small triangles are there in the
(i) 4th pattern,
(ii) n th pattern? [2]
(b) How many lines are there in the n th pattern? [1]
(c) If there are d dots, l lines and T triangles in one of these patterns, write down
an equation connecting d, l and T. [2]
2 (a) (i) 16
(ii) 3n + 4
(b) 6n + 9
(c) ( 6n + 9 ) − ( 3n + 6 ) + 1 = ( 3n + 4 )
l − d +1 = T
3 A cylindrical container which has an internal diameter of 60 cm and an internal height
of 1.05 m weighs 7 kg when empty.
(a) Find the weight of the container when it is full of oil, if the density of oil is
7
g/cm3 .
9
(b) How many times will the oil in the container fill a hemispherical bowl of
22
internal diameter of 7 cm? [Take π = ] [5]
7
(c) Find the internal surface area of the hemispherical bowl in contact with the
oil. [2]
3 (a) Volume of the cylindrical container
22
= × 302 ×105
7
= 297 000 cm3
Weight of the cylindrical container
7
= 7 + × 297
9
= 7 + 231 = 238 kg

3. 3
(b) Volume of a hemispherical bowl
1 4 22
= × × × 3.53
2 3 7
539
= cm3
6
Number of times the oil will fill the bowl
539
= 297 000 ÷
6
6
= 3306
49
(c) Internal surface area in contact with oil
1 22
= × 4 × × 3.52
2 7
= 77 cm 2
4 In May 2007, the Credit Bureau Singapore released the following data on
Singaporeans’ home loans/ mortgages for the period from March 2005 to March
2007.
No of Singaporeans with: March 2005 March 2006 March 2007
2 or more home loans 19901 25977 41078
2 or more home loans valued at 1416 1962 2925
a total of more than S$1 million
More than S$1 million 2381 2381 4291
in home loans
The information for those Singaporeans with 2 or more home loans over this period of
⎛ 19901 ⎞
comparison can be represented by the matrix P = ⎜ 25977 ⎟ .
⎜ ⎟
⎜ 41078 ⎟
⎝ ⎠
The information for those Singaporeans with 2 or more home loans valued at a total
of more than S$1 million over this period of comparison is represented by a matrix Q.
(i) Write down the matrix Q. [1]
(ii) Calculate the matrix ( P − Q ) . [1]
[Turn over

4. (iii) Describe what is represented by the elements of ( P − Q ) . [1]
The information for those Singaporeans with home loans in 2005 is represented by the
matrix A = (19901 1416 2381) .
Information for those Singaporeans with home loans in 2007 is represented by the
matrix B.
(iv) Write down the matrix B. [1]
(v) Show that the matrix C, in terms of A and/ or B, which has its elements
showing the increase of each category over the period of 2005 to 2007 is
( 21177 1509 1910 ) . [1]
⎛ 1 ⎞
⎜ 19901 0 0 ⎟
⎜ ⎟
1
(vi) A matrix D is given by ⎜ 0 0 ⎟ . Evaluate (100 CD ) , rounding
⎜ 1416 ⎟
⎜ ⎟
⎜ 0 1 ⎟
⎜ 0 ⎟
⎝ 2381 ⎠
off each element to the nearest whole number. [1]
(vii) Describe what is represented by the elements of the matrix (100 CD ) . [2]
⎛ 1416 ⎞
4 (i) Q = ⎜ 1962 ⎟
⎜ ⎟
⎜ 2925 ⎟
⎝ ⎠
⎛ 19901 − 1416 ⎞
(ii) ( P − Q ) = ⎜ 25977 − 1962 ⎟
⎜ ⎟
⎜ 41078 − 2925 ⎟
⎝ ⎠
⎛ 18485 ⎞
= ⎜ 24015 ⎟
⎜ ⎟
⎜ 38153 ⎟
⎝ ⎠
(iii) The elements of (P − Q) represent the information for those
Singaporeans with 2 or more home loans valued at a total of less than or equal
to S$1 million over this period of comparison.
(iv) B = ( 41078 2925 4291)
(v) C = ( 41078 − 19901 2925 − 1416 4291 − 2381)
= ( 21177 1509 1910 ) [shown]

5. 5
⎛ 1 ⎞
⎜ 19901 0 0 ⎟
⎜ ⎟
1
(vi) (100 CD ) = 100 ( 21177 1509 1910 ) ⎜ 0
⎜
0 ⎟
⎟
1416
⎜ ⎟
⎜ 0 1 ⎟
⎜ 0 ⎟
⎝ 2381 ⎠
= (106 106 80 )
(vii) 106 represents the percentage increase in number of Singaporeans
having 2 or more home loans over the period of March 2005 to March 2007.
106 represents the percentage increase in number of Singaporeans having 2 or
more home loans valued at more than S$1 million over the period of March
2005 to March 2007.
80 represents the percentage increase in number of Singaporeans with home
loans of more than S$1 million over the period of March 2005 to March 2007.
5 In Singapore, the rate for the usage of water for the month of July in 2009 is as
follows:
Water used : $1.17 per m3
Water borne fee : $0.28 per m3
Sanitary Appliance fee : $2.80 per fitting
Water Conservation tax : 30% of the amount payable for water used
Goods and Services tax (GST): 7% of all the above fees/ tax
(i) In July, the GST payable for water used only by a Pasir Ris 5-room household
is $3.11.
Calculate the amount, excluding GST, paid for water used in July by this
household. [2]
(ii) Show that the amount of water used by this household in July, is
approximately 38.0 m3. [1]
(iii) Hence, find the overall water bill if this household has 2 sanitary fittings. [2]
(iv) If the national average of water usage per month for a typical 5-room HDB flat
in Singapore is 19.1 m3,
(a) how many percent above average is the water usage for this
household? [2]
[Turn over

6. (b) what is the average water usage per day for a typical 5-room HDB flat
in Singapore for the month of July? [1]
5 $3.11×100
(i) Amount paid for water used only =
7
= $44.43 (to nearest cent)
44.43
(ii) = 37.97 ≈ 38.0 m3 (to 3 sig. fig.)
1.17
(iii) ( 38.0 ×1.17 ×1.3 + 38.0 × 0.28 + 2 × 2.80 ) ×1.07
= $79.17 (to nearest cent)
38.0 − 19.1
(iv) (a) ×100 = 49.7% (to 3 sig. fig.)
38.0
19.1
(b) = 0.616 m3 (to 3 sig. fig.)
31
6
C
P
D
B
42°
R A
H
The points D, H, R and P lie on the circumference of a circle. DR is a diameter of the
ˆ
circle, DA is a tangent to the circle at D, CBH is a straight line and DRH = 42° .
(a) Find, with reason,

7. 7
(i) ˆ
DHR , (ii) ˆ
RDH ,
(iii) ˆ
DAR , (iv) ˆ
RPH . [4]
(b) ˆ
Given also that DBH = 107° , find
(i) ˆ
RCH , (ii) ˆ
DHC . [2]
(c) Show that the triangles DHR and AHD are similar. [2]
(a) (i) ˆ
DHR = 90 ( in a semicircle)
6
ˆ
RDH = 90 − 42 (complementary s, ΔDHR)
(ii)
= 48
ˆ
RDA = 90 (tangent ⊥ radius)
(iii) ˆ
DAR = 90 − 42 (complementary s, ΔRDA)
= 48
ˆ ˆ
RPH = RDH ( s in the same segment)
(iv)
= 48
ˆ ˆ ˆ
RCH + CDB = DBH (ext. = sum of int. opp. s)
(b) (i) ˆ
RCH = 107 − 90
= 17
ˆ ˆ ˆ
DHC + RCH = RDH (ext. = sum of int. opp. s)
(ii) ˆ
DHC = 48 − 17
= 31
ˆ ˆ
DHR = 90 = AHD ( s on a straight line)
ˆ ˆ
RDH = 48 = DAH ((a)(ii)&(iii))
(c) ˆ ˆ
DRH = ADH (3rd s of Δs)
Since there are 3 pairs of equal corresponding s,
triangles DHR and AHD are similar. (Shown)
Q
7
P
R S
A B C
[Turn over

8. The diagram shows three semicircles each of radius 18 cm with centres at A, B and C
in a straight lines shown above. A fourth circle centre at P and with radius r cm is
drawn to touch the other three semicircles. Given that BPQ is a straight line which is
tangential to the two semicircles with centres A and C at point B,
(a) show that r = 4.5 cm, [3]
(b) ˆ
Find the value of PAC in radians, [2]
(c) Calculate the area of the shaded region. [3]
(18 + r ) = (18 − r ) + 182
2 2
ΔABP :
7
(a) 182 + 2 (18 ) r + r 2 = 182 − 2 (18 ) r + r 2 + 182
r = 4.5
ˆ 13.5
tan PAC =
(b) 18
ˆ
PAC = 0.644 rad
(c) Area of shaded region
⎡1 1 1 ⎛π ⎞⎤
2 ⎢ ×18 ×13.5 − ×182 × ( 0.644 ) − × 4.52 × ⎜ − 0.644 ⎟ ⎥
= ⎣2 2 2 ⎝2 ⎠⎦
= 15.7 cm2

9. 9
8
P Q
0.874 km
1.3 km
R
North
T
26.3°
S
In the diagram, ST represents the northward-bound MRT line. The quadrilateral PQRS
formed the fence that boarded a carnival for the F1 Night Race in September. The
point P is due west of S and PS is parallel to QR. Given that PRT is a straight line,
ˆ ˆ
QR = 0.874 km, PS = 1.3 km, RST = 26.3 and SRT = 90 . Find
(i) the bearing of R from T, [1]
(ii) the length of PR, [1]
Hence, show that PQ = 0.54 km, [2]
(iii) ˆ
QPR . [1]
(iv) The Singapore Flyer is built at the point Q. If the angle of depression of P
from the highest point of the wheel is 8° , find the height, in metres, of the
entire flyer. [1]
(v) A man walked from P along PS and reached a point X such that the angle of
elevation of the highest point of the wheel is a maximum. Find the angle of
elevation, (you may ignore the height of the man). [3]
ˆ
RTS = 90 − 26.3
8 (i)
= 63.7 (complementary angles)
Hence, the bearing of R from T is 180 + 63.7 = 243.7
(ii) ˆ
ΔPST : SPT = 26.3
PR
cos 26.3 =
1.3
PR = 1.17 km (3 sig. fig.)
[Turn over

10. PQ 2 = PR 2 + ( 0.874 ) − 2 ( PR )( 0.874 ) cos 26.3
2
PQ = 0.54 km (Shown)
ˆ
sin QPR sin 26.3
(iii) =
0.874 PQ
ˆ
QPR = 45.4 (to 1 dec. pl.)
h
(iv) tan 8 =
PQ
Height of the entire flyer is 76.4 m (to 3 sig. fig.)
XQ = PQ sin ( 45.4 + 26.3)
(v)
= 0.5164 (to 4 sig. fig.)
Let the angle of elevation be θ
h
tan θ =
XQ
θ = 8.4 (to 1 dec. pl.)

11. 11
9 According to the Straits Times, a check on a random selection of basic goods at
several supermarkets in Singapore revealed an increase in the prices since the
beginning of the year. In particular, a pack of fresh chicken (between 1 to 1.3 kg) now
cost 70 cents more than its original cost at the beginning of the year.
In 2008, Yusof budgeted $234 for fresh chicken to be used during his wedding
reception in January 2009.
(i) If x represents the number of packs of fresh chicken (between 1 to 1.3 kg)
which Yusof could buy at the beginning of 2009, write down an expression, in
terms of x, for the original cost of a pack of fresh chicken (between 1 to 1.3
kg). [1]
(ii) Yusof found that he would get 7 packs of fresh chicken (between 1 to 1.3 kg)
less than that at the beginning of the year if he decided to delay the wedding
reception till September 2009.
Write down an expression, in terms of x, for the current cost of a pack of fresh
chicken (between 1 to 1.3 kg). [1]
(iii) Write down an equation in x, and show that it reduces to x 2 − 7 x − 2340 = 0 . [3]
(iv) Solve the equation x 2 − 7 x − 2340 = 0 . [2]
(v) Calculate the percentage increase in the price of a pack of fresh chicken
(between 1 to 1.3 kg). [2]
234
9 (i) The original cost of a pack of fresh chicken (between 1 to 1.3 kg) = $
x
234 234 7
(iii) − =
x−7 x 10
234 x − 234( x − 7) 7
=
x( x − 7) 10
10 [ 234 x − 234 x + 1638] = 7 x 2 − 49 x
7 x 2 − 49 x − 16380 = 0
⇒ x 2 − 7 x − 2340 = 0 [shown]
(iv) x 2 − 7 x − 2340 = 0
( x − 52 )( x + 45) = 0
x = 52 or x = −45 (rejected)
(v) GKC could buy 52 – 7 = 45 packs now.
[Turn over

12. 234
(vi) original price = $ = $4.50
52
0.70
Percentage increase in price per pack = × 100%
4.50
5
= 15 %
9
10 In a recent Olympic diving event, a male participant stood on a platform and
performed a dive into the water.
During the dive, the horizontal distance of the participant away from the platform,
x m, and the corresponding vertical distance of the participant above the platform,
y m, are related by the equation
13 x2
y= x− .
10 2
Some corresponding values of x and y are given in the table below.
x 0 1 2 3 4 5 6
y 0 0.8 0.6 −0.6 −2.8 −6 p
(a) Find the value of p. [1]
(b) Using a scale of 2 cm to 1 unit, draw a horizontal x-axis for 0 ≤ x ≤ 6 .
Using a scale of 2 cm to 1 unit, draw a vertical y-axis for − 11 ≤ y ≤ 1 .
On your axes, plot the points given in the table and join them with a smooth
curve. [3]
(c) Use your graph to find the distance(s) the participant was from the platform the
when he was 0.5 m above the platform. [2]
(d) Use your graph to find the maximum height above the platform reached by the
participant. [1]
(e) By drawing a tangent, find the gradient of the curve at the point (3, −0.6).
What can be said about the movement of the participant at this instant? [3]
(f) The participant entered the water when he was 4.4 m away from the platform
horizontally. Use your graph to determine the height of the platform above the
water. [1]

13. 13
(g) Is the graph useful in finding the position of the participant beyond a
horizontal distance of 4.4 m? Justify your answer. [1]
(a) p = −10.2
10
(b)
(b) Correct axes --- B1
Points plotted correctly --- B1
Shape --- B1
[Turn over

14. (c) x = 0.45 or 2.15
(d) Maximum height = 0.85 m
(e) Drawing of correct tangent line
Gradient = −1.7
The participant is moving downwards and
away from the platform at this point.
(f) Distance the platform is above the water = 4 m
(g) No, because beyond 4.4 m, the participant has entered the water, and after
entering the water, the water will slow down his movement.

15. 15
11 A bag holds some coloured balls. There are 15 red, 3 blue and 2 white balls. Two
balls are picked from the bag at random, without replacement. The tree diagram
below shows the possible outcomes and some of their probabilities.
Second Pick
b Red
First Pick 3
Red 19 Blue
3
4 2
White
19
15
19 Red
3 2
20 19
Blue Blue
c
White
15
a Red
19
White d Blue
1
White
19
(a) State the values of a, b, c and d. [2]
(b) Expressing your answers as a fraction in its lowest terms, find the probability
that
(i) both balls are white, [1]
(ii) at least one ball is red. [2]
1 14 2 3
11 (a) a= , b= , c= and d =
10 19 19 19
1 1
(b) (i) P (both white) = ×
10 19
[Turn over

16. 1
= .
190
(ii) P (at least 1 ball is red) =
⎛ 3 14 ⎞ ⎛ 3 3 ⎞ ⎛ 3 2 ⎞ 18
⎜ × ⎟ + 2⎜ × ⎟ + 2⎜ × ⎟ =
⎝ 4 19 ⎠ ⎝ 4 19 ⎠ ⎝ 4 19 ⎠ 19
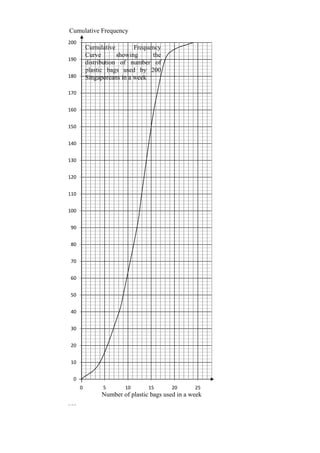
12 In a bid to make our society more environmentally friendly, a survey was conducted
and the cumulative frequency curve shown illustrates the number of plastic bags used,
by 200 Singaporeans in a week.
(a) Use the graph to find
(i) the median number of plastic bags used, [1]
(ii) the lower quartile, [1]
(iii) the interquartile range, [1]
(b) A person is considered to be a ‘reddie’ if he uses more than 18 plastic bags in
a week. A Singaporean is chosen at random. Calculate, leaving your answer
as a fraction in its lowest term, the probability of getting a ‘reddie’. [2]
(c) Given that 19.5% of Singaporean surveyed are ‘green crusaders’, use the
graph to find the minimum number of plastic bags used by a Singaporean who
is not a green crusader. [2]
(d) The frequency table for this set of data is given below. Showing your method
clearly, prove that the values are as shown in the table. [2]
Number of plastic Number of Singaporeans
bags used per week surveyed
0< x≤4 10
4< x≤8 29
8 < x ≤ 12 52
12 < x ≤ 16 75
16 < x ≤ 20 30
20 < x ≤ 24 4
(e) Calculate,
(i) the mean, [3]
(ii) the standard deviation. [2]

17. 17
(f) A similar survey was also conducted in Hong Kong and the table below shows
the results of the processed data.
Mean 11.96 Compare, briefly, the results for the
Standard Deviation 2.90 two countries. [1]
[Turn over

18. Cumulative Frequency
200
Cumulative Frequency
Curve showing the
190
distribution of number of
plastic bags used by 200
180 Singaporeans in a week
170
160
150
140
130
120
110
100
90
80
70
60
50
40
30
20
10
0
0 5 10 15 20 25
Number of plastic bags used in a week
200

19. 19
(ai) Median = 12.5 plastic bags
1 (aii) Lower Quartile = 9 plastic bags
2 (aiii) Upper Quartile = 15 plastic bags
Interquartile range = 15 – 9 = 6 plastic bags
(b) 200 – 190 = 10 ‘reddies’ who used more than 18 plastic bags in a week.
10 1
Probability of getting a reddie = =
200 20
19.5
(c) From the graph, there are × 200 = 39 green crusaders who used 8
100
or less plastic bags in a week.
So, the minimum number of plastic bags used by a non-green crusader in a
week = 8 + 1
= 9
(d)
Number of plastic bags Number of Singaporeans Mid-
used per week surveyed, f values, x’
0< x≤4 10 – 0 = 10 2
4< x≤8 39 – 10 = 29 6
8 < x ≤ 12 91 – 39 = 52 10
12 < x ≤ 16 166 – 91 = 75 14
16 < x ≤ 20 196 – 166 = 30 18
20 < x ≤ 24 200 – 196 = 4 22
(ei) Mean =
∑ fx ' = 2392
∑f 200
= 11.96 plastic bags
∑ fx ' ⎛ ∑ fx ' ⎞
2
2
−⎜
⎜ ∑f ⎟
(eii) Standard Deviation =
∑f ⎝
⎟
⎠
2
32640 ⎛ 2392 ⎞
= −⎜ ⎟
200 ⎝ 200 ⎠
= 4.49 plastic bags (to 3 s.f.)
(f) Hong Kong has a smaller spread of number of plastic bags used.
[Turn over