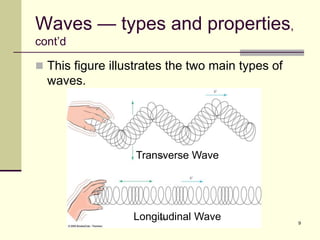
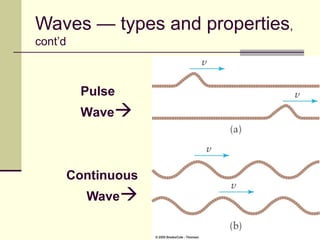
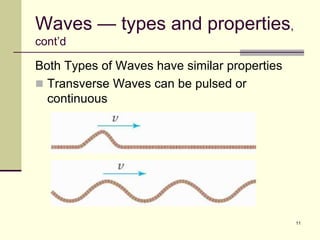
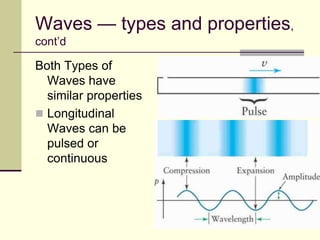
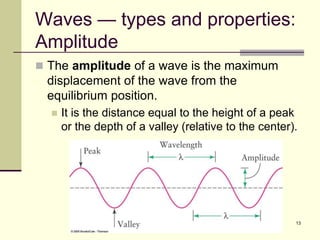
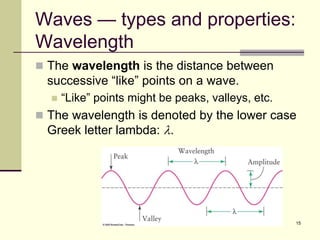
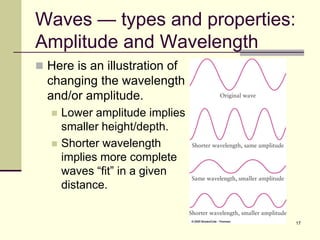
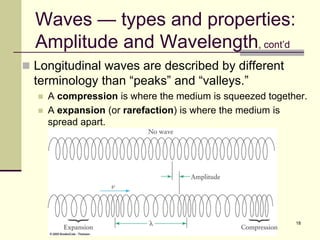
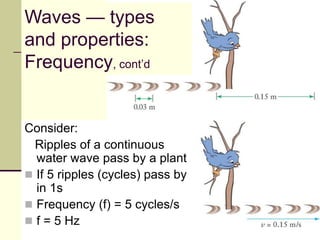
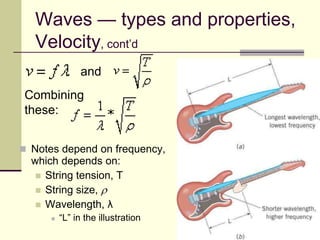
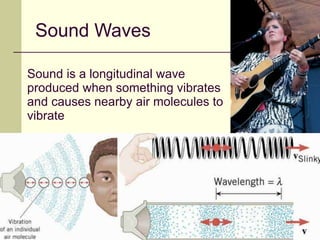
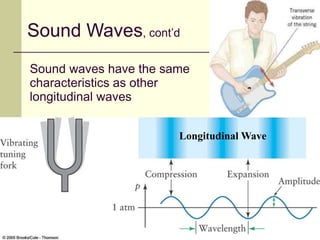
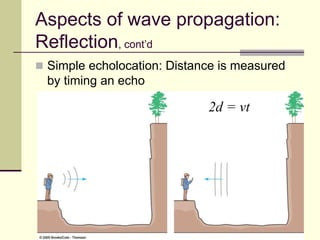
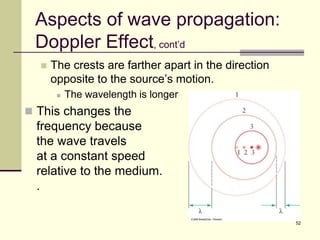
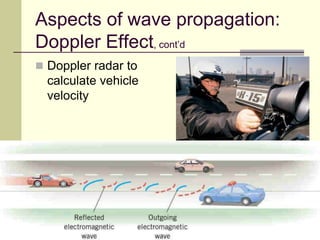
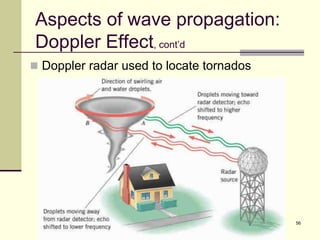
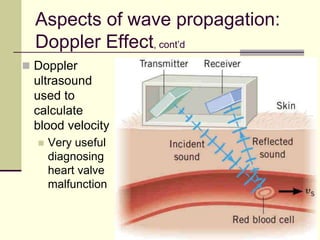
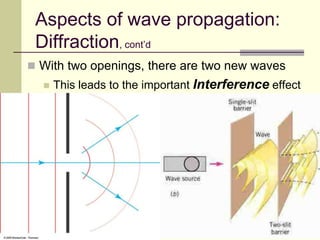
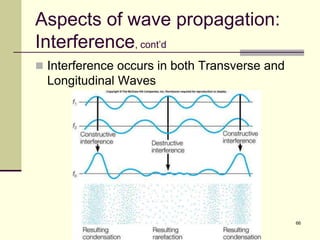
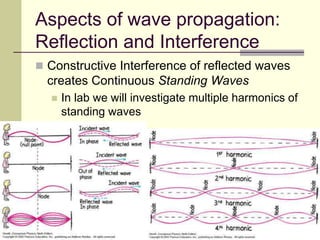
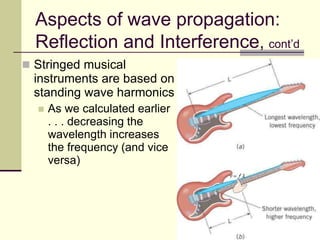
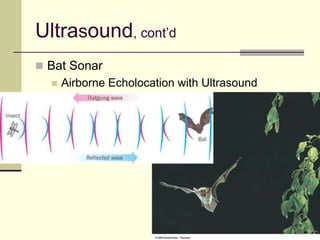
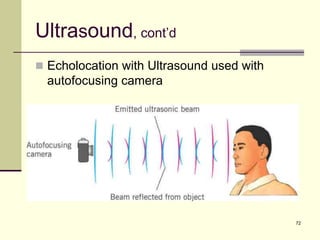
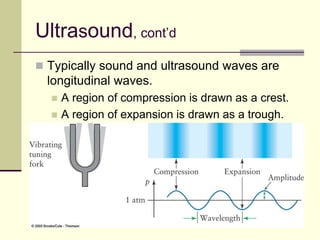
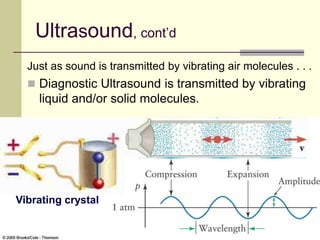
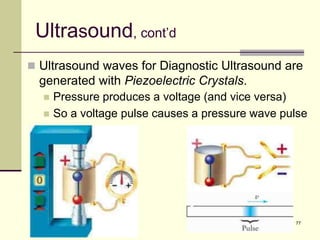
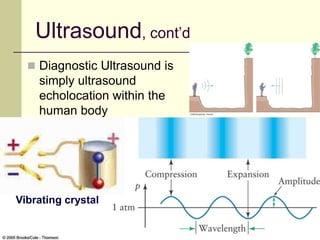
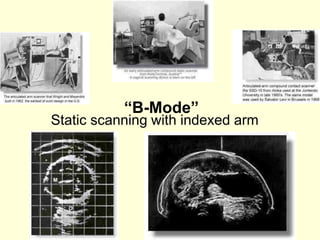
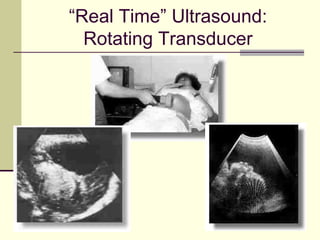
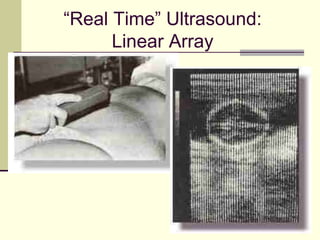
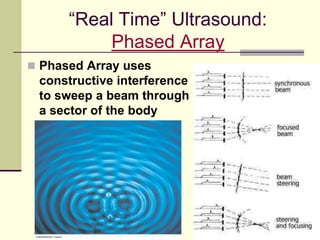
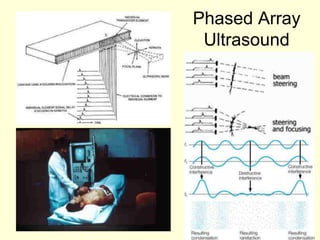
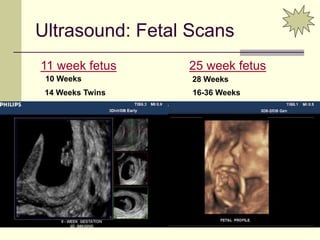
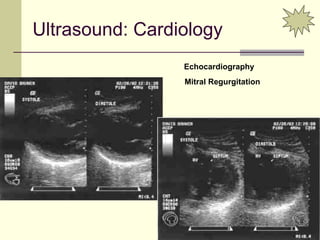
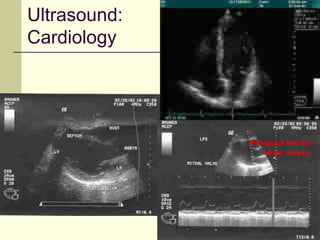
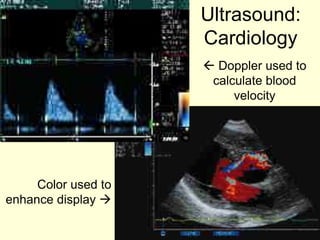
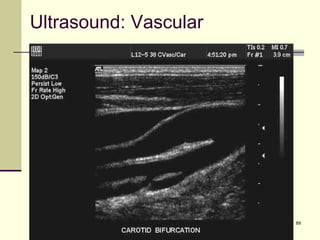
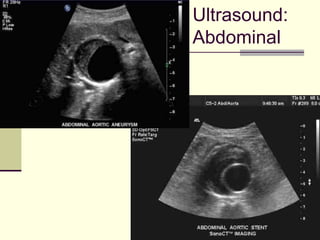
This document provides an overview of PHY 110 Introduction to Physics taught by Dr. Henry. It outlines the course content for the rest of the semester, which will cover chapters on waves, electricity, electromagnetism, atomic physics, nuclear physics, and special relativity. It then summarizes key concepts about waves, including the properties of transverse and longitudinal waves. It discusses sound as a longitudinal wave and provides the formula for the speed of sound. The document concludes by covering various aspects of wave propagation such as reflection, the Doppler effect, shock waves, diffraction, and interference.

1. PHY 110, Introduction to Physics
Dr. Henry
SC 453, 572-6164 (alt 572-5309)
E-Mail: henryh1@nku.edu
Web Site: www.nku.edu/~henryh1/
© Hugh Henry, 2008

2. If you are Tardy
Initial beside Your Name on the
Sheet on the Front Table

3. 3
The rest of the semester . . .
• Chapter 6, Waves and Sound (6.1-6.3)
• Chapter 7, Electricity (except Static
Electricity)
• Chapter 8, Electromagnetism and EM
Waves (8.1-8.6)
• Skip Chapter 9
• Chapter 10, Atomic Physics (10.1-10.2,
10.4-10.6)
• Chapter 11, Nuclear Physics (11.1-11.4)
• Chapter 12, Special Relativity and
Cosmology (12.1)

4. Chapter 6
(Sections 6.1-6.3)
Waves
A wave is a traveling disturbance consisting of
coordinate vibrations that transmit energy with
no net movement of matter.

5. 5
Waves — types and properties
 A wave is a traveling disturbance consisting
of coordinate vibrations that transmit energy
with no net movement of matter.
 The disturbance is frequently called an
oscillation or vibration.
 The substance through which the wave travels
is called the medium.

6. 6
Waves — types and properties,
cont’d
 There are two main wave types:
 Transverse waves have oscillations that are
perpendicular (transverse) to the direction the
wave travels.
 Examples include waves on a rope,
electromagnetic waves and some seismic waves.
 Longitudinal waves have oscillations that are
along the direction the wave travels.
 Examples include sound and some
seismic waves.

7. 7
Sound
© Hugh Henry, 2008
Transverse Waves
The_Nature_of_Waves

8. 8
Longitudinal Waves
(Sound and Ultrasound)
Sound_Waves

9. 9
Waves — types and properties,
cont’d
 This figure illustrates the two main types of
waves.
Longitudinal Wave
Transverse Wave

10. 10
Pulse
Wave
Continuous
Wave
Waves — types and properties,
cont’d

11. 11
Waves — types and properties,
cont’d
Both Types of Waves have similar properties
 Transverse Waves can be pulsed or
continuous

12. 12
Waves — types and properties,
cont’d
Both Types of
Waves have
similar properties
 Longitudinal
Waves can be
pulsed or
continuous

13. 13
Waves — types and properties:
Amplitude
 The amplitude of a wave is the maximum
displacement of the wave from the
equilibrium position.
 It is the distance equal to the height of a peak
or the depth of a valley (relative to the center).

14. 14
High Amplitude Waves
Low Amplitude Waves
Waves — types and properties:
Amplitude, cont’d

15. 15
Waves — types and properties:
Wavelength
 The wavelength is the distance between
successive “like” points on a wave.
 “Like” points might be peaks, valleys, etc.
 The wavelength is denoted by the lower case
Greek letter lambda: l.

16. 16
Waves — types and properties :
Wavelength, cont’d
 The wavelength is the
distance between successive
“like” points on a wave.
 Distance between ripples
passing a bird on a branch
 Distance between fronts of
freight cars

17. 17
Waves — types and properties:
Amplitude and Wavelength
 Here is an illustration of
changing the wavelength
and/or amplitude.
 Lower amplitude implies
smaller height/depth.
 Shorter wavelength
implies more complete
waves “fit” in a given
distance.

18. 18
Waves — types and properties:
Amplitude and Wavelength, cont’d
 Longitudinal waves are described by different
terminology than “peaks” and “valleys.”
 A compression is where the medium is squeezed together.
 A expansion (or rarefaction) is where the medium is
spread apart.

19. 19
Waves — types and properties:
Frequency
 The frequency of a wave
indicates the number of cycles
of a wave that pass a given
point per unit time.
 It is the number of oscillations
per second.
 This has been discussed
already in chapter 1.

20. 20
Consider:
Ripples of a continuous
water wave pass by a plant
 If 5 ripples (cycles) pass by
in 1s
 Frequency (f) = 5 cycles/s
 f = 5 Hz
as
Waves — types
and properties:
Frequency, cont’d

21. Waves — types and properties:
Velocity, cont’d
 The velocity of the crest of a wave can be
calculated using the equations in chapter 1.
 This velocity is called Wave Velocity

22. Calculate velocity from Chapter 1 equations
 If the frequency is 5 Hz, the
time between ripples (the
period) is t = 1/5Hz = 0.2s
 If the distance between
ripples is 0.03 meters . . .
 v = d/t = 0.03m/0.2s
 = 0.15 m/s
Waves — types
and properties:
Velocity

23. Velocity can be expressed in another way :
 Since d = λ and f = 1/t
 Then v = d/t  v = df = fλ
 Note the calculations are
the same as the previous
slide:
v = f λ = (5/s)*(0.03m)
v = 0.15 m/s
Waves — types
and properties:
Velocity, cont’d

24. 24
Waves — types and properties:
Velocity, cont’d
 Hence wavelength and frequency are related
to the wave velocity according to the formula:
 v is the wave’s velocity,
 f is the wave’s frequency, and
 l is the wave’s wavelength.
 This is a general formula for wave velocity
that will be used for the rest of the course.

25. 25
Waves — types and properties:
Velocity, cont’d
There are other formulas for wave velocity
which apply to special situations
 Consider, for example, a stretched wire or
string, with a length l and mass m.
 When the string is under a tension T, the
wave travels at speed:
 r is the mass per unit length:

26. 26
Waves — types and properties,
Velocity, cont’d
 From this we see that the speed:
 Increases as the tension increases.
 The string has a greater restoring
force that attempts to straighten it out.
 Is faster for smaller strings.
 The string has less mass that has to
be moved by the restoring force.
 Is independent of the length.
 The speed depends on the mass per
length, not on the length.
 This explains stringed musical
instruments

27. 27
Waves — types and properties,
Velocity, cont’d
 Notes depend on frequency,
which depends on:
 String tension, T
 String size, r
 Wavelength, λ
 “L” in the illustration
and
Combining
these:

28. 28
Example
Example 6.1
A Slinky is stretched out on the floor to a length
of 2 meters. The force needed to keep the
Slinky stretched in measured and found to be
1.2 Newtons. The Slinky’s mass is 0.3 kg.
What is the speed of any wave sent down the
Slinky?

29. 29
ANSWER:
The problem gives us:
The linear mass density is
Example
Example 6.1

30. 30
ANSWER:
The wave speed is then
Example
Example 6.1

31. 31
Sound
Sound_Waves

32. 32
Sound is a longitudinal wave
produced when something vibrates
and causes nearby air molecules to
vibrate
Longitudinal Wave
Sound Waves

33. 33
Sound waves have the same
characteristics as other
longitudinal waves
Longitudinal Wave
Sound Waves, cont’d

34. 34
Speed of a Sound Wave in a gas
 depends on the density of the gas
 and on the pressure
 and the temperature
Sound
Waves,
cont’d

35. 35
Sound Waves, cont’d
Another special case equation . . .
 The speed of a sound wave in
air at a temperature T is given
by the formula:
 The temperature must be
expressed in Kelvin.

36. 36
Example
Example 6.2
What is the speed of sound in air at room
temperature (20ºC = 68ºF)?
Music Hall, Cincinnati

37. 37
ANSWER:
The problem gives us:
We need to convert this temperature from
Celsius to Kelvin:
The sound speed is then
Example
Example 6.2

38. 38
DISCUSSION:
The factor of 20.1 strictly applies to the
properties of air.
For other gases:
 Helium:
 Carbon dioxide:
The general equation is:
 Where k is a constant
Example
Example 6.2

39. 39
Example
Example 6.3
Before a concert, musicians in an orchestra tune
their instruments to the note A, which has a
frequency of 440 Hz. What is the wavelength of
this sound in air at room temperature (20oC)?
We just calculated
the speed of
sound at 20oC is
344 m/s.
Music Hall, Cincinnati

40. 40
ANSWER:
The problem gives us:
The fundamental relation between frequency,
wavelength and wave speed is
The wavelength is then
Example
Example 6.3

41. Aspects of Wave
Propagation
Wave_Interference

42. 42
Aspects of wave propagation
Note in the graphics that follow . . .
 There are two ways to represent wave travel.
 A wavefront is a series of circles representing
the location of wave peaks at a particular time.
 A ray is an arrow
representing the
direction that a
wave segment
is traveling.

43. 43
Aspects of wave propagation:
Reflection
 A reflection occurs when a wave abruptly
changes direction.
 A wave is reflected whenever it reaches a
boundary of its medium or encounters an
abrupt change in the properties of its
medium.

44. 44
Aspects of wave propagation:
Reflection, cont’d
 We can use either the ray or
wavefront model to examine
reflection from a flat mirror.
 The point behind the mirror
from which the reflection
appears to originate is called
the image.

45. 45
Aspects of wave propagation:
Reflection, cont’d
 For a curved surface, the reflections can be
focused to a point.
 Examples include satellite dishes, radar
receivers, etc.

46. 46
Aspects of wave propagation:
Reflection, cont’d
 Wave reflection
is especially
important as a
means to
measure
distance
 Radar, Sonar,
Diagnostic
Ultrasound
 This is called
Echolocation

47. 47
Aspects of wave propagation:
Reflection, cont’d
 Simple echolocation: Distance is measured
by timing an echo
2d = vt

48. 48
Aspects of wave propagation:
Reflection, cont’d
 Echolocation used for Radar
 developed just before World War II

49. 49
The Klystron, invented in 1938 at Stanford
University, made airborne radar possible
and helped win the Battle of Britain and the U-Boat war

50. 50
Aspects of wave propagation:
Reflection, cont’d
 Sonar is Underwater Echolocation
 Sound Waves sent and reflected through water

51. 51
Aspects of wave propagation:
Doppler Effect
 The Doppler effect is a change in a wave’s
wavelength due to the relative motion between
the source and receiver.
 Consider a source
emitting waves and
moving to the right.
 The crests are closer
together in the direction
the source moves.
 The wavelength is shorter

52. 52
Aspects of wave propagation:
Doppler Effect, cont’d
 The crests are farther apart in the direction
opposite to the source’s motion.
 The wavelength is longer
 This changes the
frequency because
the wave travels
at a constant speed
relative to the medium.
.

53. 53
 Because of the Doppler Effect, each
listener hears the sound with a higher
or lower frequency (due to a longer or
shorter wavelength: v = fλ)
Aspects of wave propagation:
Doppler Effect, cont’d

54. 54
The Doppler Effect is the same with a moving
listener and stationary sound source OR a
stationary listener and moving sound source

55. 55
Aspects of wave propagation:
Doppler Effect, cont’d
 Doppler radar to
calculate vehicle
velocity

56. 56
Aspects of wave propagation:
Doppler Effect, cont’d
 Doppler radar used to locate tornados

57. 57
Aspects of wave propagation:
Doppler Effect, cont’d
 Doppler
ultrasound
used to
calculate
blood velocity
 Very useful
diagnosing
heart valve
malfunction

58. 58
Aspects of wave propagation:
Shock Wave
 A shock wave occurs whenever the speed of the source
is greater than the wave speed.
 The medium cannot respond fast enough to propagate
the wave, and the crests essentially “pile up.”
 This build-up causes a large-amplitude pulse: a sonic
boom for supersonic aircraft.
 Watching the waves expand
from the source over time, we
can construct a leading edge for
the shock wave.
 The angle of this leading-
edge led to delta-wing
configurations.

59. 59
Aspects of wave propagation:
Diffraction
 Diffraction results whenever a wave has to
travel past a barrier or obstruction.
 As the wave travels through the opening, the
outgoing waves bend.
 The amount of diffraction
depends on the wavelength
and the size of the
obstruction.

60. 60
Aspects of wave propagation:
Diffraction, cont’d
 When the opening is much larger than the
wavelength, there is little diffraction.
 The amount of diffraction increases as the
wavelength
becomes more
similar to the
size of the
opening.

61. 61
Aspects of wave propagation:
Diffraction, cont’d
 Diffraction explains why you
can hear a sound through a
door even if you’re behind a
wall.
 The sound’s wavelength is much
longer than the size of the door, so
the sound wave bends around the
wall.
 For the same reason . . . you can’t
see light around a door because the
wavelength is much shorter than
the size of the door.

62. 62
Aspects of wave propagation:
Diffraction, cont’d
 With two openings, there are two new waves
 This leads to the important Interference effect

63. 63
Aspects of wave propagation:
Interference
 Interference occurs whenever two or more
waves overlap.
 Their amplitudes add (or subtract) creating
new waveforms with amplified maxima and
minima

64. 64
Aspects of wave propagation:
Interference, cont’d
 When the waves
interfere to create a
larger amplitude, we
call it constructive
interference.
 When the waves
interfere to reduce
the amplitude, it is
called destructive
interference.

65. 65
Aspects of wave propagation:
Interference, cont’d
 Examples of Interference for a double slit
barrier with light waves (left) and with two
overlapping water waves (right).
 Note formation of new maxima and minima

66. 66
Aspects of wave propagation:
Interference, cont’d
 Interference occurs in both Transverse and
Longitudinal Waves

67. 67
Aspects of wave propagation:
Reflection and Interference
 Constructive Interference of reflected waves
creates Continuous Standing Waves
 In lab we will investigate multiple harmonics of
standing waves

68. 68
Aspects of wave propagation:
Reflection and Interference, cont’d
 Stringed musical
instruments are based on
standing wave harmonics
 As we calculated earlier
. . . decreasing the
wavelength increases
the frequency (and vice
versa)

69. Sound and Ultrasound
 The human hear can typically “hear” sounds
with frequencies in the range 20-20,000 Hz.
 Sound with frequencies below our audible
range is called infrasound.
 Below about 20 Hz.
 Sound with frequencies above our audible
range is called ultrasound.
 Above about 20,000 Hz.

70. Ultrasound
High Frequency Sound

71. 71
Ultrasound, cont’d
 Bat Sonar
 Airborne Echolocation with Ultrasound

72. 72
Ultrasound, cont’d
 Echolocation with Ultrasound used with
autofocusing camera

73. 73
Ultrasound Velocity
 The speed of sound and
ultrasound in a substance
depends on:
 the mass of its constituent
atoms
 the strength of the forces
between the atoms.
 Note the how close water is to
human tissue
 This is why “water phantoms”
have been used to calibrate
for radiation and ultrasound.

74. Medical Ultrasound
Sound with frequencies above
our audible range (~20,000 Hz)
is called ultrasound
Imaging_Technology___Ultrasound

75. 75
Ultrasound, cont’d
 Typically sound and ultrasound waves are
longitudinal waves.
 A region of compression is drawn as a crest.
 A region of expansion is drawn as a trough.

76. 76
Ultrasound, cont’d
Just as sound is transmitted by vibrating air molecules . . .
 Diagnostic Ultrasound is transmitted by vibrating
liquid and/or solid molecules.
Vibrating crystal

77. 77
Ultrasound, cont’d
 Ultrasound waves for Diagnostic Ultrasound are
generated with Piezoelectric Crystals.
 Pressure produces a voltage (and vice versa)
 So a voltage pulse causes a pressure wave pulse

78. 78
Ultrasound, cont’d
 Diagnostic Ultrasound is
simply ultrasound
echolocation within the
human body
Vibrating crystal

79. “B-Mode”
Static scanning with indexed arm

80. 80
Ultrasound, cont’d
“Real Time” Ultrasound
Linear Array
Rotating Transducer
Phased Array
with or without Doppler

81. 81
“Real Time” Ultrasound:
Rotating Transducer

82. 82
“Real Time” Ultrasound:
Linear Array

83. 83
“Real Time” Ultrasound:
Phased Array
 Phased Array uses
constructive interference
to sweep a beam through
a sector of the body

84. 84
Phased Array
Ultrasound

85. 85
Ultrasound: Fetal Scans
11 week fetus 25 week fetus
10 Weeks
14 Weeks Twins
28 Weeks
16-36 Weeks

86. 86
Ultrasound: Cardiology
Echocardiography
Mitral Regurgitation

87. 87
Ultrasound:
Cardiology
Doppler line for
blood velocity

88. 88
 Doppler used to
calculate blood
velocity
Color used to
enhance display 
Ultrasound:
Cardiology

89. 89
Ultrasound: Vascular

90. 90
Ultrasound:
Abdominal

91. 91
Important Equations
2d = vt Echolocation Equation

92. END