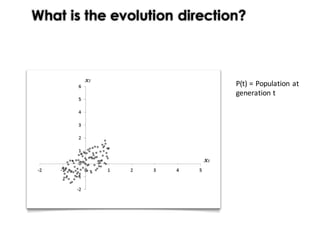
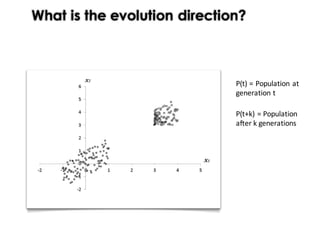
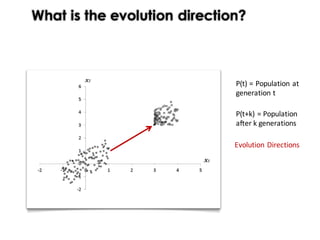
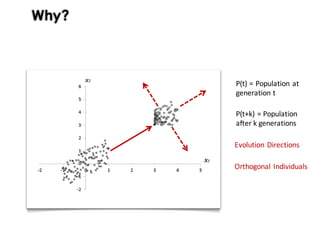
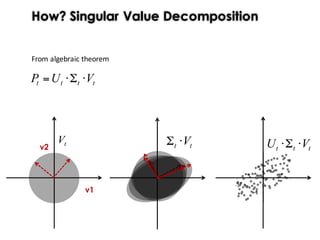
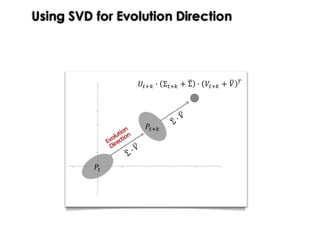
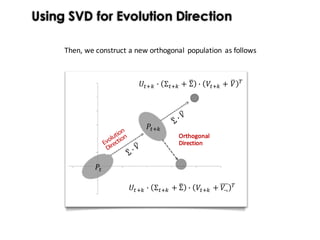
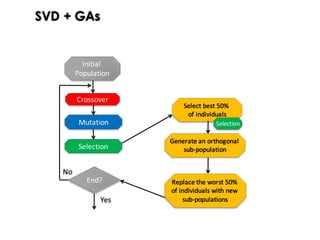
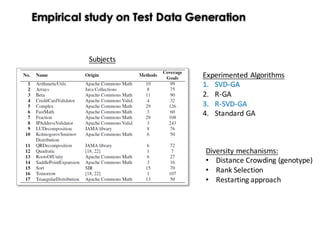
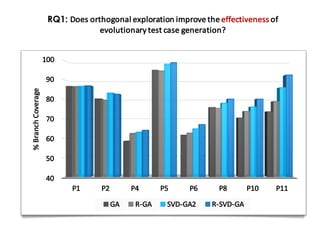
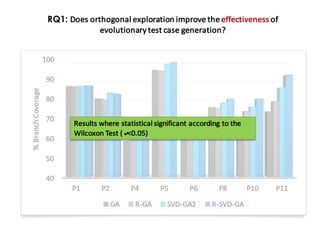
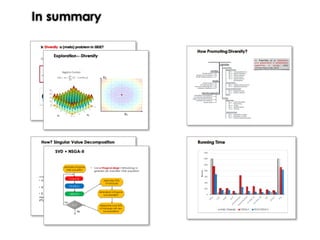
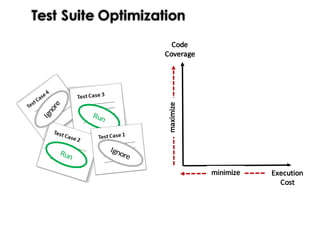
This document discusses mechanisms for maintaining diversity in evolutionary algorithms. It begins by explaining the importance of balancing exploration and exploitation. Several techniques for preserving diversity are then presented, including modifying genetic operators, changing the objective function, and applying statistical methods. Empirical evaluations demonstrate how diversity mechanisms can improve performance in search-based software engineering problems like test data generation and test suite optimization, which often suffer from premature convergence and getting stuck in local optima due to loss of diversity. Parameter tuning techniques like adjusting the mutation rate and niching methods like fitness sharing are also described as ways to explicitly promote diversity.

1. Diversity mechanisms for
evolutionary populations in
Search-Based Software
Engineering
Prof. Andrea De Lucia, University of Salerno, Italy
Dr. Annibale Panichella, FBK, Italy

2. Exploration vs. Exploitation
Exploration and Exploitation via Genetic Operators
Problem of Genetic Drift
Preserving Diversity Mechanism
Change the Genetic Operators
Add/Modify Objective Function
Apply Statistical Methods
Empirical Evaluation
Diversity in Test Data Generation
Diversity in Test Suite Optimization

3. Optimization Problems
Local Optimum
Global Optimum
Minimize
x
f(x)
Single-Objective Problem Multi-Objective Problem
Minimize
Minimize
f2(x)
f1(x)

4. General Process
Genetic Algorithms
Single-Objective GAs Multi-Objective GAs
• Roulette wheel
• Tournament
• Rank Scaling
• …
• Single-point
• Two-points
• Arithmetic
• …
• Uniform
• Bit-flip
• Adaptive
• …
Initial
Population
Crossover
Mutation
Selection
No
Yes
End?
• Non-dominated Sorting
• Epsilon Dominance
• Lorentz Dominance
• Single-point
• Two-points
• Arithmetic
• …
• Uniform
• Bit-flip
• Adaptive
• …

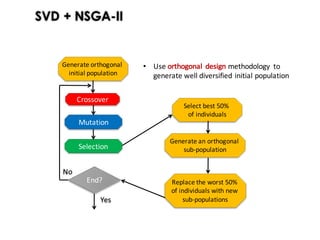
5. Key factors for GAs
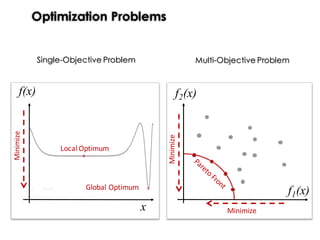
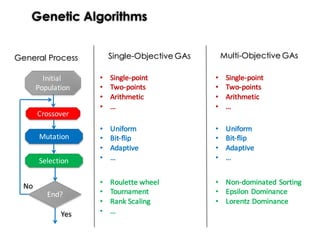
“Genetic Algorithms (GAs) must maintain a balance between the
exploitation […] and the exploration […] as to increase the probability of
finding the optimal solution.” Wong et al. [2003]
Exploitation: find nearby better solutions by promoting beneficial aspects
(genes) of existing solutions.
Exploration: find new solutions in different regions of the search space by
generating solutions with new aspects

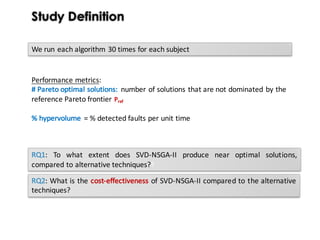
6. Key factors for GAs
“Genetic Algorithms (GAs) must maintain a balance between the
exploitation […] and the exploration […] as to increase the probability of
finding the optimal solution.” Wong et al. [2003]
Exploitation: find nearby better solutions by promoting beneficial aspects
(genes) of existing solutions. It is guaranteed by:
• Selection: it selects the fittest individuals for reproduction
• Crossover: it generate new nearby solutions
Exploration: find new solutions in different regions of the search space by
generating solutions with new aspects. It is guaranteed by:
• Mutation: it randomly modifies individuals with a given probability, and
thus increases the structural diversity of a population.

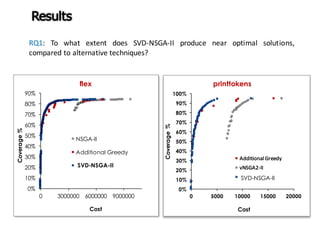
7. 0.5
1.5
0.5
1.5
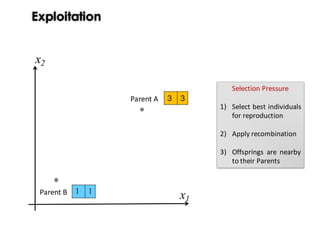
Exploitation
Selection Pressure
To find nearby better
solutions using crossover
and selection.
( ) ]2;0[,1)1(sin)(min 8
∈+−= xxxf
x
f(x)

8. Exploitation
Selection Pressure
1) Select best individuals
for reproduction
2) Apply recombination
3) Offsprings are nearby
to their Parents
Parent A
Parent B
x1
x2

9. Exploitation
Parent A
Parent B
x1
x2
Selection Pressure
1) Select best individuals
for reproduction
2) Apply recombination
3) Offsprings are nearby
to their Parents
Single Point crossover

10. Exploitation
Parent A
Parent B
x1
x2
Selection Pressure
1) Select best individuals
for reproduction
2) Apply recombination
3) Offsprings are nearby
to their Parents
Arithmetic crossover
2 2

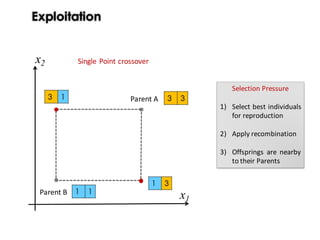
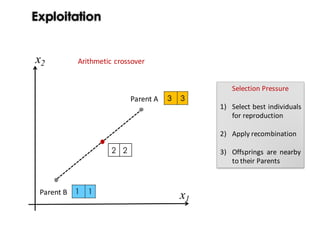
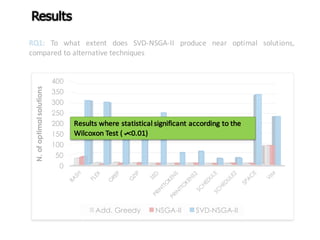
11. Exploration
GA got you
from here…
x
f(x)
( ) ]3.2;0[,1)1(sin)(min 8
∈+−= xxxf

12. Exploration
GA got you
from here…
( ) ]3.2;0[,1)1(sin)(min 8
∈+−= xxxf
Exploration
Looking for new
unexplored regions
x
f(x)

13. Exploration
GA got you
from here…
to here…
…but if you tried
something
radical…
( ) ]3.2;0[,1)1(sin)(min 8
∈+−= xxxf
x
f(x)

14. Exploration
GA got you
from here…
to here…
…but if you tried
something
radical…
…you could
get here!
( ) ]3.2;0[,1)1(sin)(min 8
∈+−= xxxf
x
f(x)

15. Exploration ←Diversity
Diversity is essential to
the genetic algorithm
because it enables the
algorithm to search a
larger region of the
space.
Low Diversity
High Diversity
x
f(x)

16. Exploration ←Diversity
Population driftx
f(x)
Diversity is essential to
the genetic algorithm
because it enables the
algorithm to search a
larger region of the
space.
Low Diversity
High Diversity

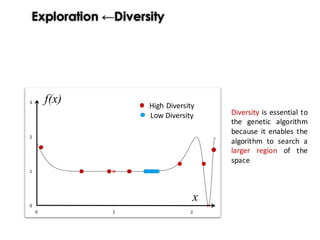
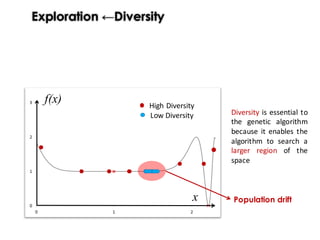
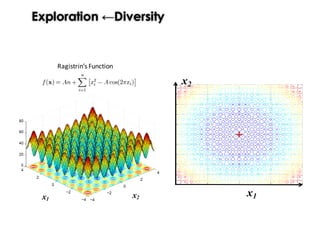
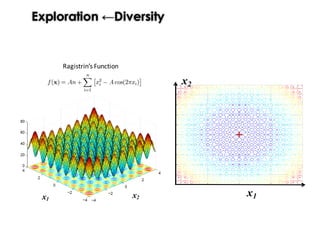
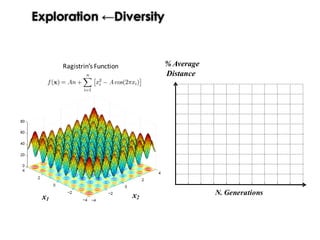
17. Exploration ←Diversity
“Progress in evolution depends fundamentally on the existence of variation of
population.”
“Unfortunately, a key problem in many Evolutionary Computation (EC) systems is
the loss of diversity through premature convergence. ”
McPhee and Hopper [2]
“This lack of diversity often leads to stagnation, as the system finds itself trapped
in local optima, lacking the genetic diversity needed to escape. ”

18. Exploration ←Diversity
x1
x2
Ragistrin’s Function
x1
x2

19. Exploration ←Diversity
x1
x2
Ragistrin’s Function
x1
x2

20. Exploration ←Diversity
x1
x2
Ragistrin’s Function
N. Generations
% Average
Distance

21. Is Diversity a (meta) problem in SBSE?
Consider two typical SEBSE applications:
Search-Based Test Data Generation
Multi-Objective Test Suite Optimization

22. public class Triangle {
public String check (double a, double b,
double c){
if(a == b)
{
if(a == c)
return ‘equilater’;
else
return ‘isoscele’;
}
else
{
if(a == c || b == c)
return ‘isoscele’;
else
return ‘scalene’;
}
}
}
1.
2.
3.
4.
5.
6.
7.
Search-Based Test Data Generation
Triangle Problem

23. public class Triangle {
public String check (double a, double b,
double c){
if(a == b)
{
if(a == c)
return ‘equilater’;
else
return ‘isoscele’;
}
else
{
if(a == c || b == c)
return ‘isoscele’;
else
return ‘scalene’;
}
}
}
1.
2.
3.
4.
5.
6.
7.
Triangle Problem
Search-Based Test Data Generation

24. public class Triangle {
public String check (double a, double b,
double c){
if(a == b)
{
if(a == c)
return ‘equilater’;
else
return ‘isoscele’;
}
else
{
if(a == c || b == c)
return ‘isoscele’;
else
return ‘scalene’;
}
}
}
1.
2.
3.
4.
5.
6.
7.
Triangle Problem
Search-Based Test Data Generation
Branch distance
(a == b) -> abs(a - b)
(a == c) -> abs(a – c))
min f(a,b,c) = 2 * abs(a - b) +
+ abs(a - c)

25. public class Triangle {
public String check (double a, double b,
double c){
if(a == b)
{
if(a == c)
return ‘equilater’;
else
return ‘isoscele’;
}
else
{
if(a == c || b == c)
return ‘isoscele’;
else
return ‘scalene’;
}
}
}
1.
2.
3.
4.
5.
6.
7.
Triangle Problem
Search-Based Test Data Generation
Test Case 4
Triangle t= new Triangle();
String s=t.check(2,2,2)
Branch distance
(a == b) -> abs(a - b)
(a == c) -> abs(a – c))
min f(a,b,c) = 2 * abs(a - b) +
+ abs(a - c)

26. c=2 a, b ϵ [-1;4]
a
b
Fitness
1) Flat seach space
2) Several Local optimal
3) Only one global optimum
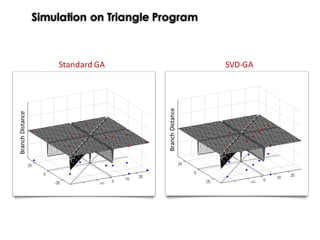
Triangle Problem
Search-Based Test Data Generation

27. a, b ϵ [-30;30]
c=2
a
b
Fitness
GAs Simulation
Mutation Rate = 0.10
Population = 50
Crossover = single-point
Premature convergence
(genetic drift)

28. Is Diversity a (meta) problem in SBSE?
Consider two typical SEBSE applications:
Search-Based Test Data Generation
Multi-Objective Test Suite Optimization

29. Regression Testing
Software before changes Software after changes

30. Regression Testing
Software before changes Software after changes
Test Case 1
Test Case 2
Test Case 3
Test Case n
Test Case 1
Test Case 2
Test Case 3
Test Case n
… …

31. Regression Testing is time consuming
1000 machine-hours
to execute 30,000
functional test cases
for a software
product…
Mirarab, et al. The effects of time constraints on test case prioritization:
A series of controlled experiments. TSE 2010

32. Test Suite Optimization
Code
Coverage
Execution
Cost
minimizemaximize

33. Multi-Criteria Regression Testing
Multi-Objective Paradigm
Multiple otpimal solutions can be
found

34. Multi-Criteria Regression Testing
There is no clear winner between MOGAs and Greedy Algorithms

35. Multi-Criteria Regression Testing
There is no clear winner between MOGAs and Greedy Algorithms
Population drift. GA can converge toward sub-optimal Pareto fronts

36. Diversity

37. How Promoting Diversity?
M. Črepinšek, et al. Exploration
and exploitation in evolutionary
algorithms: A survey. ACM
Computing Survey. 2013

38. How Promoting Diversity?
M. Črepinšek, et al. Exploration
and exploitation in evolutionary
algorithms: A survey. ACM
Computing Survey. 2013

39. How Promoting Diversity?
1. Parameter tuning
M. Črepinšek, et al. Exploration
and exploitation in evolutionary
algorithms: A survey. ACM
Computing Survey. 2013

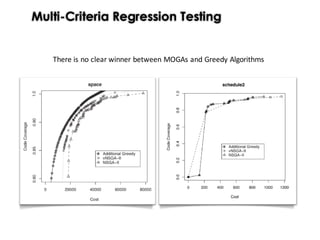
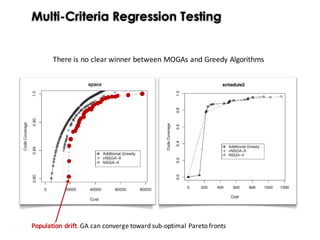
40. Mutation Rate
Peaks Funtcion
x1
x2
f(x)
Mutation Type = uniform
Mutation Rate = 0.01
Population Size =50
Crossover = Single-point
Crossover prob. = 0.6
Selection = roulette wheel
[Whitley and Starkweather 1990]

41. Mutation Rate
Peaks Funtcion
x1
x2
f(x)
Exploitation
Exploration
Sub-optimal
solutions
can be reached
Mutation Type = uniform
Mutation Rate = 0.01
Population Size =50
Crossover = Single-point
Crossover prob. = 0.6
Selection = roulette wheel
[Whitley and Starkweather 1990]

42. Mutation Rate
Peaks Funtcion
x1
x2
f(x)
GAs might remain
at certain distance
to the optimum
Exploitation
Exploration
Mutation Type = uniform
Mutation Rate = 0.90
Population Size =50
Crossover = Single-point
Crossover prob. = 0.6
Selection = roulette wheel
[Whitley and Starkweather 1990]

43. Mutation Rate
Peaks Funtcion
x1
x2
f(x)
GAs might remain
at certain distance
to the optimum
Exploitation
Exploration
Mutation Type = uniform
Mutation Rate = 0.90
Population Size =50
Crossover = Single-point
Crossover prob. = 0.6
Selection = roulette wheel
[Whitley and Starkweather 1990]

44. How Promoting Diversity?
M. Črepinšek, et al. Exploration
and exploitation in evolutionary
algorithms: A survey. ACM
Computing Survey. 2013
1. Parameters tuning
2. Niching Schema

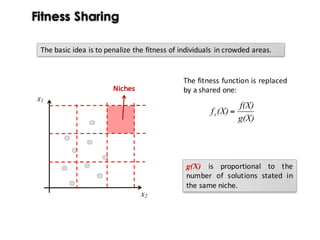
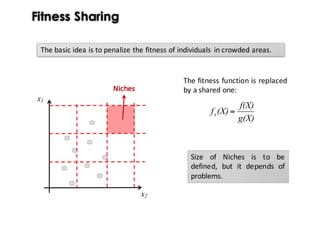
45. Fitness Sharing
x1
x2
The basic idea is to penalize the fitness of individuals in crowded areas.
1) Divide the search space in partitions
or segments
2) Measure how scattered the
solutions are across the identified
partitions
3) Encourage individuals stated in
partitions sparely populated and
penalize individuals stated in
partitions densely populated
Niches
[Holland 1975]
[Goldberg and Richardson 198]

46. Fitness Sharing
g(X)
f(X)
(X)fs =
g(X) is proportional to the
number of solutions stated in
the same niche.
x1
x2
The basic idea is to penalize the fitness of individuals in crowded areas.
Niches
The fitness function is replaced
by a shared one:

47. Fitness Sharing
Size of Niches is to be
defined, but it depends of
problems.
g(X)
f(X)
(X)fs =
x1
x2
The basic idea is to penalize the fitness of individuals in crowded areas.
Niches
The fitness function is replaced
by a shared one:

48. How Promoting Diversity?
M. Črepinšek, et al. Exploration
and exploitation in evolutionary
algorithms: A survey. ACM
Computing Survey. 2013
1. Parameters tuning
2. Niching Schema

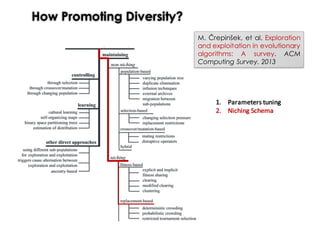
49. Crowding Distance
The most used diversity preserving techniques is the crowding distance.
x1
x2
A(a1,a2)
B(b1,b2)
[Mahfoud 1995]

50. Crowding Distance
x1
x2
It selects individuals that are distant from each other in the objectives
space.
( ) ( )
)B,A(
babaB)(A,d
babaB)(A,d
11
2
22
2
11
Hamming
222
1
−+−=
−+−=
Genotype
The independent variables
can have different ranges!
The most used diversity preserving techniques is the crowding distance.
x1
x2
A(a1,a2)
B(b1,b2)
[Mahfoud 1995]

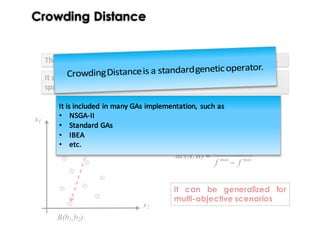
51. Crowding Distance
minmax
ff
f(B)f(A)
B)dc(A,
−
−
=
Phenotype
x1
x2
It selects individuals that are distant from each other in the objectives
space.
The most used diversity preserving techniques is the crowding distance.
x1
x2
A(a1,a2)
B(b1,b2)
It can be generalized for
multi-objective scenarios
[Mahfoud 1995]

52. Crowding Distance
minmax
ff
f(B)f(A)
B)dc(A,
−
−
=
Phenotype
x1
x2
It selects individuals that are distant from each other in the objectives
space.
The most used diversity preserving techniques is the crowding distance.
x1
x2
A(a1,a2)
B(b1,b2)
It can be generalized for
multi-objective scenarios
It is included in many GAs implementation, such as
• NSGA-II
• Standard GAs
• IBEA
• etc.

53. How Promoting Diversity?
M. Črepinšek, et al. Exploration
and exploitation in evolutionary
algorithms: A survey. ACM
Computing Survey. 2013
1. Parameters tuning
2. Niching Schema
3. Non-niching Schema

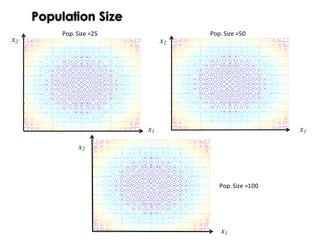
54. Population Size
The idea is to maintain diversity by varying the population size.
Steps:
1. Run GA with a given initial population size(PopSize=M)
2. Once GA converged storethe best solution
3. Increase PopSize=PopSize*2
4. Re-run with the new population size
5. Repeat steps 2-4 until the best solution is not improved for k re-runs
[McPhee and Hopper 1999]

55. Population Size
x1
x2
x1
x2
Pop. Size =25 Pop. Size =50
Pop. Size =100
x1
x2

56. Injection of new individuals
The idea is to maintain diversity by replacing identical individuals.
Variants:
1. Single generation: during each generation replace duplicated solutions
with new random ones (injection)
Issue: already explored individuals might be regenerated
2. Archive based: all individuals are stored in an archive of individuals
already explored; during each generation:
i. replace solutions already presents in the archive with new random
ones
ii. update archive
Issue: it requires to store all individuals (too memory)
[Chaiyaratana et al. 2007]
[Zhang and Sanderson 2009]

57. Sup-population with migration
Maintaining diversity by using sub-population (island GA)
x1
x2
Steps:
1. Split the search space in N sub-regions
(islands)
2. Run multiple GAs for each island
independently for k generations
3. Each k generations exchange the
populations between the different GAs
GA 1 GA 2
GA 3 GA 4
Island version of NSGA-II
(vNSGA-II) have been used
for test suite optimization

58. How Promoting Diversity?
M. Črepinšek, et al. Exploration
and exploitation in evolutionary
algorithms: A survey. ACM
Computing Survey. 2013
1. Parameters tuning
2. Niching Schema
3. Non-niching Schema
4. New objectives

59. Diversity as Objective function
Ask to GAs to optimize the diversity through adaptation
Genetic Algorithms
1. Minimize f(x) (objective)
2. Maintain diversity (genetic
operators)

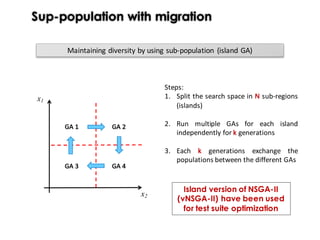
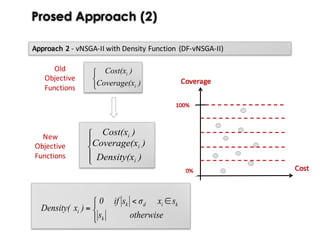
60. Diversity as Objective function
Ask to GAs to optimize the diversity through adaptation
Genetic Algorithms
1. Minimize f(x) (objective)
2. Maintain diversity (genetic
operators) (objective)
Multi-Objective Problem
min f(x)
min [f1(x),..., fn(x)]
min [f(x) d(x)]
min [f1(x) ... fn(x) d(x)]
Single-Objective Problem
d(x)= average similarity between
x and the other solutions

61. Density function in TSO
Multi-objective TSO Problem
Coverage
Cost0%
100%

62. Density function in TSO
Coverage
Cost0%
100%
For TCS problem each solution
ranges between 0% and 100% in
the coverage space
Multi-objective TSO Problem

63. Proposed Approach (2)
Coverage
Cost0%
100%
1) Divide the coverage space in k
partitions
2) Measure how scattered the
solutions are across the identified
partitions
3) Encourage individuals stated in
partitions sparely populated and
penalize individuals stated in
partitions densely populated

64. ⎩
⎨
⎧
)Coverage(x
)Cost(x
i
i
Prosed Approach (2)
⎪⎩
⎪
⎨
⎧
)Density(x
)Coverage(x
)Cost(x
i
i
i
Old
Objective
Functions
New
Objective
Functions
⎩
⎨
⎧ ∈<
=
otherwises
sxσsif0
)xDensity(
k
kidk
i
Coverage
0%
100%
Approach 2 - vNSGA-II with Density Function (DF-vNSGA-II)
Coverage
Cost0%
100%

65. 500 generations
0
10
20
30
40
50
60
70
80
90
100
0 300 600 900 1200 1500 1800
Coverage
Cost
vNSGA-II
DF-vNSGA-II
Convergence Analysis for space

66. 0
10
20
30
40
50
60
70
80
90
100
0 200 400 600 800
Coverage
Cost
vNSGA-II
DF-vNSGA-II
700 generations500 generations
0
10
20
30
40
50
60
70
80
90
100
0 300 600 900 1200 1500 1800
Coverage
Cost
vNSGA-II
DF-vNSGA-II
Convergence Analysis for space

67. 0
10
20
30
40
50
60
70
80
90
100
0 100 200 300 400
Coverage
Cost
vNSGA-II
DF-vNSGA-II
1,000 generations
0
10
20
30
40
50
60
70
80
90
100
0 200 400 600 800
Coverage
Cost
vNSGA-II
DF-vNSGA-II
700 generations500 generations
0
10
20
30
40
50
60
70
80
90
100
0 300 600 900 1200 1500 1800
Coverage
Cost
vNSGA-II
DF-vNSGA-II
Convergence Analysis for space

68. Diversity as Objective function
A. Toffolo and E. Benini. Genetic
diversity as an objective in multi-
objective evolutionary algorithms.
Evolutionary Computation, 2003
S. Watanabe, and K. Sakakibara, Multi-
objective approaches in a single-
objective optimization environment,
IEEE Congress on Evolutionary
Computation, 2005.
A. De Lucia, M. Di Penta, R. Oliveto, A.
Panichella, On the role of diversity
measure for multi-objective test case
selection, AST 2012.

69. How Promoting Diversity?
M. Črepinšek, et al. Exploration
and exploitation in evolutionary
algorithms: A survey. ACM
Computing Survey. 2013
1. Parameters tuning
2. Niching Schema
3. Non-niching Schema
4. New objectives
5. Statistic Approach

70. Injecting Diversity
Estimating the
Evolution Direction

71. What is the evolution direction?
P(t) = Population at
generation t

72. What is the evolution direction?
P(t) = Population at
generation t
P(t+k) = Population
after k generations

73. What is the evolution direction?
Evolution Directions
P(t) = Population at
generation t
P(t+k) = Population
after k generations

74. Why?
P(t) = Population at
generation t
P(t+k) = Population
after k generations
Evolution Directions
Orthogonal Individuals

75. How?
The basic idea is that a population of solutions P provided by GA at generation
t can be viewed as a m x n matrix
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
nmmm
n
n
ppp
ppp
ppp
P
,2,1,
,22,21,2
,12,11,1
!
"#""
!
! Individual 1
Individual 2
Individual m

76. It measures the
relationship between
genes within the
individuals space
Eigenvalues and Eigenvectors
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=⋅
nmmm
n
n
nmnn
m
m
T
aaa
aaa
aaa
aaa
aaa
aaa
AA
,2,1,
,22,21,2
,12,11,1
,,2,1
2,2,22,1
1,1,21,1
!
"#""
!
!
!
"#""
!
!
It measures the
relationship between
factors within the
observations space
The eigenvectors of (P PT) form an orthogonal basis of the space Rm
Each gene of P can be expressed as linear combination of
U={u1, u2, …, um}
{ } 0and,,,)( 21 =×=⋅ T
jim
T
uuuuuPPrsEigenVecto !
It measures the
relationship between
individuals within the
genotype space⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=⋅
nmnn
m
m
nmmm
n
n
T
ppp
ppp
ppp
ppp
ppp
ppp
PP
,,2,1
2,2,22,1
1,1,21,1
,2,1,
,22,21,2
,12,11,1
!
"#""
!
!
!
"#""
!
!

77. It measures the
relationship between
individuals within the
genotype space
Eigenvalues and Eigenvectors
It measures the
relationship between
observations within the
factors space
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=⋅
nmnn
m
m
nmmm
n
n
T
aaa
aaa
aaa
aaa
aaa
aaa
AA
,,2,1
2,2,22,1
1,1,21,1
,2,1,
,22,21,2
,12,11,1
!
"#""
!
!
!
"#""
!
!The eigenvectors of (PT P) form an orthogonal basis of the space Rn
Each individual of P can be expressed as linear combination of
V={v1, v2, …, vm}
{ } 0and,,,)( 21 =×=⋅ T
jin
T
vvvvvPPrsEigenVecto !
It measures the
relationship between
genes within the
individuals space⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=⋅
nmmm
n
n
nmnn
m
m
T
ppp
ppp
ppp
ppp
ppp
ppp
PP
,2,1,
,22,21,2
,12,11,1
,,2,1
2,2,22,1
1,1,21,1
!
"#""
!
!
!
"#""
!
!

78. How? Singular Value Decomposition
THEOREM: Let P be a mxn matrix with rank k. There are three matrix U Σ V such that
VUP nkkkkmnm ××××
⋅⋅= Σ
Where:
• U contains the left singular vectors of P.They are eigenvectors of (PT P).
• V contains the right singular vectors of P. They are eigenvectors of (P PT ) .
• Σ is a diagonal matrix containing the non-zero singular values of P (found on the diagonal
entries of Σ) are the square roots of the non-zero eigenvalues of both (PT P) (P PT).

79. From algebraic theorem
tttt VUP ⋅Σ⋅=
tt V⋅ΣtV
v2
v1
How? Singular Value Decomposition
ttt VU ⋅Σ⋅

80. Population at generation t
tP ktP+
How? Singular Value Decomposition
Population at generation t Population at generation t + k

81. Population at generation t
We can compute two SVD
decompositions
tttt VUP ⋅Σ⋅=
Population at generation t + k
ktktktkt VUP ++++ ⋅Σ⋅=
v2
v1
v1
v2
How? Singular Value Decomposition

82. The currect evolution direction is related to
v2
v1
v1
v2
By definition V is a Rotating operator
By definition Σ is a scaling operator
Σ
How? Singular Value Decomposition
v1
v2

83. Using SVD for Evolution Direction
𝑈"#$ % Σ"#$ + Σ( % 𝑉"#$ + 𝑉( *
𝑃"#$
𝑃"

84. Using SVD for Evolution Direction
𝑈"#$ % Σ"#$ + Σ( % 𝑉"#$ + 𝑉( *
𝑃"#$
𝑃"

85. Using SVD for Evolution Direction
Then, we construct a new orthogonal population as follows
𝑈"#$ % Σ"#$ + Σ( % 𝑉"#$ + 𝑉( *
𝑃"#$
𝑃"
𝑈"#$ % Σ"#$ + Σ( % 𝑉"#$ + 𝑉¬
*
Orthogonal
Direction

86. Integration SVD with Standard GA
• Rank Scaling Selection
• Single-point crossover
• Uniform mutation
Initial
Population
Crossover
Mutation
Selection
No
Yes
End?

87. Select best 50%
of individuals
Generate an orthogonal
sub-population
Replace the worst 50%
of individuals with new
sub-populations
SVD + GAs
Initial
Population
Crossover
Mutation
Selection
No
Yes
End?
Selection

88. Diversity in SBSE
Consider two typical SEBSE applications:
Search-Based Test Data Generation
Multi-Objective Test Suite Optimization

89. Simulation on Triangle Program
SVD-GAStandard GA
Branch Distance
Branch Distance

90. Empirical study on Test Data Generation
Subjects
Experimented Algorithms:
1. SVD-GA
2. R-GA
3. R-SVD-GA
4. Standard GA
Diversity mechanisms:
• Distance Crowding (genotype)
• Rank Selection
• Restarting approach

91. Experimented algorithms
Parameter settings:
• Population size: 50 individuals
• Stop condition: maximum number of 10E+6 executed statements or a
maximum of 30 minutes of computation time
• Crossover: single point fixed crossover with probability Pc = 0.75
• Mutation: uniform mutation function with probability Pm =1/n
• Selection function: rank selection is used with bias = 1.7
We run each algorithm 100 times for each subject
Performance metrics:
Effectiveness = % covered branches
Efficiency/cost = # executed statements

92. Research Questions
RQ1: Does orthogonal exploration improve the effectiveness of
evolutionary test case generation?
RQ2: Does orthogonal exploration improve the efficiency of
evolutionary test case generation?

93. 40
50
60
70
80
90
100
P1 P2 P4 P5 P6 P8 P10 P11
% Branch Coverage
GA R-GA SVD-GA2 R-SVD-GA
RQ1: Does orthogonal exploration improve the effectiveness of
evolutionary test case generation?

94. 40
50
60
70
80
90
100
P1 P2 P4 P5 P6 P8 P10 P11
% Branch Coverage
GA R-GA SVD-GA2 R-SVD-GA
RQ1: Does orthogonal exploration improve the effectiveness of
evolutionary test case generation?
Results where statistical significant according to the
Wilcoxon Test (a<0.05)

95. 0
10
20
30
40
50
60
70
80
P10 P12 P13 P14
Cost (#Exec. Statements)
GA R-GA SVD-GA R-SVD-GA
RQ2: Does orthogonal exploration improve the efficiency of
evolutionary test case generation?
0
100
200
300
400
500
600
P7 P8 P15 P16
Cost (#Exec. Statements)
GA R-GA SVD-GA R-SVD-GA

96. 0
10
20
30
40
50
60
70
80
P10 P12 P13 P14
Cost (#Exec. Statements)
GA R-GA SVD-GA R-SVD-GA
RQ2: Does orthogonal exploration improve the efficiency of
evolutionary test case generation?
0
100
200
300
400
500
600
P7 P8 P15 P16
Cost (#Exec. Statements)
GA R-GA SVD-GA R-SVD-GA
Results where statistical significant according to the
Wilcoxon Test (a<0.05)

97. Estimating the Evolution Direction of Populations
to Improve Genetic Algorithms. A. De Lucia , M.
Di Penta, R. Oliveto, A. Panichella
GECCO 2012
Orthogonal exploration
Orthogonal Exploration of the Search Space in
Evolutionary Test Case Generation F. M. Kifetew,
A. Panichella , A. De Lucia , R. Oliveto, P. Tonella
ISSTA 2013

98. Diversity in SBSE
Consider two typical SEBSE applications:
Search-Based Test Data Generation
Multi-Objective Test Suite Optimization

99. Diversity Injection in NSGA-II
• Non Dominated Sorting Algorithm
• Crowding Distance
• Tournament Selection
• Multi-points crossover
• Bit-flip mutation
Initial
Population
Crossover
Mutation
Selection
No
Yes
End?

100. Diversity Injection in NSGA-II
Yes
Generate orthogonal
initial population
• Use orthogonal design methodology to
generate well diversified initial population
population
Crossover
Mutation
Selection
No
Yes
End?

101. SVD + NSGA-II
Select best 50%
of individuals
Generate an orthogonal
sub-population
Replace the worst 50%
of individuals with new
sub-populations
• Use orthogonal design methodology to
generate well diversified initial population
Generate orthogonal
initial population
Crossover
Mutation
Selection
No
Yes
End?

102. Empirical Evaluation
Experimented Algorithms:
1. SVD-NSGA-II + Init. Pop
2. NSGA-II
3. Additional Greedy Algorithm
Problems:
1. 2-objectives
• Execution Cost
• Code Coverage
2. 3-objectives
• 2-objectives + Past Faults Coverage
Software systems:
Diversity mechanisms:
• Crowding Distance (phenotype + genotype)
• Tournament Selection
• Islands / sub-populations

103. Study Definition
We run each algorithm 30 times for each subject
Performance metrics:
# Pareto optimal solutions: number of solutions that are not dominated by the
reference Pareto frontier Pref
% hypervolume = % detected faults per unit time
RQ1: To what extent does SVD-NSGA-II produce near optimal solutions,
compared to alternative techniques??
RQ2: What is the cost-effectiveness of SVD-NSGA-II compared to the alternative
techniques?

104. 0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
0 3000000 6000000 9000000
Coverage%
Cost
flex
NSGA-II
Additional Greedy
DIV-GASVD-NSGA-II
Results
RQ1: To what extent does SVD-NSGA-II produce near optimal solutions,
compared to alternative techniques??
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
0 5000 10000 15000 20000
Coverage%
Cost
printtokens
Additional Greedy
vNSGA2-II
DIV-GASVD-NSGA-II

105. 0
50
100
150
200
250
300
350
400
N.ofoptimalsolutions
Add. Greedy NSGA-II SVD-NSGA-II
Results
RQ1: To what extent does SVD-NSGA-II produce near optimal solutions,
compared to alternative techniques?
Results where statistical significant according to the
Wilcoxon Test (a<0.01)

106. RQ2: What is the cost-effectiveness of SVD-NSGA-II compared to the alternative
techniques?
Results
space bash

107. RQ2: What is the cost-effectiveness of SVD-NSGA-II compared to the alternative
techniques?
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
%Detectedfaultsperunitcost
Add. Greedy NSGA-II SVD-NSGA-II
Results

108. RQ2: What is the cost-effectiveness of SVD-NSGA-II compared to the alternative
techniques?
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
%Detectedfaultsperunitcost
Add. Greedy NSGA-II SVD-NSGA-II
Results
Results where statistical significant according to the
Wilcoxon Test (a<0.01)

109. Running Time
0
200
400
600
800
1000
1200
1400Time(s)
Add. Greedy NSGA-II SVD-NSGA-II

110. Diversity in T.S. Optimization
On the role of diversity measures for multi-
objective test case selection. A. De Lucia, M. Di
Penta, R. Oliveto, A. Panichella. International
Workshop on Automation of Software Test (AST)
2012
Improving Multi-Objective Search Based Test
Suite Optimization through Diversity Injection. A.
Panichella, R. Oliveto, M. Di Penta, A. De Lucia. In
major revision at IEEE Transactions on Software
Engineering (TSE).

111. In summary

112. Bibliography
• A. De Lucia , M. Di Penta, R. Oliveto, A. Panichella, Estimating the Evolution Direction of
Populations to Improve Genetic Algorithm. GECCO 2012
• F. M. Kifetew, A. Panichella , A. De Lucia , R. Oliveto, P. Tonella, Orthogonal Exploration of the
Search Space in Evolutionary Test Case Generation, ISSTA 2013
• A. De Lucia, M. Di Penta, R. Oliveto, A. Panichella. On the role of diversity measures for multi-
objective test case selection. International Workshop on Automation of Software Test (AST)
2012.
• A. Panichella, R. Oliveto, M. Di Penta, A. De Lucia, Improving Multi-Objective Search Based Test
Suite Optimization through Diversity Injection. In major revision at IEEE Transactions on
Software Engineering (TSE).
• Wong et. al. A novel approach in parameter adaptation and diversity maintenance for genetic
algorithms. Soft Computing, 2003.
• M. Črepinšek, S. Liu, and M. Mernik. 2013. Exploration and exploitation in evolutionary
algorithms: A survey. ACM Computer Survey. 2013
• S. Watanabe, and K. Sakakibara, Multi-objective approaches in a single-objective optimization
environment, IEEE Congress on Evolutionary Computation, 2005.

113. Bibliography
• A. Toffolo and E. Benini. Genetic diversity as an objective in multi-objective evolutionary
algorithms. Evolutionary Computation, 2003
• P. Bosman, D. Thierens, The balance between proximity and diversity in multi-objective
evolutionary algorithms, IEEE Transactions on Evolutionary Computation, 2003
• X. Cui, M. Li, T. Fang, Study of population diversity of multi-objective evolutionary algorithm
based on immune and entropy principles, Proceedings of the Congress on Evolutionary
Computation, 2001.
• Mark Wineberg and Franz Oppacher, The Underlying Similarity of Diversity Measures Used in
Evolutionary Computation, GECCO 2013.
• S. Yoo and M. Harman, “Regression testing minimization, selection and prioritization: a survey,”
Softw. Test. Verif. Reliab., vol. 22, no. 2, pp. 67–120, Mar. 2012.
• M. J. Harrold, R. Gupta, and M. L. Soffa, “A methodology for controlling the size of a test suite,”
ACM Transactions Software Engineering and Methodologies, vol. 2, pp. 270–285, 1993.
• S. Yoo, M. Harman, and S. Ur, “Highly scalable multi objective test suite minimisation using
graphics cards,” in Proceedings of the Third international conference on Search based software
engineering. Springer-Verlag, 2011, pp. 219–236.

114. Bibliography
• S. Yoo and M. Harman, “Pareto efficient multi-objective test case selection,” in Proceedings of
the ACM/SIGSOFT International Symposium on Software Testing and Analysis. London, UK:
ACM Press, 2007, pp. 140–150
• H. Li, Y.-C. Jiao, L. Zhang, and Z.-W. Gu, “Genetic algorithm based on the orthogonal design for
multidimensional knapsack problems,” Advances in Natural Computation, vol. 4221, pp. 696–
705, 2006.
• R. T. Marler and J. S. Arora, “Survey of multi-objective optimization methods for engineering,”
Structural and Multidisciplinary Optimization, vol. 26, pp. 369–395, 2004.
• H. E. Aguirre and K. Tanaka, “Selection, drift, recombination, and mutation in multiobjective
evolutionary algorithms on scalable mnk-landscapes,” in Evolutionary Multi-Criterion
Optimization, ser. Lecture Notes in Computer Science, vol. 3410. Springer Berlin Heidelberg,
2005.
• K. Deb, A. Pratap, S. Agarwal, and T. Meyarivan, “A fast elitist multi-objective genetic algorithm:
NSGA-II,” IEEE Transactions on Evolutionary Computation, vol. 6, pp. 182–197, 2000.
• A. E. Eiben and C. A. Schippers, “On evolutionary exploration and exploitation,” Fundam.
Inform., vol. 35, no. 1-4, pp. 35–50, 1998.

115. Bibliography
• H. Maaranen, K. Miettinen, and A. Penttinen, “On initial populations of a genetic algorithm for
continuous optimization problems,” Journal of Global Optimization, vol. 37, no. 3, pp. 405–436,
Mar. 2007.
• J. Zhu, G. Dai, and L. Mo, “A cluster-based orthogonal multi-objective genetic algorithm,”
Computational Intelligence and Intelligent Systems, vol. 51, pp. 45–55, 2009.
• S. W. Mahfoud, “Niching methods for genetic algorithms,” Illinois Genetic Algorithms
Laboratory, Tech. Rep., 1995.
• G. Harik, “Finding multimodal solutions using restricted tournament selection,” in Proceedings
of the Sixth International Conference on Genetic Algorithms. Pittsburgh, PA, USA: Morgan
Kaufmann, 1995, pp. 24–31.