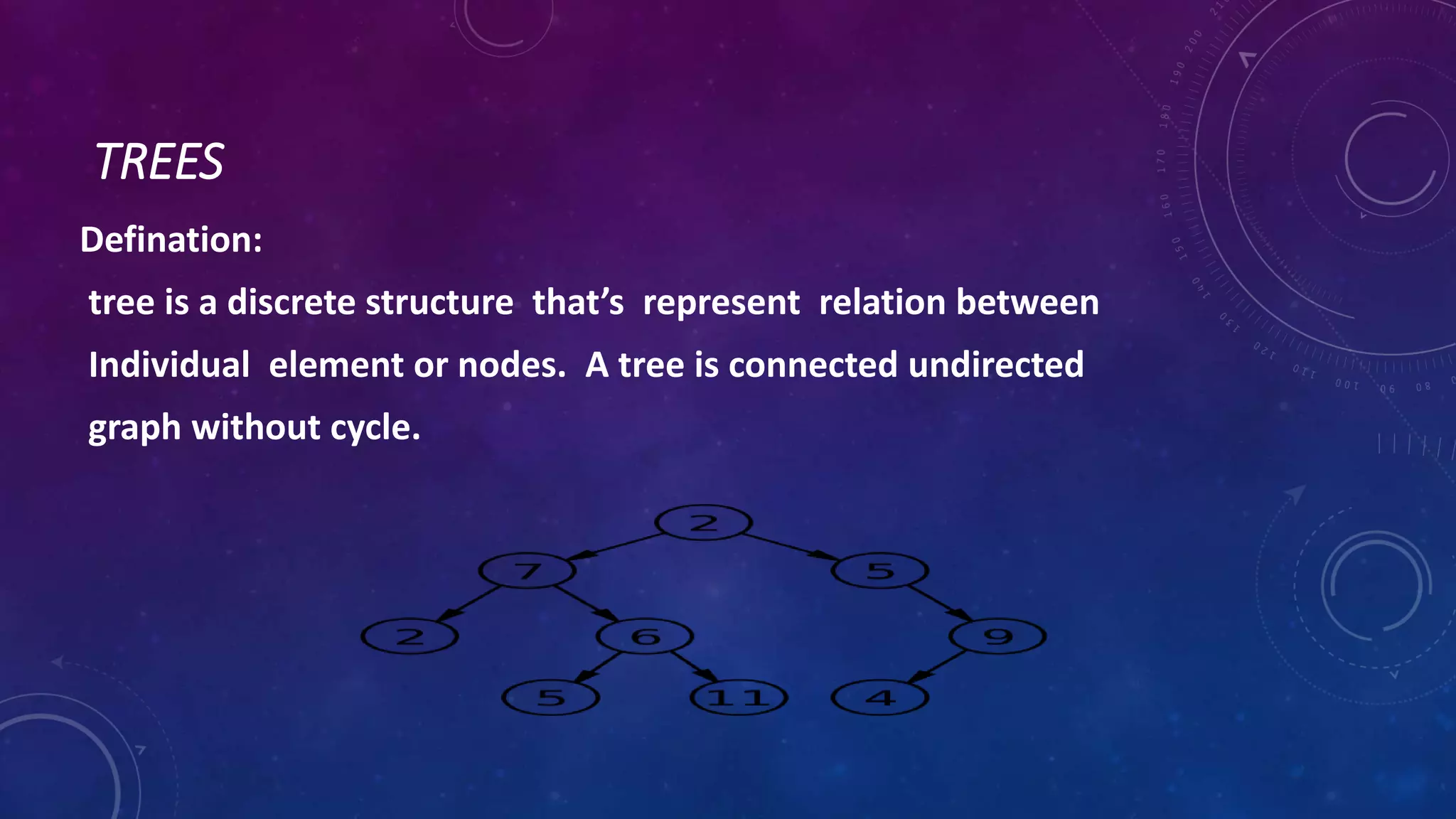
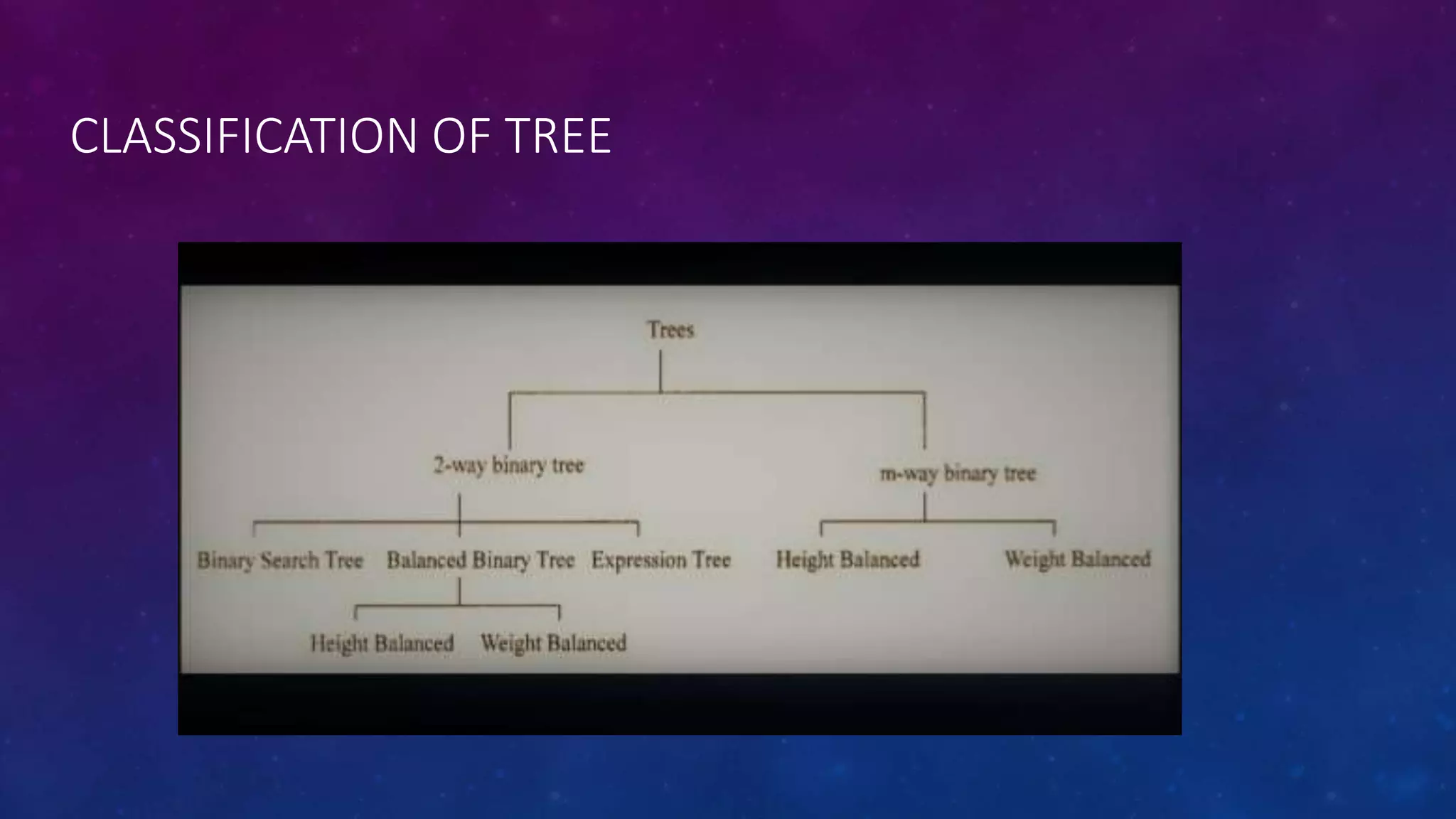
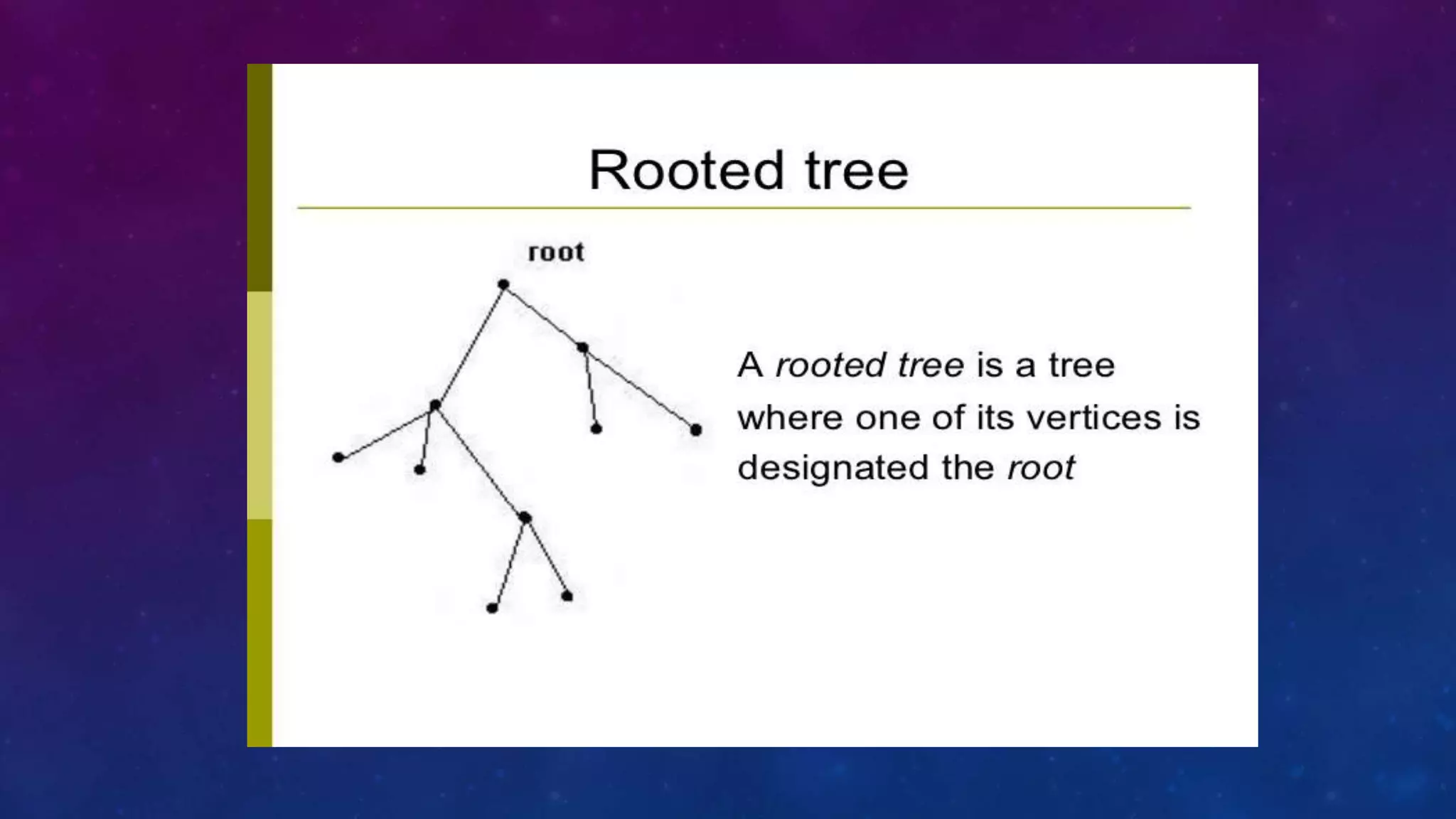
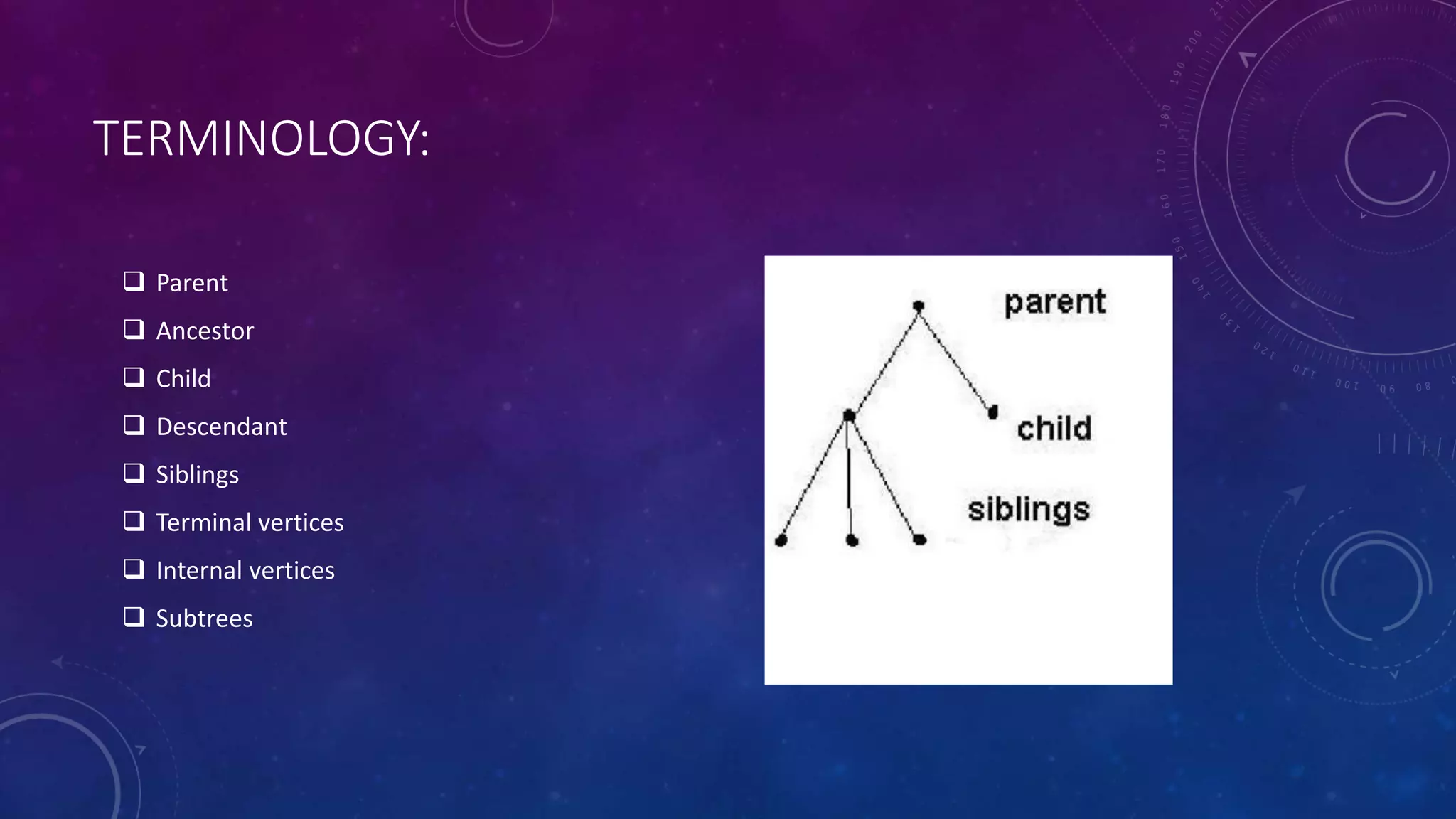
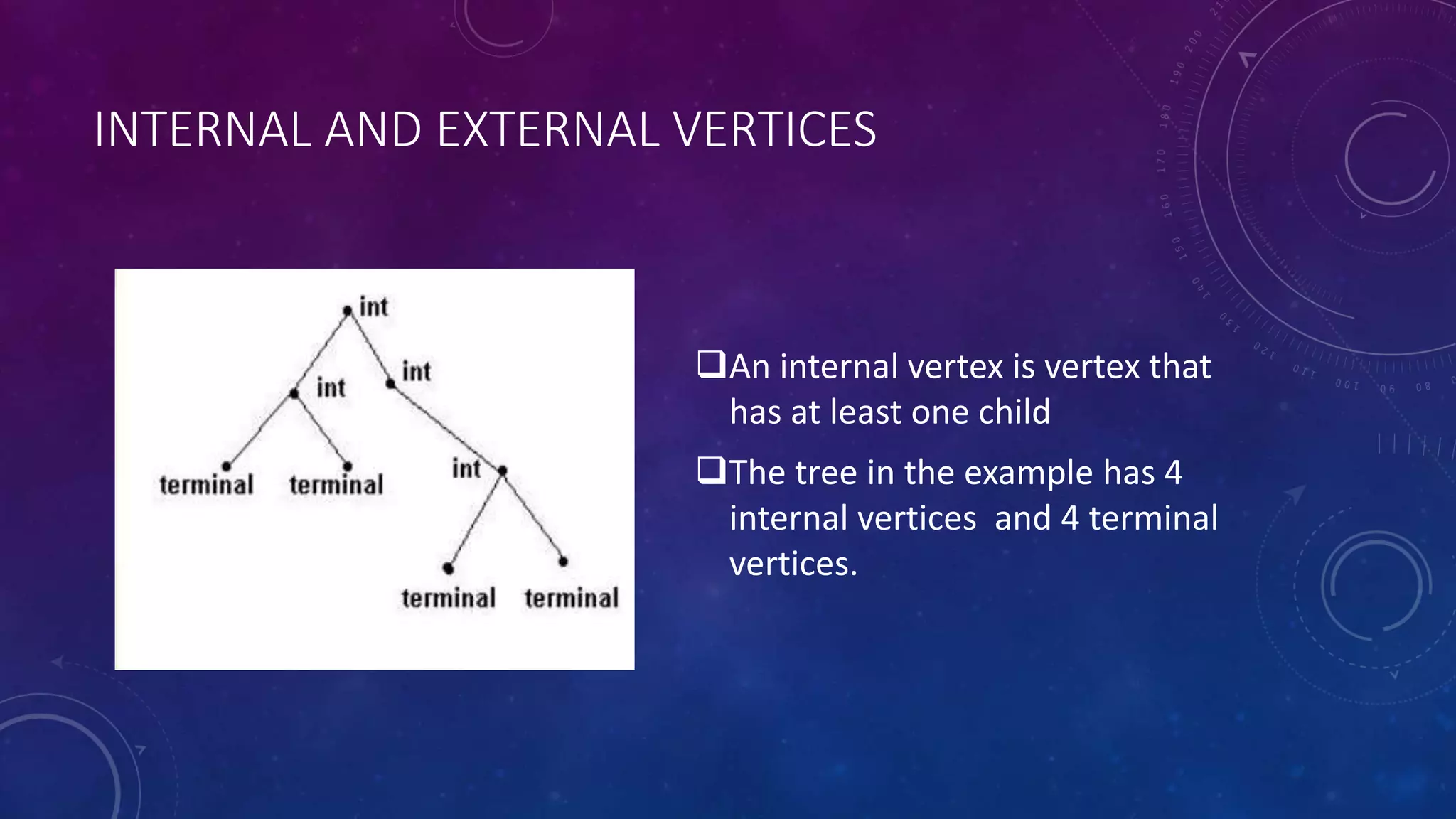
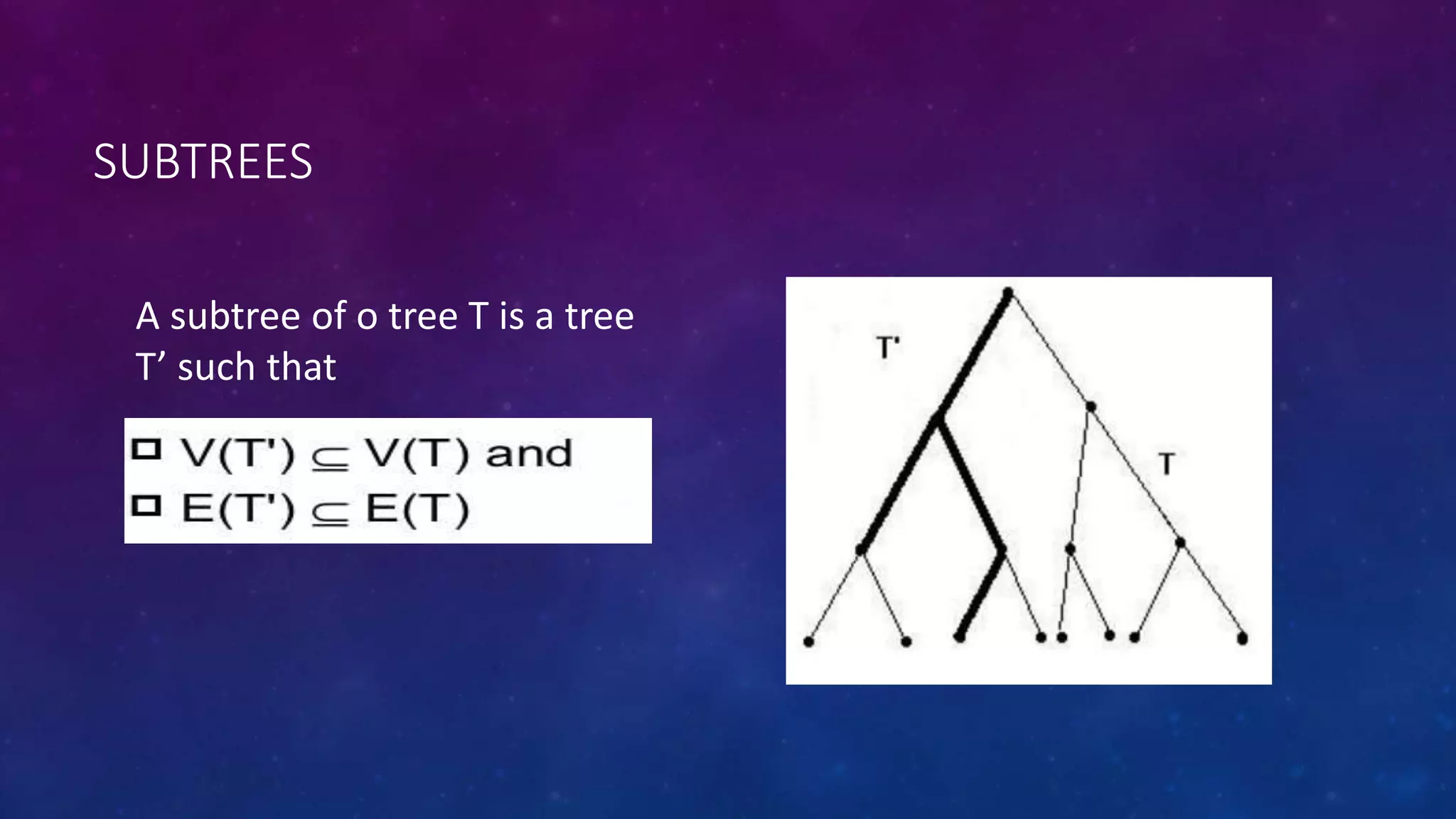
The document discusses different types of trees in discrete mathematics. It defines what a tree is, how trees are represented and classified. It discusses key tree terminology like parent, child, internal/external vertices. It also covers subtrees, spanning trees, minimum spanning trees, and algorithms to find spanning trees. Finally, it discusses binary tree isomorphism testing whether two binary trees are structurally identical by comparing properties like number of vertices and edges and position of children.

1. PRESENTATION
ON
DISCRETE
MATHEMATICS

2. OUR TOPIC:
Different
types
of
Trees

3. GROUP:2
Name Id
Md Tawhidul Islam 171-15-9191
Md Jakiul Rashid Khan 171-15-8554
Asma Sadia Akhi 171-15-8757
Nusrat Jahan eva 171-15-8937
Md Alamin Shah 171-15-8823
Shuvo Podder 171-15-888

4. TREES
Defination:
tree is a discrete structure that’s represent relation between
Individual element or nodes. A tree is connected undirected
graph without cycle.

5. TREE REPRESENTATION
Trees are structures used to represent hierarchical
relationship.
Each tree consists of nodes and edges.
 - each nodes represents a object.
 -each edges represents the relationship between two
nodes.

6. EXAMPLE

7. CLASSIFICATION OF TREE

9. TERMINOLOGY:
 Parent
 Ancestor
 Child
 Descendant
 Siblings
 Terminal vertices
 Internal vertices
 Subtrees

10. INTERNAL AND EXTERNAL VERTICES
An internal vertex is vertex that
has at least one child
The tree in the example has 4
internal vertices and 4 terminal
vertices.

11. SUBTREES
A subtree of o tree T is a tree
T’ such that

12. SPANNING TREES
Given a graph G, a tree T is a s a
spanning tree of G if :
T is a subgraph of G and
T contains all the vertices of G

13. SPANNING TREE SEARCH
 Breadth-first search method
 Depth-first search
method(backtracking)

14. MINIMAL SPANNING TREES
Given a weighted graph G, a
minimum spanning tree is
A spanning tree of G
That has minimum “weight”

15. HEIGHT AND TERMINAL VERTICES
*Theorem7.5.6: If a binary tree
of height ‘h’ has ‘t’ terminal
vertices,thenene lg t<=h,
where lg is logarithm base 2.
Equivalently: t<=2^h.
#Example :h=4 and t=7.
Then t=7<16=2^4=2^h

16. A CASE OF EQUALITY
• #if all ‘t’ teminal vertices of a full binary tree T
have the same lavel
• h=heright of T,then “ t =2^h”.
• Example :
• The height is h=3.
• And the number of terminal vertices is “ t=8.
• } t=8=2^3=2^h..

17. ALPHABETICAL ORDER
Alphabetical or lexicographic order is the order of the
dictionary
a) Start with an ordered set of symbols x={a,b,c,………}…x
can be infinite or finite .
b) Let a=x1,x2,………xm and B=y1,y2……ym
Be strings over X. Then difne a<B if x1<y1.

18. EXAMPLE OF ALPHABIETICAL
ORDER
#Let y=set of letters of the alphabet ordered according to precedence,
I.e.
a<b<c………<x<y<z
*Let a=arborcal. And B=arbiter
• #In this case
• x1=y1=a,
• X2=y2=r,
• X3=y3=b,
So, we get the fourth letter : x4=0 and y4=I,

19. BINARY TREE ISOMORPHISM
Example : The following are two tree.
• Isomorphism are rooted tree.
• Not Isomorphism are binary tree.

20. BINARY TREE ISOMORPHISM
Example : The following are two tree.
Isomorphism are rooted tree.
Not Isomorphism are binary tree.

21. SUMMARY OF TREE ISOMORPHISM
Isomorphism of tree.
Isomorphism of rooted trees.
Isomorphism of binary trees.
(left children goes to left
children,right child goes to
right children)

22. NON ISOMORPHISM OF TREES
Many time it may be easier to determine when two
tree are not isomorphism rather then to show their
isomorphism.
A tree isomorphism must respect certain properties ,
such as
-the number of vertices.
-the number of edges.
-roots must go to roots.
-position of children ,etc.

23. NON ISOMORPHISM OF ROOTED TREES
There are four non isomorphism rooted trees with
four vertices.
The root is the top vertex in each tree.
The degrees of the vertices apper in parenthesis.

24. NON ISOMORPHISM BINARY TREE
There are C(2n,n)/(n+1) non isomorphism binary
trees with n vertices .
C(2n,n)/(n+1) are the Catalan numbers Cn.

25. ISOMORPHISM OF BINARY TREES
There is an algorithm to test whether two binary trees are
isomorphism or not.
If the number of vertices in the two trees is n,
If the number of comparitions needed is an,it can be shown
that an<=3n+2.