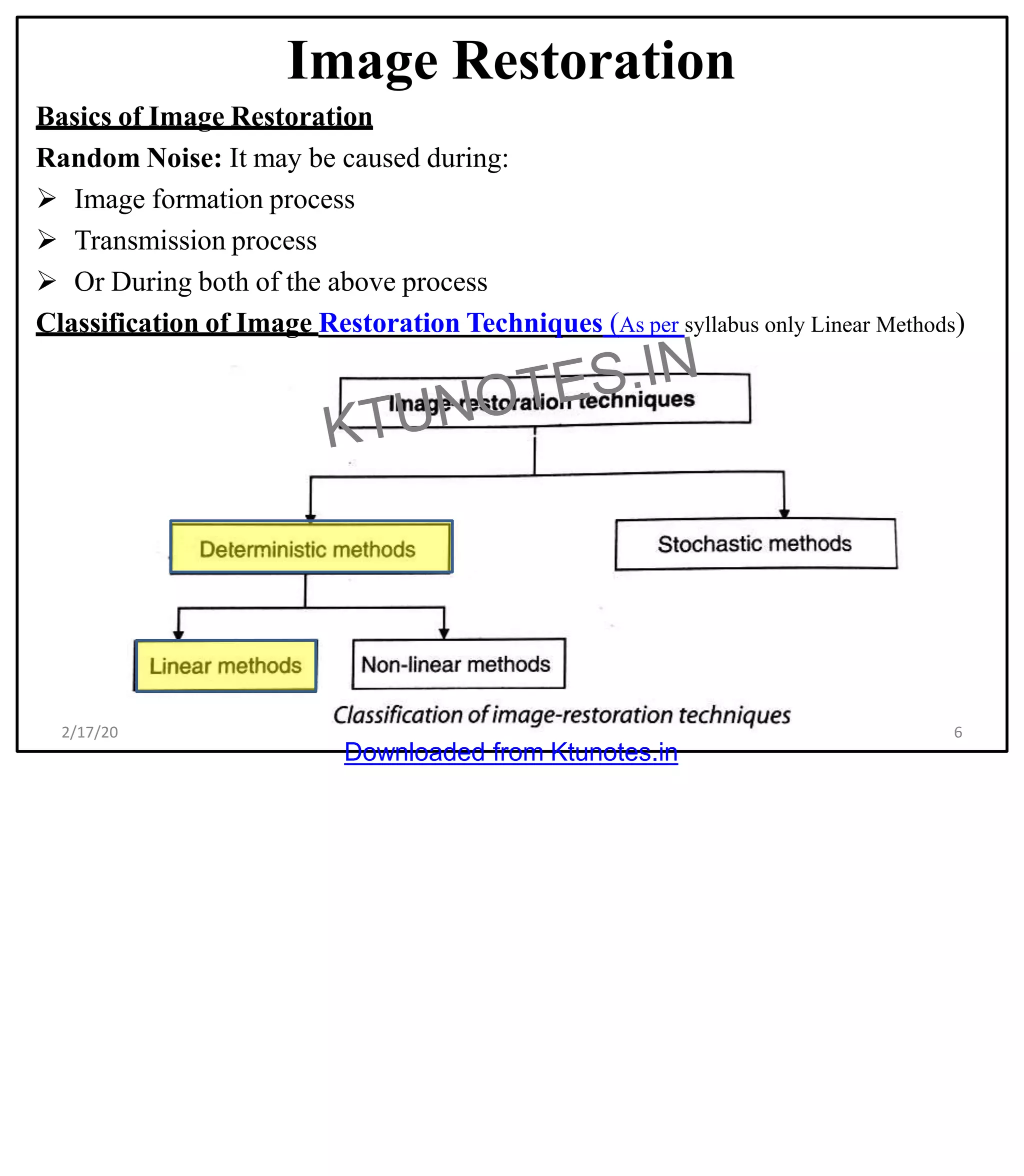
The document discusses image restoration techniques. It defines image restoration as reconstructing an original image from a degraded observation. Image degradation can occur due to deterministic blur from factors like motion blur or random noise during image formation or transmission. Linear image restoration methods include inverse filtering, pseudo-inverse filtering, and Wiener filtering, which aims to minimize mean square error. Geometric transformations can also be used to restore images degraded by changes in geometry through operations like translation, rotation, and scaling.

2. Digital Image Processing
MODULE 4
By
Shyno K G
(Asst. Professor, Dept. Of ECE)
Eranad Knowledge City College of Engineering, Manjeri
Downloaded from Ktunotes.in

3. Image Restoration
Basics of Image Restoration
“ It is the process of reconstructing a version of original image from a degraded
observation”
 Degradation = Deterministic blur + Random noise
 Degradation may happens due to:
Deterministic blur:
 It can be modeled using a mathematical function
 E.g.:
MOD 4
Downloaded from Ktunotes.in
2/17/2018 2

4. Image Restoration
Basics of Image Restoration
Deterministic blur:
= Relative velocity of camera and scene; = angle of motion in readians
2/17/2018 3

5. Image Restoration
Basics of Image Restoration
Deterministic blur:
Motion Blur:
MOD 4
Downloaded from Ktunotes.in
2/17/2018 4

6. Image Restoration
Basics of Image Restoration
Deterministic blur:
MOD 4
Downloaded from Ktunotes.in
2/17/2018 5

7. Image Restoration
Basics of Image Restoration
Random Noise: It may be caused during:
 Image formation process
 Transmission process
 Or During both of the above process
Classification of Image Restoration Techniques (As per syllabus only Linear Methods)
2/17/20 6
18 MOD 4
Downloaded from Ktunotes.in

8. Image Restoration
Image Restoration Model (Degradation model)
 is the Original image
 H is the Degradation function



is the Additive Noise
is the Degraded image
is the Restored image
 Restoration error should be minimized
 With the limited knowledge about H and we estimate a good
approximation for
MOD 4
Downloaded from Ktunotes.in
2/17/2018 7

9. Image Restoration
Image Restoration Model (Degradation model)
 The Degraded image is represented as:
 In frequency domain;
 In Optics, is called OTF(Optical Transfer Function) or it is called the
Point Spread Function
MOD 4
Downloaded from Ktunotes.in
2/17/2018 8

10. Image Restoration
Image Restoration Methods (Deterministic-Linear)
 Deterministic methods use a degradation model having degradation function H
 Within that the linear methods uses a linear restoration model
 Deterministic-Linear image restoration is classified into:
1. Un-constrained restoration
a) Inverse filter
b) Pseudo-Inverse filter
2. Constrained restoration using Lagrange multiplier -
MOD 4
Downloaded from Ktunotes.in
2/17/2018 9

11. Image Restoration
Image Restoration Methods (Deterministic-Linear)
1. Un-constrained restoration
a) Inverse filter
 Here we know the exact Point Spread Function h(m,n)
 We neglect the random noise
 By degradation model:
 For simplicity
 The noise is given by
 For neglecting the noise we need to find an
(1)
(2)
minimize the noise function:
(3)
 The operation is such that we are not giving any constraints for during
minimization, hence the name Un constrained restoration
(4)
MOD 4
Downloaded from Ktunotes.in
2/17/2018 10

12. Image Restoration
Image Restoration Methods (Deterministic-Linear)
1. Un-constrained restoration
a) Inverse filter
 Take the partial derivative of and equate to zero and solve for
(5)
(6)
 Taking Fourier transform on eqn: 6
(7)
 Taking Inverse Fourier transform on eqn: 7
MOD 4
Downloaded from Ktunotes.in
2/17/2018 11

13. Image Restoration
Image Restoration Methods (Deterministic-Linear)
1. Un-constrained restoration
a) Inverse filter-Disadvantages
 Not possible to obtain the inverse
 To exist the inverse the H matrix should be non-singular
 Noise will degrade the performance of inverse filter
 It has tendency to amplify the noise
MOD 4
Downloaded from Ktunotes.in
2/17/2018 12

14. Image Restoration
Image Restoration Methods (Deterministic-Linear)
1. Un-constrained restoration
b) Pseudo Inverse filter
 When the H matrix is non invertible we go for the Pseudo inverse filter
 We know that the inverse filter is given as:
 Where
 i.e.
(1)
represents the point spread function and it is mostly an LPF
Tends to zero at higher frequencies so that the inverse filtering
becomes a multiplication with infinity (Denominator of eqn (1) becomes zero)
 Then the noises get amplified vigorously
 To avoid this we use the Pseudo-inverse filtering given as:
 Proper selection of will give good restoration
MOD 4
Downloaded from Ktunotes.in
2/17/2018 13

15. Image Restoration
Image Restoration Methods (Deterministic-Linear)
1. Un-constrained restoration
b) Pseudo Inverse filter
14
MOD 4
2/17/2018
Downloaded from Ktunotes.in

16. Image Restoration
Image Restoration Methods (Deterministic-Linear)
2. Constrained restoration with Lagrange multiplier
(Constrained Least Square Filter)
 The lost information in the degraded image can be mitigated by constraining
the restoration
 Constraints add information to the process
 Constraints can have additional information about the original scene
 So that the restoration become more faithful
“Constrained restoration is a process of obtaining a meaningful restoration by
biasing the solution towards the minimiser of some specified constraint
function”
 Constrained Least Square Filter is a regularization technique which adds the
Lagrange multiplier to control the balance between noise artifacts and
consistency with the observed data
MOD 4
Downloaded from Ktunotes.in
2/17/2018 15

17. Image Restoration
Image Restoration Methods (Deterministic-Linear)
2. Constrained restoration with Lagrange multiplier
(Constrained Least Square Filter)
 Constrained Least Square Filter is given as:
 Where is the Laplacian filter and has larger amplitudes at high
frequencies where the noise will dominates
 Which reduces noise at high frequencies
 Proper choice of and will reduce noise by minimizing higher order
derivatives
MOD 4
Downloaded from Ktunotes.in
2/17/2018 16

18. Image Restoration
Minimum Mean Square Error (MMSE) Filtering (Wiener Filter)
 Inverse filter has two main drawbacks:
1. At higher frequencies the noises start dominating
2. It assumes the noise to be minimum
 To counteract these problems we use Wiener filter. Which includes both
degradation function H and statistical characteristics of noise
 Introduced by N Wiener in 1942
 The objective is to minimize the MSE :
 Where E{.} is the expectation or mean
 Assumptions:
1. Image and noise are uncorrelated (one or other has zero mean)
2. Intensity levels in the estimated image are a linear function of intensities in
degraded image g
MOD 4
Downloaded from Ktunotes.in
2/17/2018 17

19. Image Restoration
Minimum Mean Square Error (MMSE) Filtering (Wiener Filter)
 In frequency domain Wiener filter/MMSE filter/LSE (Least Square Error)
filter can be given as:
 Where
MOD 4
Downloaded from Ktunotes.in
2/17/2018 18

20. Image Restoration
Minimum Mean Square Error (MMSE) Filtering (Wiener Filter)
 In frequency domain the Signal to Noise Ratio is given by:
(1)
 In Spatial domain Signal power will be
 And Noise power is given as (MSE will be the Noise power)
MOD 4
Downloaded from Ktunotes.in
2/17/2018 19

21. Image Restoration
Minimum Mean Square Error (MMSE) Filtering (Wiener Filter)
 Now, In Spatial domain the Signal to Noise Ratio is given by:
become a constant. Then
 When the noise is WGN then the spectrum
Wiener filter can be given as:
 From eqn (1) the SNR is improved when noise variance is decreased
 Low noise variances can yield excellent results
MOD 4
Downloaded from Ktunotes.in
2/17/2018 20

22. Image Restoration
Minimum Mean Square Error (MMSE) Filtering (Wiener Filter)
Features:
1. Excellent noise removal at all frequencies
2. With lower orders of noise variances the estimate will be very close to original
3. Since it is an unconstraint one it simple
(Problems-Refer Note book)*
DegM
rO
aD
d4
ed
Original Wiener Filtered
2/17/2018 21
Downloaded from Ktunotes.in

23. Image Restoration
Geometric Transformations-Spatial Transformations
 Used when the degradation affects the geometry of an image. E.g. Angle, width
, length or volume etc.
MOD 4
Downloaded from Ktunotes.in
2/17/2018 22

24. Image Restoration
Geometric Transformations-Spatial Transformations
MOD 4
2/17/2018 23
Downloaded from Ktunotes.in

25. Image Restoration
Geometric Transformations-Spatial Transformations
MOD 4
2/17/2018 24
Downloaded from Ktunotes.in

26. Image Restoration
Geometric Transformations-Spatial Transformations
MOD 4
Downloaded from Ktunotes.in
2/17/2018 25

27. Image Restoration
Geometric Transformations-Spatial Transformations
MOD 4
Downloaded from Ktunotes.in
2/17/2018 26

28. Image Restoration
Geometric Transformations-Spatial Transformations
MOD 4
Downloaded from Ktunotes.in
2/17/2018 27

29. Image Restoration
Geometric Transformations-Spatial Transformations
 Rotation & Scaling
2/17/2018 28
MOD 4
Downloaded from Ktunotes.in

30. Image Restoration
Geometric Transformations-Spatial Transformations
MOD 4
Downloaded from Ktunotes.in
2/17/2018 29

31. Image Restoration
Geometric Transformations-Spatial Transformations
MOD 4
Downloaded from Ktunotes.in
2/17/2018 30

32. Image Restoration
Geometric Transformations-Spatial Transformations
MOD 4
Downloaded from Ktunotes.in
2/17/2018 31

33. Image Restoration
Geometric Transformations-Spatial Transformations
MOD 4
Downloaded from Ktunotes.in
2/17/2018 32

34. Image Restoration
Geometric Transformations-Spatial Transformations
MOD 4
Downloaded from Ktunotes.in
2/17/2018 33

35. Image Restoration
Geometric Transformations-Spatial Transformations
MOD 4
Downloaded from Ktunotes.in
2/17/2018 34

36. Image Restoration
Geometric Transformations-Spatial Transformations
2/17/201
8
35
MOD 4
Downloaded from Ktunotes.in

37. Image Restoration
Geometric Transformations-Spatial Transformations
MOD 4
Downloaded from Ktunotes.in
2/17/2018 36

38. Image Restoration
Geometric Transformations-Spatial Transformations
MOD 4
Downloaded from Ktunotes.in
2/17/2018 37

39. Image Restoration
Geometric Transformations-Spatial Transformations
2/17/2018 38
MOD 4
Downloaded from Ktunotes.in

40. Image Restoration
Geometric Transformations-Spatial Transformations
MOD 4
Downloaded from Ktunotes.in
2/17/2018 39

41. Image Restoration
Geometric Transformations-Spatial Transformations
MOD 4
Downloaded from Ktunotes.in
2/17/2018 40

42. Image Restoration
Geometric Transformations-Spatial Transformations
MOD 4
Downloaded from Ktunotes.in
2/17/2018 41

43. Image Restoration
Geometric Transformations-Spatial Transformations
MOD 4
Downloaded from Ktunotes.in
2/17/2018 42