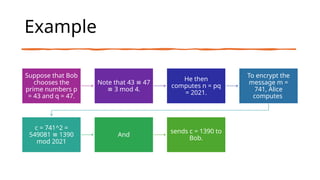
Rabin's public-key cryptosystem, developed in 1979, is based on the difficulty of computing square roots modulo a composite integer n and is secure against chosen-plaintext attacks if factoring large integers is hard. The system involves key generation with two distinct prime numbers, encryption by squaring messages, and decryption which may yield up to four possible plaintexts due to the nature of quadratic congruences. Despite its high security level, the ambiguity in decryption presents challenges for certain applications.

1. Rabin’s Public-Key Cryptosystem

2. Rabin’s Public-Key Cryptosystem
In 1979, Michael O. Rabin
developed a public-key
cryptosystem whose security is
based on the difficulty of
computing square roots
modulo some integer n.
His cryptosystem is provably
secure against chosen-plaintext
attacks, assuming that the
factoring problem is
computationally intractable,i.e.,
assuming that it is hard to find
the prime factors of n = pq by a
randomized algorithm with
nonnegligible probability.

3. Rabin’s Public-
Key
Cryptosystem:
Key Generation.
Bob randomly chooses two
large distinct prime numbers
p and q, which satisfy p q
≡ ≡
3 mod 4.
The pair (p, q) is his private
key.
He then computes n = pq, his
public key.

4. Communication
Bob’s public key n is now known to Alice.

5. Encryption
Given the public key n, Alice computes her ciphertext c by
squaring her message m modulo n, i.e., the encryption
function defined by
Alice sends the ciphertext c to Bob

6. Example
Suppose that Bob
chooses the
prime numbers p
= 43 and q = 47.
Note that 43 47
≡
3 mod 4.
≡
He then
computes n = pq
= 2021.
To encrypt the
message m =
741, Alice
computes
c = 741^2 =
549081 1390
≡
mod 2021
And
sends c = 1390 to
Bob.

7. Decryption:
• Rabin cryptosystem offers a
high level of security, but it
comes with the challenge of
multiple possible decryptions.
• Decryption involves solving a
quadratic congruence, which
can be computationally
expensive.
• The security of Rabin
cryptosystem relies on the
difficulty of factoring large
composite numbers.

8. Decryptio
n:
1.Compute the four possible square roots:
To decrypt, one needs to find the square
roots of c modulo n.
This involves solving the equation x^2 c
≡
(mod n).
There can be up to four possible solutions for
the equations:
x^2 c (mod p)
≡ .
x^2 c (mod q)
≡ .
2. Test the solutions: The correct plaintext
message is the one among the four solutions
that is a valid integer.

9. The four solutions
To solve the equation x^2 c (mod n)
≡ .
The possible solutions must come from the equations:
x^2 c (mod p)
≡ .
x^2 c (mod q)
≡ .
• To solve these, the simplified form is given as:
•
• And
•

10. Solution using CRT
• The equations can thus be written as:
• ;
• ;
• ;
• ;
And thus solved using CRT to give the 4 possible solutions

11. Example:
• Given the prime numbers p = 7 and q = 11, create a Rabin
cryptosystem. Encrypt the message m = 5. Decrypt the
ciphertext and verify
• Encryption:
• Ciphertext: c = m^2 mod n = 5^2 mod 77 = 25 mod 77 = 25.
• Decryption:
• Solve the equation x^2 25 (mod 77)
≡ .

12. Since 77 = 7 * 11, solve the congruence modulo 7 and modulo
11 separately, and then combine the solutions using CRT.
• Solving modulo 7:
• x^2 25 (mod 7)
≡
• x^2 4 (mod 7) thus, x 4^(7+1)/4 (mod 11)
≡ ≡
• x ± 16(mod 7)
≡
• The solutions are x ± 2 (mod 7).
≡
• Solving modulo 11:
• x^2 25 (mod 11)
≡
• x^2 3 (mod 11) thus, x 3^(11+1)/4 (mod 11)
≡ ≡
• x ± 27(mod 11)
≡
• The solutions are x ± 5 (mod 11).
≡

13. • Combining Solutions using CRT: We have the following systems of
congruences:
• x 2 (mod 7)
≡
• x 5 (mod 11)
≡
• x 2 (mod 7)
≡
• x -5 (mod 11)
≡
• x -2 (mod 7)
≡
• x 5 (mod 11)
≡
• x -2 (mod 7)
≡
• x -5 (mod 11)
≡

14. Revisit CRT

15. Using CRT
• x 2 (mod 7)
≡
• x 5 (mod 11)
≡
• Sol 16
• x 2 (mod 7)
≡
• x -5 (mod 11)
≡
• Sol. 72
• x -2 (mod 7)
≡
• x 5 (mod 11)
≡
• Sol 5
• x -2 (mod 7)
≡
• x -5 (mod 11)
≡
• Sol. 61

16. Example:
• Given the prime numbers p = 7 and q = 11, create a Rabin cryptosystem.
Encrypt the message m = 10. Decrypt the ciphertext and verify
• Encryption:
• Ciphertext: c = m^2 mod n = 10^2 mod 77 = 23.
• Decryption:
• Solve the equation x^2 23 (mod 77)
≡ .
• Solutions: x = 10, 67, 32, 45

17. Security of the Rabin Cryptosystem
The security of the Rabin cryptosystem relies on the difficulty of
factoring large numbers.
If an attacker can factor the modulus n, they can easily decrypt any
ciphertext.
However, the Rabin cryptosystem has a significant drawback:
Ambiguity in decryption:
For any ciphertext, there are four possible plaintext values. This
ambiguity can make it difficult to use Rabin for certain applications.