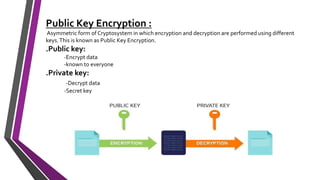
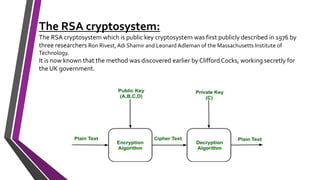
The document covers number theory, including concepts like divisibility, greatest common divisor, and prime numbers, highlighting its application in cryptography. It details encryption methods, such as Caesar and shift ciphers, alongside public and private key cryptosystems like RSA. Additionally, it discusses cryptographic protocols for key exchange and the importance of digital signatures for authentication and integrity.

1. Presentation
CourseTitle: Discrete Structures
Course Code: CS-261
Presented to: Ma’am Ayesha Rashid
Presented by:
Maliha Shafi (23021519-029)
Maida (23021519-067)
Samreen (23021519-077)
Anam Asjad (23021519-105)
Kinza Karam (23021519-178)
Class: BS-CS (C)
Department: Computer Science

2. Number theory

3. 3
Number theory is a branch of pure mathematics
devoted primarily to the study of the integers and
integer-valued functions. It is concerned with
properties and relationships of numbers, especially
the properties of the integers, or whole numbers.
Number theory is often referred to as "higher
arithmetic" because it involves the study of numbers
beyond basic arithmetic operations.

4.  THE BASIC PRINCIPLE
OF :
DIVISION

5. IF A AND B ARE INTEGERS WITH A  0, WE SAY
THAT
A DIVIDES B IF THERE IS AN INTEGER C SO THAT
B = AC.
WHEN A DIVIDES B WE SAY THAT A IS A FACTOR
OF B AND THAT B IS A MULTIPLE OF A.
THE NOTATION A | B MEANS THAT A DIVIDES B.
WE WRITE A X B WHEN A DOES NOT DIVIDE B

6. DIVISIBILITY
THEOREM
6

7. 7
For integers a, b, and c it is true that
• if a | b and a | c, then a | (b + c)
Example: 3 | 6 and 3 | 9, so 3 | 15.
• if a | b, then a | b.c for all integers c
Example: 5 | 10, so 5 | 20, 5 | 30, 5 | 40, …
• if a | b and b | c, then a | c
Example: 4 | 8 and 8 | 24, so 4 | 24.

8. DIVISION
ALGORITHM
8

9. 9
Let a be an integer and d a positive integer.
Then there are unique integers q and r, with
0  r < d, such that a = dq + r.
In the above equation,
• d is called the divisor,
• a is called the dividend,
• q is called the quotient, and
• r is called the remainder.

10. Example:
When we divide 17 by 5, we have
17 = 5.3 + 2.
17 is the dividend,
5 is the divisor,
3 is called the quotient, and
2 is called the remainder.
10

11. Another example:
What happens when we divide -11 by 3 ?
Note that the remainder cannot be negative.
-11 = 3(-4) + 1.
-11 is the dividend,
3 is the divisor,
-4 is called the quotient, and
1 is called the remainder.
11

22. Greatest Common Divisor (GCD)
 GCD of two or more integers is the largest positive integer that divides each of the
integers.
 "A positive integer c is called greatest common divisor of a and b if c divides both a and b”.
It is denoted: gcd(a, b)
 The greatest common divisor of two positive integers can be found by using their prime
factorizations.
 We say that two integers are relatively prime if their greatest common division (gcd) is 1.7

24. Primes
 Definition:
A positive integer p greater than 1 is called prime if the only positive factors of p are 1
and p . A positive integer that is greater than 1 and is not prime is called composite.
 Example:
The integer 7 is prime because its only positive factors are 1 and 7, but 9 is composite
because it is divisible by 3.

25. CRYPTOGRAPHY
Introduction:
• Cryptography is the science of securing
communication by transforming information into a
format that prevents unauthorized access. It involves
encryption (encoding) and decryption (decoding)
processes.
• Number theory plays a key role in cryptography

26. Basic Concepts:
Encryption and Decryption:
Encryption: Converting plaintext into cipher text using an algorithm and a key.
Decryption:Converting cipher text back to plaintext using a key.
Keys:
• Symmetric Key Cryptography: Same key for encryption and
decryption.
• Asymmetric Key Cryptography: Different keys for encryption (public
key) and decryption (private key).

27. Classical Cryptography:
Caesar Cipher:
 One of the earliest known uses of cryptography was by Julius Caesar.
 He made messages secret by shifting each letter three letters forward in the
alphabet.
For example: A → D, B → E, C → F, ..., X →A,Y → B, Z → C.
 To express Caesar’s encryption process mathematically, first replace each
letter by an element of Z26, that is, an integer from 0 to 25 equal to one less
than its position in the alphabet.
For example:

28. • Caesar’s encryption method can be represented by the function f that assigns to the
nonnegative integer p, p ≤ 25, the integer f (p) in the set {0, 1, 2,..., 25} with
f (p) = (p + 3) mod 26
EXAMPLE :What is the secret message produced from the message “MEETYOU INTHE
PARK” using the Caesar cipher?
Solution: First replace the letters in the message with numbers.
This produces 12 4 4 19 24 14 20 8 13 19 7 4 15 0 17 10.
Now replace each of these numbers p by f (p) = (p + 3) mod 26.
This gives 15 7 7 22 1 17 23 11 16 22 10 7 18 3 20 13.
Translating this back to letters produces the encrypted message “PHHW BRX LQ WKH
SDUN.”
 To recover the original message from a secret message encrypted by the Caesar cipher
(Decryption):
f −1(p) = (p − 3) mod 26

29. Shift cipher:
 Instead of shifting the numerical equivalent of each letter by 3, we can shift the
numerical equivalent of each letter by k, so that
f (p) = (p + k) mod 26.
Such a cipher is called a shift cipher. Note that decryption can be carried out using
f −1(p) = (p − k) mod 26.
Here the integer k is called a key.
 For Example:We agree with our friend to use the Shift Cipher with key K=19 for
our message.
We encrypt the message "KHAN", as follows:

30. So, after applying the Shift Cipher with key K=19 our message text "KHAN" gave us cipher
text "DATG".
• Our friend now decodes the message
using our agreed upon key K=19. As follows:
So, after decrypting the Shift Cipher with key K=19 our friend deciphers the cipher text
"DATG" into the message text "KHAN".
Pros and Cons of Caeser and Shift Cipher:
Pros:
• Simple and easy to implement.
• Introduces the basic idea of encryption.

31. Cons:
• Very easy to break with brute force (only 25 possible shifts).
• Vulnerable to frequency analysis attacks.
Block Cipher:
 We can make it harder to successfully attack cipher text by replacing blocks of letters
with other blocks of letters instead of replacing individual characters with individual
characters; such ciphers are called block ciphers.
 A simple type of block cipher is called the transposition cipher.
As a key we use a permutation σ of the set {1, 2,...,m} for some positive integer m, that
is, a one-to-one function from {1, 2,...,m} to itself.
To encrypt a message we first split its letters into blocks of size m. (If the number of
letters in the message is not divisible by m we add some random letters at the end to fill
out the final block.)
To decrypt a cipher text block c1c2 ...cm, we transpose its letters using the permutation
σ −1, the inverse of σ

32. EXAMPLE : Using the transposition cipher based on the permutation σ of the set
{1, 2, 3, 4} with σ (1) = 3, σ (2) = 1, σ (3) = 4, and σ (4) = 2, Encrypt the plaintext
message PIRATE ATTACK
We first split the letters of the plaintext into blocks of four letters.We obtain
PIRA TEAT TACK.To encrypt each block, we send the first letter to the third
position, the second letter to the first position, the third letter to the fourth
position, and the fourth letter to the second position. We obtain IAPR ETTA AKTC.
Cryptosystems:
A cryptosystem is a structure or scheme consisting of a set of algorithms that
converts plaintext to cipher text to encode or decode messages securely.
Cryptosystem provides a general structure for defining new families of ciphers.

33.  A cryptosystem is a five-tuple (P, C, K, E, D), where P is the set of plaintext strings, C is
the set of ciphertext strings, K is the keyspace (the set of all possible keys), E is the set of
encryption functions, and D is the set of decryption functions.
We denote by Ek the encryption function in E corresponding to the key k and Dk the
decryption function in D that decrypts ciphertext that was encrypted using Ek, that is
Dk(Ek(p)) = p, for all plaintext strings p.
Cryptanalysis:
 Cryptanalysis is the study of breaking cryptographic systems, deciphering encrypted
messages, and finding weaknesses in security protocols without access to the
decryption key.
 It involves using various methods, such as analyzing patterns, exploiting vulnerabilities,
and employing computational techniques, to decrypt encrypted data and compromise
security measures.

34. • Asymmetric.
• In public key cryptosystem,
knowing how to encrypt a
message does not help one to
decrypt the message.
• Therefore, everyone can have
publicly known encryption key.
• The only key that needs to be
kept secret is the decryption
key.
• Symmetric.
• All classical ciphers including shift
cipher, are private key cryptosystems.
• Knowing the encryption key allows
one to quickly determine the
decryption key.
• All parties who wish to communicate
using a private key must share a key
and keep it a secret.
Private key
cryptosystem:
Public key
cryptosystem:

35. Public Key Encryption :
Asymmetric form of Cryptosystem in which encryption and decryption are performed using different
keys.This is known as Public Key Encryption.
.Public key:
-Encrypt data
-known to everyone
.Private key:
-Decrypt data
-Secret key

36. The RSA cryptosystem:
The RSA cryptosystem which is public key cryptosystem was first publicly described in 1976 by
three researchers Ron Rivest,Adi Shamir and Leonard Adleman of the Massachusetts Institute of
Technology.
It is now known that the method was discovered earlier by Clifford Cocks, working secretly for
the UK government.

37. RSA public and private key:
Formula’s:
->Public key= (e,n)
where
.e=encryption exponent
.n=product of two large prime numbers
->Private key= (d,n)
Where
.d=decryption exponent
. n=product of two large prime numbers

38. Calculations:
• Ch00se two different large prime numbers i.e. p and q.
• Calculate n=p* q
• Calculate Φ(n)=( p-1)*(q-1)
• Choose “e” such that 1<e<(n)
where e is co-prime to Φ(n), gcd (e, (n))= 1
• Calculate d such that de≅ 1 mod (c)
• Public key “e” and private key “d”

39. 1. p=13 ,q=17
2. n=p*q = 13*17 = 221
3. Φ(n) = (p-1)*(q-1) = (13-1)*(17-1) =12*16 =192
4. e= 35 , gcd (35,192)=1
5. de=1+k. Φ(n) , d= 1+k. Φ(n) /e
where k=0,1,2,……
d=1+2.192/35=11
6. Public key= (e,n) =(35,221)
Private key=(d,n)=(11,221)

40. RSA encryption:
Formula:
c = me mod n
RSA decryption:
Formula:
m = cd mod n
Suppose
Message= 19
Encrypt=19^35 mod
221 = X
Decrypt=X^11 mod 221
= 19

41. Example:
P=7,q=11,n=77
Ali chooses e=17, making d=53
Bob wants to send Ali secret message
HELLO(07 04 11 11 14)
-07^17 mod 77= 28
-04^17 mod 77= 16
-11 ^17 mod 77= 44
-11^17 mod 77= 44
-14^17 mod 77= 42
.Bob sends 28 16 44 44 42 which is received by Ali.
Ali uses private key ,d=53 , to decrypt message:
-28^53 mod 77= 07
-16^53 mod 77= 04
-44^53 mod 77= 11
-44^53 mod 77= 11
-42^53 mod 77= 14
.Ali translates 07 04 11 11 14 to HELLO.
No one else could read it, as onlyAli know his private key (decryption key).

42. Cryptographic Protocols: Key
Exchange
1
Diffie-Hellman
Key Exchange
This protocol allows two
parties to establish a
shared secret key over
an insecure channel,
without prior knowledge
of each other.
2 Man-in-the-Middle
Attack
An attacker can
potentially intercept the
key exchange and
impersonate both
parties, known as a
man-in-the-middle
attack.
3 Authentication
To prevent man-in-the-
middle attacks, key
exchange protocols can
be combined with
authentication
mechanisms, such as
digital signatures.

43. Cryptographic Protocols: Digital
Signatures
Authentication
Digital signatures
provide authentication,
ensuring the message
originated from the
claimed sender.
Non-Repudiation
The signer cannot
deny having created
the digital signature,
providing non-
repudiation.
Integrity
Digital signatures also
ensure the integrity of
the message,
preventing
unauthorized
modifications.
Encryption
Digital signatures can
be combined with
encryption to provide
end-to-end secure
communication.

44. THANK YOU