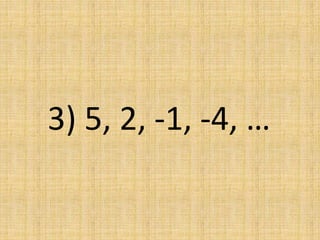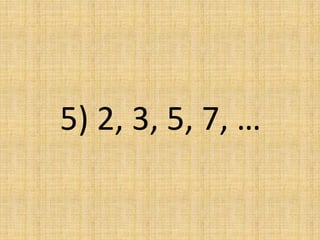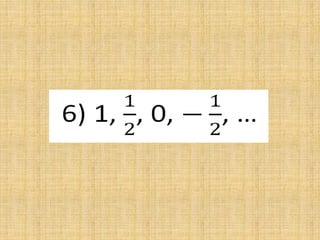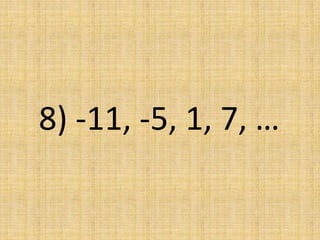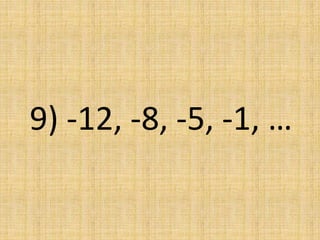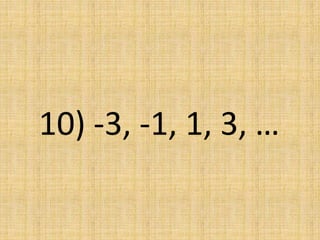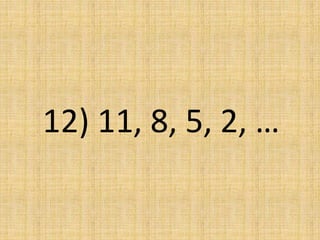Downloaded 30 times
Uploaded bySolomon Hippocrates S. Flores
Definition of Arithmetic Sequence
The document discusses arithmetic sequences, which are sequences where each term is obtained by adding a constant value, called the common difference, to the preceding term. It provides examples of arithmetic sequences and their common differences. It then asks the reader to determine if given sequences are arithmetic, and if so, to find the common difference and identify the next term.
More Related Content
Similar to Definition of Arithmetic Sequence
Definition of Arithmetic Sequence
- 1. ARITHMETIC SEQUENCE Solomon Hippocrates S.Flores E. Rodriguez Vocational High School
- 2. How many wheelsdo you see?
- 3. How about onthis one?
- 4.
- 5. What if 10tricycles pass by, how many wheels would you see? How about 15 tricycles?
- 6. The above situationwill give us the following list: 3, 6, 9, … a10 and 3, 6, 9, … a15. Can we find a way to actually determine the number of wheels of n number of tricycles without actually seeing or counting one?
- 7. Consider the following sequences: 1)4, 5, 6, 7, … 2) - 4, - 7, - 10, - 13, … 3) 1.5, 2.5, 3.5, 4.5, … Find out how the succession of terms is obtained.
- 8. The sequences aboveshow that a constant, either positive or negative, is added to the preceding term to get the next term. Such situation is called an Arithmetic Sequence.
- 9. An arithmetic sequenceis a sequence in which any term is obtained by adding a constant to the preceding term. The number added to any term to get the next term is the difference between two successive terms, hence, the common difference, denoted by d, which can either be positive or negative.
- 10. Determine if thefollowing sequence is arithmetic or not. If yes, find the common difference d and identify the next term. 1) 5, 12, 19, 26, …
- 11. 2) 0.6, 3.1,5.6, 8.1, …
- 12. 3) 5, 2,-1, -4, …
- 14. 5) 2, 3,5, 7, …
- 16. 7) 3, 8,13, 18, …
- 17. 8) -11, -5,1, 7, …
- 18. 9) -12, -8,-5, -1, …
- 19. 10) -3, -1,1, 3, …
- 21. 12) 11, 8,5, 2, …
- 22. 13) 5, 10,15, 20, …
- 23. 14) 0, -3,-6, -9, …
- 24. 15) -80, -1,-78, …
- 25. VALUES INTEGRATIONDiligence can helpbring you to a targeted end.Name a sequence of steps that you can set for yourself when aiming for a target.
- 26. Complete the following statements: 1. Anarithmetic sequence is a sequence in which any term is obtained by ______ a _________ to the ______________ terms. 2. The common difference, d, is the _______ added to _____ term to get the _____ term which can either be __________ or __________.
- 27. Find the commondifference, d, in each of thefollowing sequence. , , 1) -2, 4, 10, … 6) 28.5, 26.3, 24.1, … 2) -21, -15, -9, … 7) 5, -1, -7, … 3) -18, -16, -14, … 8) -16, -12, -8, … 4) 1.5, 3, 4.5, … 9) , , , … 5) 4x, -3x, -10x, … 10) 4.5, 2.1, -0.3, …
- 28. Assignment Determine if thefollowing sequence is arithmetic or not. If yes, find the common difference and identify the next term. 1) -2, 4, 10, … 2) 2, -2, 2, -2, … 3) 4.5, 2.1, -0.3, … 4) 6, 12, 19, 26, … 5) 5, -1, -7, …
- 29.