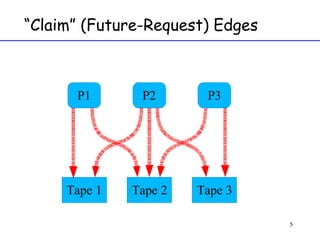
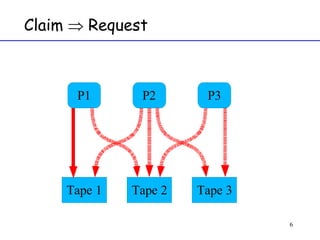
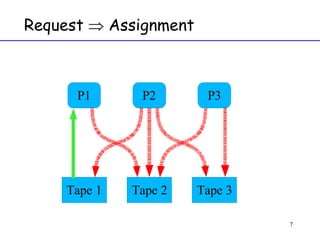
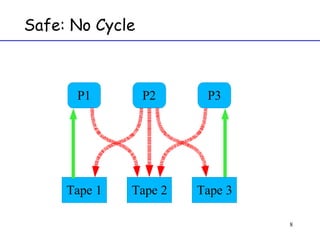
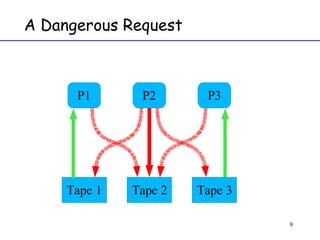
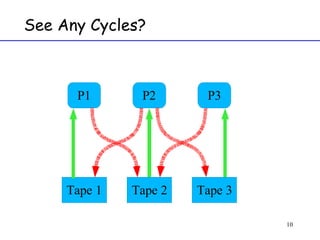
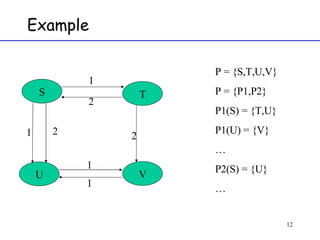
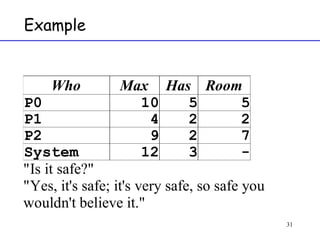
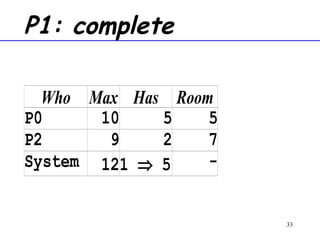
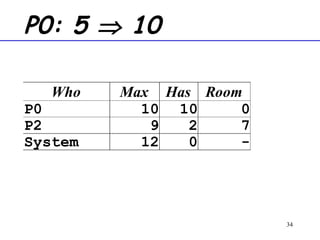
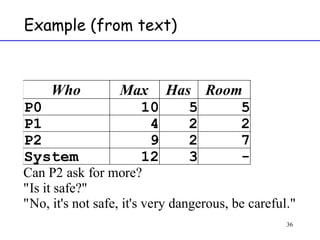
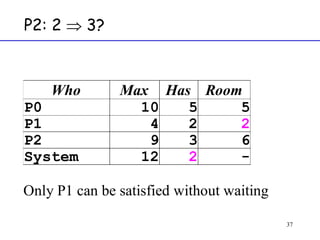
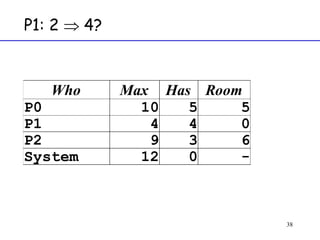
The document discusses deadlock in computer systems. It defines deadlock and lists necessary conditions for deadlock including mutual exclusion, hold and wait, no preemption, and circular wait. It also discusses strategies for dealing with deadlock such as detection, recovery, and prevention/avoidance. The resource allocation graph (RAG) model is introduced as a way to represent system states and detect deadlock. Algorithms like Banker's algorithm aim to avoid deadlock by ensuring safe allocation of resources.

1. Deadlock

2. Deadlock Def. A set of processes is deadlocked if each process in the set is waiting for an event that only another process in the set can cause. Necessary Conditions for Deadlock Mutual Exclusion: Processes claim exclusive control of the resources they require. Hold and Wait: Processes hold resources already allocated to them while waiting for additional resources. No Preemption: Resources cannot be forcibly removed from the process holding them until the resources are used to completion. Circular Wait: A circular chain of processes exists such that each process hold one or more resources that are being requested by the next process in the chain.

3. Dealing with Deadlock Three principle strategies for dealing with deadlock Detection: How can deadlock be identified? Recovery: What are the “best” ways to recover from deadlock? Prevention (and Avoidance): How can deadlock be prevented in the first place? Avoidance: Can we avoid deadlock through careful allocation scheme?

4. Relevant Events A process follows the following sequence to use resources: Request (resource) Use (resource) Release (resource) The three important events are when the process requests , acquires , and releases resources.

5. “ Claim” (Future-Request) Edges

6. Claim  Request

7. Request  Assignment

8. Safe: No Cycle

9. A Dangerous Request

10. See Any Cycles?

11. A System Model A system is a pair ( S , P ) where S is a set of system states {S,T,U,V,...} and P is a set of processes {P 1 ,P 2 ,...} . A process P i is a partial function from system states into nonempty subsets of system states, P i : S  2 S Def. A process P i is blocked in state S if there exists no T such that S  i T . (A process is blocked in a given state if it can't change state.) Def. A process P i is deadlocked in state S if for all T such that S  * T , P i is blocked in T . Ex1. P 2 is blocked (and deadlocked) in both U and V . Ex2. P 1 is blocked but not deadlocked in T . Def. A state S is called a deadlock state if there exists a process P i that is deadlocked in S . Def. A state S is a safe state if for all T such that S  i T , T is not a deadlock state.

12. Example V U T S P = {S,T,U,V} P = {P1,P2} P1(S) = {T,U} P1(U) = {V} … P2(S) = {U} … 1 2 1 2 1 1 2

13. Resource (Allocation) Graph (RAG) A directed graph is a pair (N,E) , where N is a set of nodes and E is a set of ordered pairs (a,b) , a,b  N , called edges. Def. A RAG is a directed graph with N = P  R where P = {P 1 ,...,P n } a set of process nodes and R = {R 1 ,...,R m } a set of resource nodes. The graph is “bipartite” with respect to P and R . An edge (P i ,R j ) is called a request edge (request by P i for 1 unit of R j ). An edge (R j ,P i ) is called an assignment edge (allocation of 1 unit of R j to P i ). For each resource R i  R , there exists a non-negative integer t I denoting the number of units of R i .

14. Invariants on RAG Let |(a,b)| be the number of edges directed for node a to node b . Then   j |(R i ,P j )|  t i for all i . (No more than t i assignments (allocation) may be made for R i .) |(R i ,P j )| + |(P j ,R i )|  t i for all i and j . (The sum of the requests and allocation of any process for a particular resource cannot exceed the available units.)

15. State Transitions The system state is changed to a new state only as a result of requests, releases, or acquisitions of resources by a single process. Request. If a system is in state S and process P i has no requests outstanding (no request edges), then P i may request any # of resources. The system then enters state T , say Release. P i can cause a state change from S to T by a release operation iff P i has no requests and some allocations. P i may release any nonempty subset of its resources in this operation.

16. Acquisition. A system can change from state S to state T by an acquisition operation by iff P i has outstanding requests and all such requests can be satisfied; for all resources R j such that ( P i , R j )  E , we have A process P i is blocked if it is unable to perform any of these operations: 1, 2, or 3. That is, if there exists at least one resource R j such that State Transitions (con’d)

17. Reduction on RAG A RAG is reduced by a process P i , which is neither blocked nor an isolated node, by removing all edges to and from P i . A RAG is irreducible if the graph cannot be reduced by any process. A RAG is completely reducible if there exists a sequence of reductions that deletes all edges of the graph.

18. Theorems Theorem 1: S is a deadlock state iff the RAG of S is not completely reducible. Cor. 1: A process P i is not deadlocked iff a series of reductions leaves a state in which P i is not blocked. Cor. 2: If S is a deadlock state, then at least two processes are deadlocked in S . Theorem 2: A cycle in a RAG is a necessary condition for deadlock. Theorem 3: If S is not a deadlock state and then T is a deadlock state iff the operation by P i is a request and P i is deadlocked in T .

19. Data structures for RAG RAG can be represented by An allocation matrix A, where A ij =| ( P i , R j ) | for i = 1,…,n, j = 1,…,m. A request matrix B, where B ij =| ( P i , R j ) | for i = 1,…,n, j = 1,...,m. will use B i to denote i-th row, i.e., B i = ( B i1 ,..., B im ). An available vector T, where T i = # of available unit for R i , i = 1,...,n.

20. Deadlock Detection Algorithm L := {}; repeat L' := L; for i:=1 to n do if Pi not in L and Bi <= T then T := T + Ai; L := L U {Pi}; end if end for until L = L'; Deadlock := not( L = {Pi, ..., Pn})

21. Example A | R1 R2 R3 B | R1 R2 R3 --------------- --------------- P1 | 1 1 1 P1 | 3 2 1 P2 | 1 1 1 P2 | 2 2 1 P3 | 1 1 1 P3 | 1 1 1 P4 | 1 1 1 P4 | 0 0 0 T = (0, 0, 0). Inspection order P 1 , P 2 , ... Reduction order P n , P n-1 , ... # of process inspections = n + (n-1) + ... = n(n+1)/2 So worst-case exec. time = O(mn 2 )

22. Recovery Recovery through preemption Recovery through rollback Recovery through killing processes

23. Prevention Eliminate possibilities Techniques Serialization (Prevention) One-shot allocation (Prevention) Hierarchical allocation (Prevention) Banker’s algorithm (Avoidance)

24. Serialization Only one process may hold resources at any time. Very inefficient use of resources

25. One-shot Allocation A process may only request all its resources at one time. It is blocked until the entire request can be satisfied. Resources are locked even if they are not in use. This method may be necessary for real-time processes that must be guaranteed not to wait for resource allocation once they are underway. O.w., it is too conservative.

26. Hierarchical Allocation Algorithm: Resources are grouped into levels. A process may only request resources at levels higher than any resource currently held by that process. Resources may be released in any order.

27. Proof that deadlock cannot occur Proof by Induction: Assume N is highest and 0 is lowest. Induction hypothesis: Resources requested at levels  i will always be acquired and released in a finite time. (No circular wait is possible.) Induction basis: The hypothesis is true for i = highest level N. Induction step: Suppose a process has requested resources at level i-1 .. It will be delayed if other processes have those resources. Each of these other processes must release them eventually, or be blocked waiting for resources at level i or higher. By induction hypothesis, this blockage cannot last forever.

28. Properties When all requests are at the same level, this method is equivalent to one-shot allocation. Resources at lower levels are blocked for longer periods, but those at higher levels are shared well. Thus, place the scariest resources at the highest levels so that requests for them will be made only when they are actually needed by a process. This method works well when the resources are semaphores. semaphore S1,S2,S3 P(S1,S2,S3) P(S1) P(S2) P(S2) P(S3) P(S3) P(S1) V(S1,S2,S3) order of V's doesn't matter

29. Avoidance The question is: “Is there an algorithm that can always avoid deadlock by making the right choice all the time?” Deadlock is the result of granting a resource. Banker’s algorithm

30. Banker's Algorithm Each process starts with a claim. A process may never request more than its claim. (However, the sum of the claims of all process may exceed the number of resources.) The current allocation state is kept separately for each resource type: (a) For each process: (1) claim (2) holdings (acquired resources) (3) outstanding request (if process is blocked for allocation) (b) Amount of unallocated resources.

31. Example

32. P1: 2  4

33. P1: complete

34. P0: 5  10

35. P0: complete

36. Example (from text)

37. P2: 2  3?

38. P1: 2  4?

39. P1: complete?

40. Safe state An allocation state is realizable if (a) each claim  maximum available. (b) each process is holding  its claim. (c) the total amount of held resources is  the total available. Otherwise, the allocation state is unrealizable. A realizable state is safe if there is a sequence of processes, P 1 ,...,P n ,(a safe sequence ) such that: P 1 can finish (i.e., there are enough unallocated resources to satisfy its claim.) In general, P i can finish if P i-1 releases its current holding. The state is safe because we can avoid deadlock at the moment by blocking any new processes (or any new claims) until all the current processes have finished in the safe order.

41. Example (One resource class only) process holding max claims A 4 6 B 2 7 C 4 11 unallocated: 2 safe sequence: A,B,C If B should have a claim of 9 instead of 7, there is no safe sequence.

42. Unsafe state An unsafe state is deadlock free if there is a sequence of processes, P 1 ,...,P n , (a deadlock free sequence) such that P 1 might finish. (There are enough unallocated resources to satisfy its current outstanding requests, but not necessarily its entire claim.) In general, P i might finish if P i-1 does. The state is deadlock free since no process is waiting. However, it may be unsafe because the processes may now request resource that put them in a deadlock state, no matter what action the allocator takes.

43. Example process holding max claims outstanding requests A 4 6 2 B 2 9 6 C 4 11 7 unallocated: 2 deadlock-free sequence: A,B,C However, this sequence is not safe: if B should have 7 instead of 6 outstanding requests, deadlock exists.

44. Banker’s algorithm The Banker's Algorithm: satisfy a request iff the resulting state is safe. The Banker's Algorithm is conservative: it cautiously avoids entering an unsafe state even if this unsafe state has no deadlock. It also requires prior claims. deadlock unsafe safe

45. Implementation method Find a safe sequence whenever a request is made. If unsuccessful, block the requester. When a resource is released, consider again allocating resources to blocked processes. The cost of finding a sequence is O(n 2 ) not O(n!) . If more than one resource type, the same sequence must work for resources of all types. There is more efficient algorithm by Habermann. Example . five processes: P 0 , P 1 , P 2 , P 3 , P 4 three resource types: A, B, C with 10, 5, 7 units. At time T 0 (Max = Allocation + Need)

46. Example Allocation Max Need Available A B C A B C A B C A B C P0 0 1 0 7 5 3 7 4 3 3 3 2 P1 2 0 0 3 2 2 1 2 2 P2 3 0 2 9 0 2 6 0 0 P3 2 1 1 2 2 2 0 1 1 P4 0 0 2 4 3 3 4 3 1 safe sequence <P1, P3, P4, P2, P0> Suppose that P1 requests (1,0,2). To decide whether or not to grant this request, Allocation Need P1 3 0 2 0 2 0 2 3 0 Again, safe seq <P1, P3, P4, P0, P2> In this new state, P4 requests (3,3,0) not enough available resources P0 requests (0,2,0) unsafe state? Why?