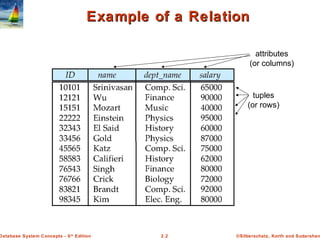
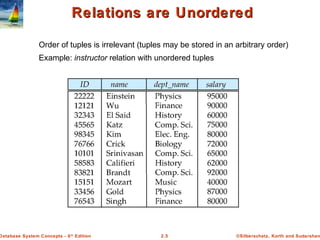
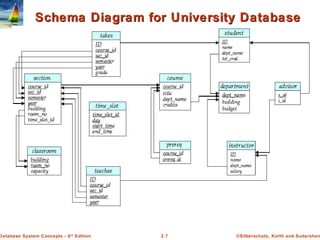
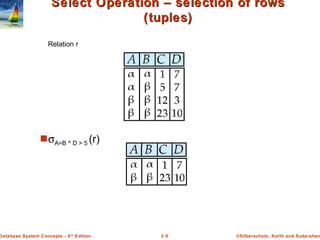
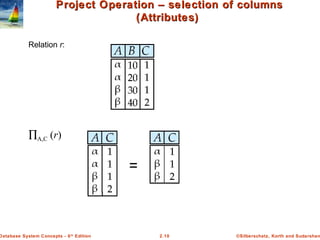
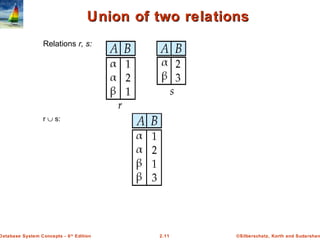
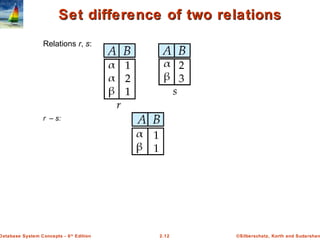
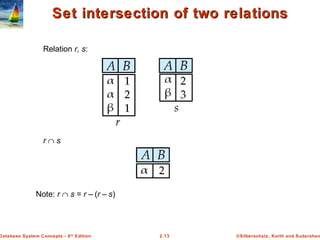
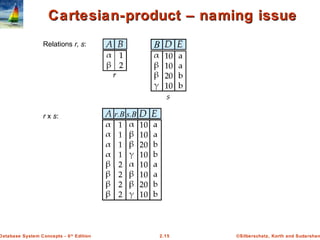
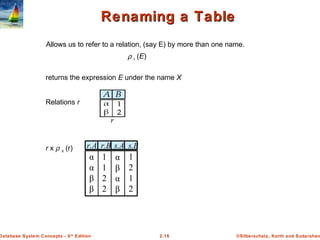
The document discusses key concepts of relational databases and relational algebra. It defines what a relation is as a set of tuples with attributes, and covers attribute types, keys, relations schemas and instances. It also summarizes the core relational algebra operations of selection, projection, join, union, difference and Cartesian product and how they are used to manipulate and query relations.