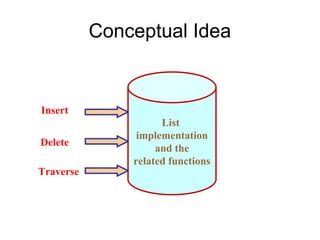
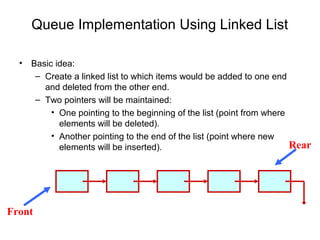
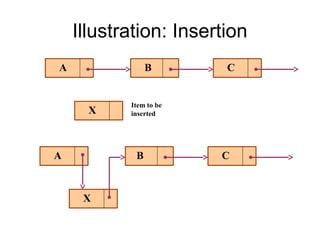
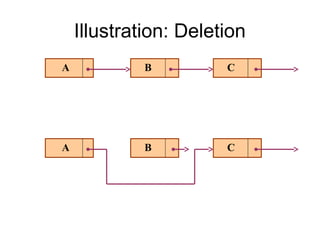
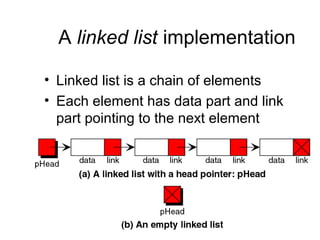
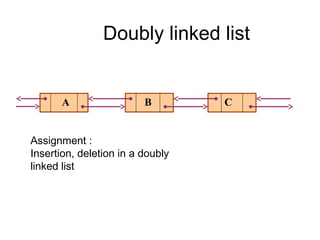
The document discusses data structures and abstract data types (ADTs). It provides examples of linear lists and linked lists as implementations of the ADT linear list. Key points made include: - An ADT defines operations on a data structure without specifying its implementation. - Linked lists provide flexibility for insertion and deletion compared to arrays. - The main linked list operations are insertion, deletion, finding an element, and traversal. 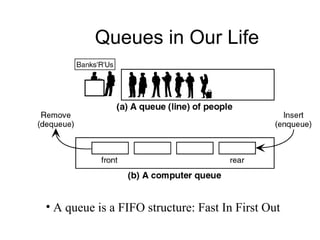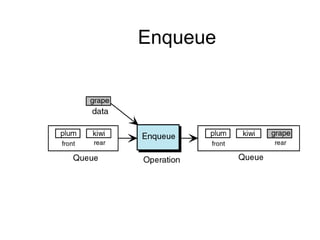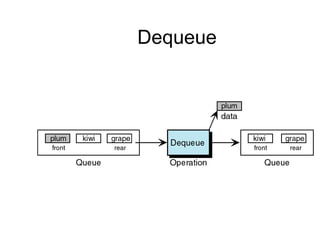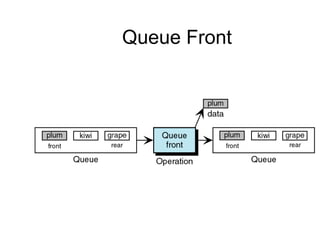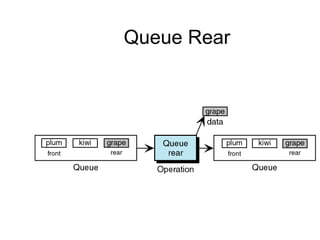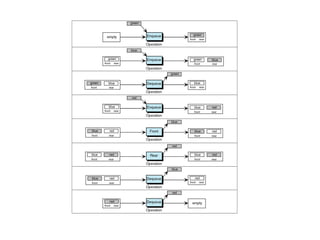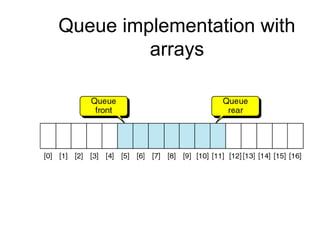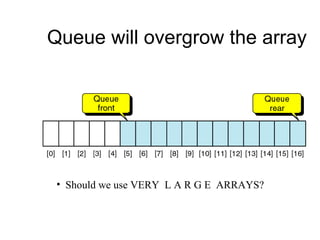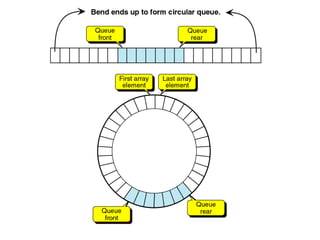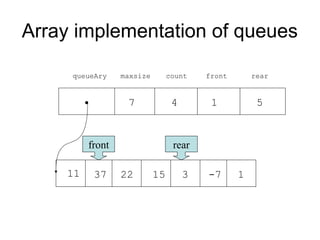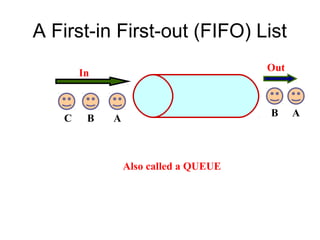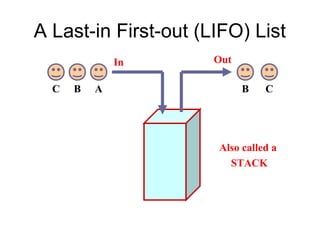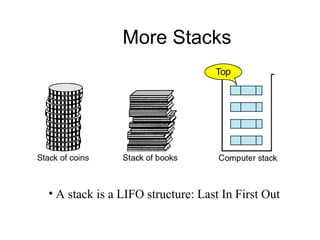- Queues and stacks are examples of linear lists with restricted insertion/deletion points.

1. Data Structures

2. Abstract Data Type
A collection of related data is known as
an abstract data type (ADT)
Data Structure = ADT + Collection of
functions that operate on the ADT

3. Data Structure
• Consist of the data structure definition
and a collection of functions that operate
on the struct
– We will never access the struct directly!

4. • Separate what you can do with data from
how it is represented
• Other parts of the program interacts with
data through provided operations
according to their specifications
• Implementation chooses how to represent
data and implement its operations

5. Multiple Implementations
• An ADT can have several implementations
• Interface functions are the same
• Application programs will not see any
difference

6. ADT: Linear list
• A sequence of elements
• There is first and last element
• Each element has previous and next
– Nothing before first
– Nothing after last

7. Why linked lists ?
• A linked list is a dynamic data structure.
– It can grow or shrink in size during the execution
of a program.
– It can be made just as long as required.
– It does not waste memory space.
• Linked lists provide flexibility in allowing the
items to be rearranged efficiently.
– Insert an element.
– Delete an element.

8. • What we can do with a linear list?
– Delete element
– Insert element
– Find element
– Traverse list

9. Illustration: Insertion
A B C
Item to be
X inserted
A B C
X

10. Illustration: Deletion
A B C
A B C

11. In essence ...
• For insertion:
– A record is created holding the new item.
– The next pointer of the new record is set to link it
to the item which is to follow it in the list.
– The next pointer of the item which is to precede it
must be modified to point to the new item.
• For deletion:
– The next pointer of the item immediately
preceding the one to be deleted is altered, and
made to point to the item following the deleted
item.

12. Traverse: list  elements in
order
• get_first(list) -
– returns first element if it exists
• get_next(list) -
– returns next element if it exists
• Both functions return NULL otherwise
• Calling get_next in a loop we will get one by one all
elements of the list

13. How we can implement a list?
• Array?
• Search is easy (sequential or binary)
• Traversal is easy:
for(i = first; i <= last; ++i)
process(a[i]);
• Insert and delete is not easy
– a good part of the array has to be moved!
• Hard to guess the size of an array

14. A linked list implementation
• Linked list is a chain of elements
• Each element has data part and link
part pointing to the next element

15. Main operations
• Create list
• Add node
– beginning,middle or end
• Delete node
– beginning,middle or end
• Find node
• Traverse list

16. Conceptual Idea
Insert
List
implementation
Delete
and the
related functions
Traverse

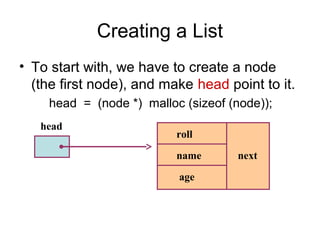
17. Example: Working with linked list
• Consider the structure of a node as follows:
struct stud {
int roll;
char name[25];
int age;
struct stud *next;
};
/* A user-defined data type called “node” */
typedef struct stud node;
node *head;

18. Creating a List
• To start with, we have to create a node
(the first node), and make head point to it.
head = (node *) malloc (sizeof (node));
head
roll
name next
age

19. Contd.
• If there are n number of nodes in the initial
linked list:
– Allocate n records, one by one.
– Read in the fields of the records.
– Modify the links of the records so that the
chain is formed.

20. void create_list (node *list)
{
int k, n;
node *p;
printf (“n How many elements?”);
scanf (“%d”, &n);
To be called from the main()
list = (node *) malloc (sizeof (node)); function as:
p = list;
for (k=0; k<n; k++) node *head;
{ …….
create_list (head);
scanf (“%d %s %d”, &p->roll,
p->name, &p->age);
p->next = (node *) malloc
(sizeof (node));
p = p->next;
}
free (p->next);
p->next = NULL;
}

21. Traversing the List
• Once the linked list has been constructed
and head points to the first node of the list,
– Follow the pointers.
– Display the contents of the nodes as they are
traversed.
– Stop when the next pointer points to NULL.

22. void display_list (node *list)
{
int k = 0;
node *p;
p = list;
while (p != NULL)
{
printf (“Node %d: %d %s %d”, k, p->roll,
p->name, p->age);
k++;
p = p->next;
}
}

23. Inserting a Node in the List
• The problem is to insert a node before a
specified node.
– Specified means some value is given for the
node (called key).
– Here it may be roll.
• Convention followed:
– If the value of roll is given as negative, the
node will be inserted at the end of the list.

24. • When a node is added at the beginning,
– Only one next pointer needs to be modified.
• head is made to point to the new node.
• New node points to the previously first element.
• When a node is added at the end,
– Two next pointers need to be modified.
• Last node now points to the new node.
• New node points to NULL.
• When a node is added in the middle,
– Two next pointers need to be modified.
• Previous node now points to the new node.
• New node points to the next node.

25. void insert_node (node *list)
{
int k = 0, rno;
node *p, *q, *new;
new = (node *) malloc (sizeof (node));
scanf (“%d %s %d”, &new->roll, new->name,
&new->age);
printf (“nInsert before roll (-ve for end):”);
scanf (“%d”, &rno);
p = list;
if (p->roll == rno) /* At the beginning */
{
new->next = p;
list = new;
}

26. while ((p != NULL) && (p->roll != rno))
{
q = p;
p = p->next;
}
The pointers q and p
if (p == NULL) /* At the end */ always point to
{
consecutive nodes.
q->next = new;
new->next = NULL;
}
if (p->roll == rno) /* In the middle */
{
q->next = new;
new->next = p;
}
}

27. Deleting an Item
• Here also we are required to delete a
specified node.
– Say, the node whose roll field is given.
• Here also three conditions arise:
– Deleting the first node.
– Deleting the last node.
– Deleting an intermediate node.

28. void delete_node (node *list)
{
int rno;
node *p, *q;
printf (“nDelete for roll :”);
scanf (“%d”, &rno);
p = list;
if (p->roll == rno) /* Delete the first element */
{
list = p->next;
free (p);
}

29. while ((p != NULL) && (p->roll != rno))
{
q = p;
p = p->next;
}
if (p == NULL) /* Element not found */
printf (“nNo match :: deletion failed”);
if (p->roll == rno) /* Delete any other element */
{
q->next = p->next;
free (p);
}
}

30. Doubly linked list
A B C
Assignment :
Insertion, deletion in a doubly
linked list

31. A First-in First-out (FIFO) List
Out
In
B A
C B A
Also called a QUEUE

32. A Last-in First-out (LIFO) List
In Out
C B A B C
Also called a
STACK

33. Stack

34. Stacks in Our Life

35. More Stacks
• A stack is a LIFO structure: Last In First Out

36. Basic Operations with Stacks
• Push
– Add and item
• Overflow
• Pop
– Remove an item
• Underflow
• Stack Top
– What’s on the Top
• Could be empty

37. Push
• Adds new data element to the top of the
stack

38. Pop
• Removes a data element from the top of
the stack

39. Stack Top
• Checks the top element. Stack is not
changed

41. push
pop
create
STACK
isempty
isfull

42. Assume:: stack contains integer elements
void push (stack s, int element);
/* Insert an element in the stack
*/
int pop (stack s);
/* Remove and return the top element */
void create (stack s);
/* Create a new stack */
int isempty (stack s);
/* Check if stack is empty */
int isfull (stack s);
/* Check if stack is full */

43. • We shall look into two different
implementations of stack:
– Using arrays
– Using linked list

44. Stack Implementation

45. Stack Implementation Using
Arrays
• Basic idea.
– Declare an array of fixed size (which
determines the maximum size of the stack).
– Keep a variable which always points to the
“top” of the stack.

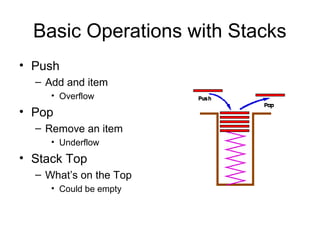
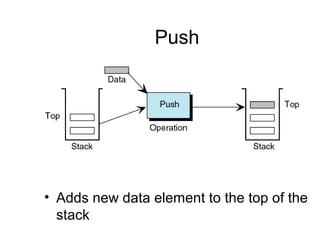
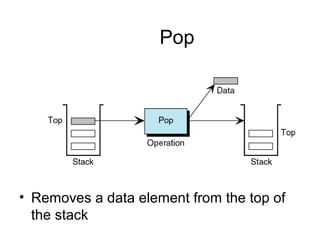
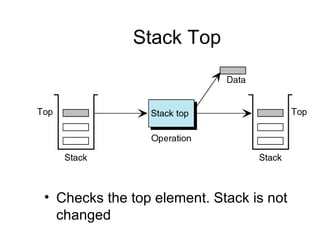
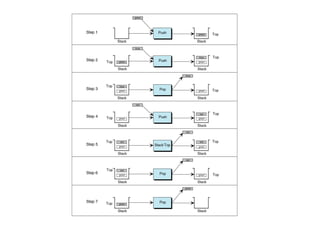
46. Declaration
#define MAXSIZE 100
struct lifo {
int st[MAXSIZE];
int top;
};
typedef struct lifo stack;

47. Stack Creation
void create (stack s)
{
s.top = 0; /* Points to last element
pushed in */
}

48. Pushing an element into the stack
void push (stack s, int element)
{
if (s.top == (MAXSIZE-1))
{
printf (“n Stack overflow”);
break;
}
else
{
s.top ++;
s.st [s.top] = element;
}

49. Removing/Popping an element from the stack
int pop (stack s)
{
if (s.top == 0)
{
printf (“n Stack underflow”);
break;
}
else
{
return (s.st [s.top --]);
}
}

50. Checking for stack full / empty
int isempty (stack s)
{
if (s.top == 0) return 1;
else return (0);
}
int isfull (stack s)
{
if (s.top == (MAXSIZE – 1)) return 1;
else return (0);
}

51. Stack Implementation Using
Linked List
• Very similar to the linked list
implementation discussed earlier.
struct lifo {
int element;
struct lifo *next;
};
typedef struct lifo stack;
stack *top;

52. Contd.
• Basic concept:
– Insertion (push) and deletion (pop) operations
take place at one end of the list only.
– For stack creation / push operation
• Required to call malloc function
– How to check stack underflow?
• Easy. Simply check if top points to NULL.
– How to check overflow?
• Check is malloc returns –1.

53. Sample Usage
stack A, B;
create (A); create (B);
push (A, 10); push (A, 20); push (A, 30);
push (B, 5); push (B, 25); push (B, 10);
printf (“n%d %d %d”, pop(A), pop(A), pop(A));
printf (“n%d %d %d”, pop(B), pop(B), pop(B));
if (not isfull (A)) 30 20 10
push (A, 50); 10 25 5
if (not isempty (A))
k = pop (A);

54. Queues

55. Queues in Our Life
• A queue is a FIFO structure: Fast In First Out

56. Basic Operations with Queues
• Enqueue - Add an item to the end of queue
• Overflow
• Dequeue - Remove an item from the front
• Could be empty
• Queue Front - Who is first?
• Could be empty
• Queue End - Who is last?
• Could be empty

57. Enqueue

58. Dequeue

59. Queue Front

60. Queue Rear

62. Queue implementation with
arrays

63. Queue will overgrow the array
• Should we use VERY L A R G E ARRAYS?

65. Array implementation of queues
queueAry maxsize count front rear
7 4 1 5
front rear
11 37 22 15 3 -7 1

66. Structure for a queue array
struct intqueue {
int *queueArray;
int maxSize;
int count;
int front;
int rear;
};

67. Queue Implementation Using Linked List
• Basic idea:
– Create a linked list to which items would be added to one end
and deleted from the other end.
– Two pointers will be maintained:
• One pointing to the beginning of the list (point from where
elements will be deleted).
• Another pointing to the end of the list (point where new
elements will be inserted). Rear
Front

68. Assume:: queue contains integer elements
void enqueue (queue q, int element);
/* Insert an element in the queue */
int dequeue (queue q);
/* Remove an element from the queue */
queue *create ();
/* Create a new queue */
int isempty (queue q);
/* Check if queue is empty */
int size (queue q);
/* Return the number of elements in queue */

69. Creating a queue
front = NULL;
rear = NULL;

70. Inserting an element in queue
void enqueue (queue q, int x)
{
queue *ptr;
ptr = (queue *) malloc (sizeof (queue));
if (rear == NULL) /* Queue is empty */
{
front = ptr; rear = ptr;
ptr->element = x;
ptr->next = NULL;
}
else /* Queue is not empty
*/
{
rear->next = ptr;
ptr ->element = x;
ptr->next = NULL;
}
}

71. Deleting an element from queue
int dequeue (queue q)
{
queue *old;
if (front == NULL) /* Queue is empty */
printf (“n Queue is empty”);
else if (front == rear) /* Single element */
{
k = front->element;
free (front); front = rear = NULL;
return (k);
}
else
{
k = front->element; old = front;
front = front->next;
free (old);
return (k);
}
}

72. Checking if empty
int isempty (queue q)
{
if (front == NULL)
return (1);
else
return (0);
}