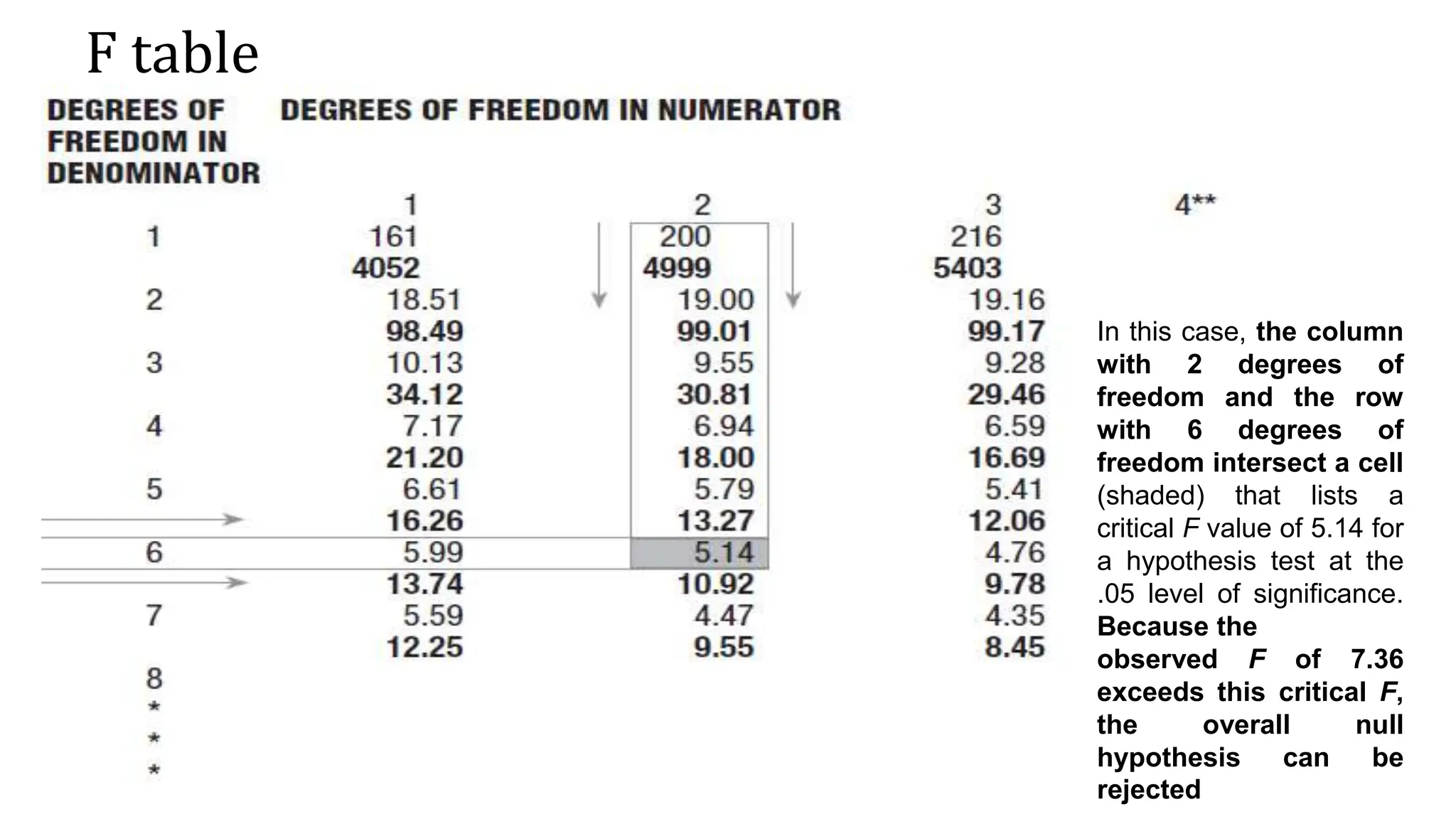
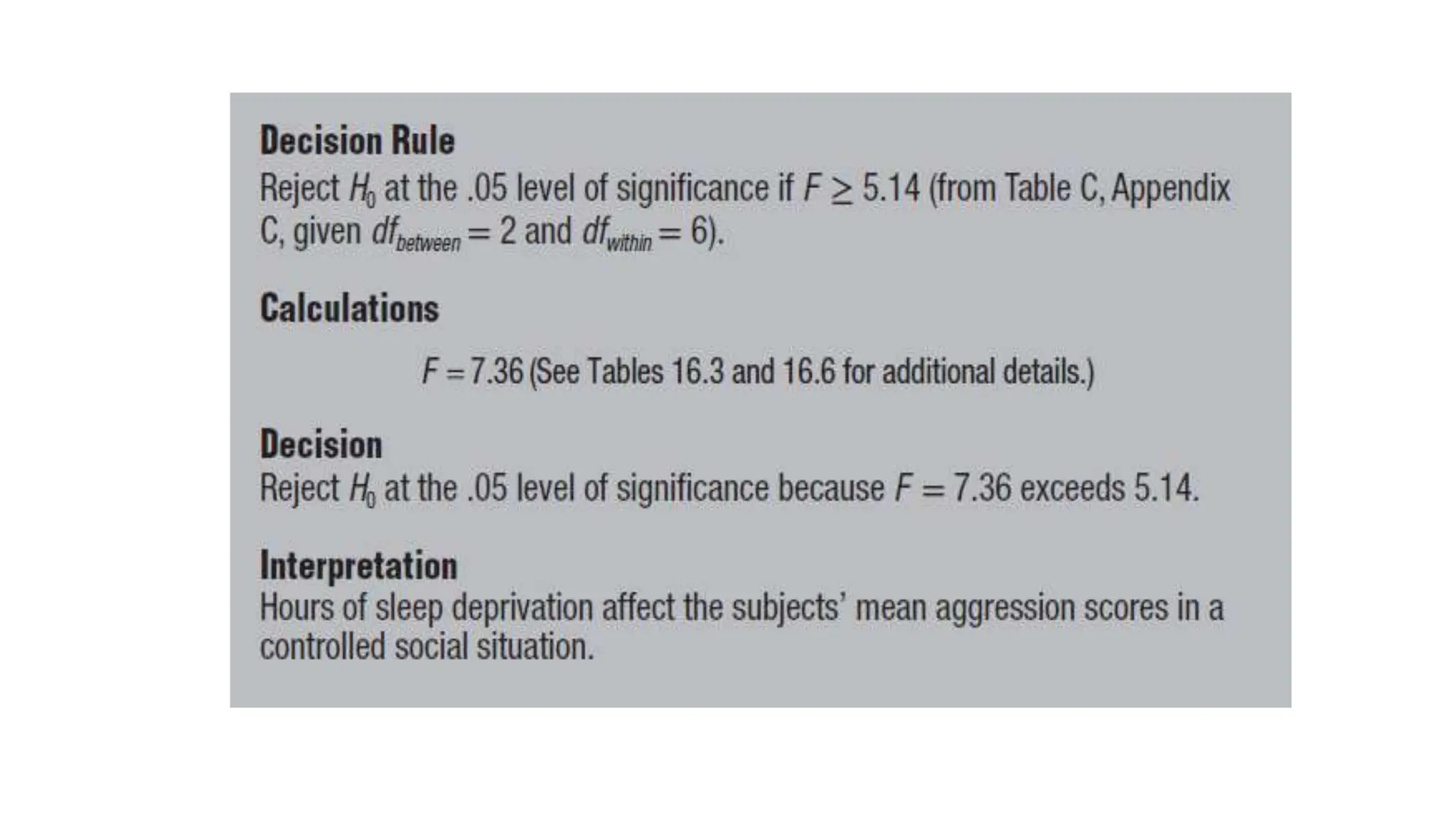
The document discusses two-factor ANOVA and the application of the F-test, using an example with critical values for hypothesis testing. It highlights that when the observed F value exceeds the critical value, the null hypothesis can be rejected. The calculations for degrees of freedom and the significance level are also detailed.

1. F-test – ANOVA – Two-factor experiments – three f-tests – two-factor
ANOVA –Introduction to chi-square tests..
Topics of Interest
1

2. Example Data

4. F table
In this case, the column
with 2 degrees of
freedom and the row
with 6 degrees of
freedom intersect a cell
(shaded) that lists a
critical F value of 5.14 for
a hypothesis test at the
.05 level of significance.
Because the
observed F of 7.36
exceeds this critical F,
the overall null
hypothesis can be
rejected

5. Computations

6. Computations

7. Formula for degrees of Freedom

8. Computations

10. Formula

11. Formula
Where
X = raw score
T = group total
n = group sample size
G = grand total
N = grand (combined) sample size

12. Formula

15. F table
In this case, the column
with 2 degrees of
freedom and the row
with 6 degrees of
freedom intersect a cell
(shaded) that lists a
critical F value of 5.14 for
a hypothesis test at the
.05 level of significance.
Because the
observed F of 7.36
exceeds this critical F,
the overall null
hypothesis can be
rejected