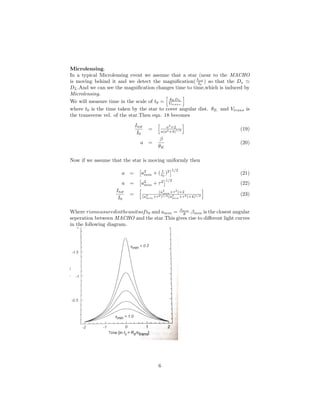
Detection Of Dark Matter (via Gravitational Lensing) This document discusses how gravitational lensing can be used to detect and measure the mass distribution of dark matter. It explains that dark matter does not emit light but will bend light passing nearby via its gravitational field based on general relativity. Precise measurements of the bending angle using the lens equation can reveal the Einstein angle and corresponding dark matter mass distribution. Microlensing observations of stars in nearby galaxies magnified by potential dark matter candidates like MACHOs moving in galactic halos can reveal characteristic light curves used to detect dark matter presence and estimate its mass.

1. Detection Of Dark Matter
(via Gravitational Lensing)
Arkajyoti Manna∗
Dept. of Physics
Ramakrishna Mission Vivekananda University
Belur,India
April 29, 2015
Abstract
Since the study of galaxy rotation curve by Vera C. Rubin et.al ,there
was an indication that there is a massive amount of mass exists in our
universe which is not visible to us.Apart from Flat Galaxy Rotation curve
there are several other experiments which confirm the existance of the
so called dark matter.In this article we discuss how can one predict the
existance of dark matter and the mass distribution for it(only for sim-
ple cases) via Gravitational Lensing.We will use the bending of light
phenomenon predicted by General relativity.
1 Galaxy Rotation curve
Let us consider a spiral galaxy whose shape is like a disk of total mass Mr .If
the rotational velocity of a body near the edge of the galaxy vr of mass m,at a
distance r from the center of the disk.Then using Newtons Law of Gravitation
it can be shown that
mv2
r
r
=
GMrm
r2
⇒ vr =
GMr
r
(1)
The dotted one is Keplerian orbital velocity distribution and solid one is the
observed one .
∗arkajyoti1@live.com
1

2. This is seen for several other galaxies also.
This indicates there exists a huge amount of mass in the halo of a galaxy.As the
dark matter does’nt emit any kind of electromagnetic radiation there is no way
to see it(that’s why it is dark).But general relativity tells us that any kind of
mass(visible or not!) will produce curvature which can bend light coming from
any luminous source(i.e;stars,galaxies).We will use this idea in the next section.
2 Gravitational Lensing
From the study of null geodesics in Schwarzschild spacetime that light will bent
when it passes near any massive object by some definite amount corresponding
to its mass.It can be shown that the angle of deflection is given by
φbend =
2rs
b
(2)
where rs = 2GM
c2 ;rs and M stands for the Schwarzschild radius and mass of the
lensing body respectively.
2.1 Lens equation
We set up an equation relating the angular seperation of the source,it’s images
and the position of lens and observer.
2

3. Where observer O and lens L are on same axis.S is the source of light and I is
it’s image.For simplcity we will assume that the source and it’s image are in the
plane ⊥ to the lens-obs. axis(as the corresponding angles are so small that the
corection due to this are also small).As the various angles are so small,we will
use tanθ θ.
If α is the total deflection of light,then by inspection,it is evident that
θDs = βDs + (α1 + α2)DLS (3)
α1 + α2 = α (4)
α =
2rs
b
(5)
Here ”b” is the distance between the light ray at ∞ and lens.As the deviation
is in the order of arc-sec we approximately write b ξ.then
α =
2rs
ξ
(6)
θ = β +
1
θ
(2rsDLS
DLDs
)
1
2
2
(7)
θ = β +
1
θ
θE
2
(8)
θE = 2rsDLS
DLDs
1/2
(9)
(10)
3

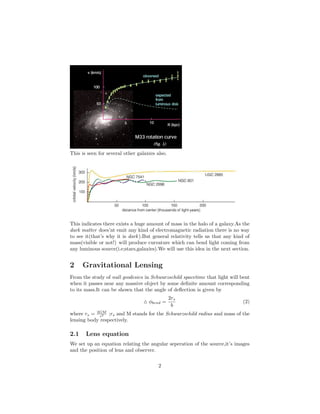
4. where θE is the Einstein angle. As the eqn.8 is quadratic in θ,so we will get
two images at an angular seperation
θ± =
1
2
[β ± (β2
+ 4θ2
E)1/2
] (11)
So clearly θ+ > 0 and θ− < 0.Hence we will get two images on two opposite
sides of L-O axis.Now if have these angles measurd and the angle between S and
O(β) then we have the Einsetin Angle(θE).And the mass of the lensing body
can be found by using eqn.9 as
rS =
2GML
c2
(12)
Typically for the lensing of a source by a galaxy (both at cosmological distance
1Gpc) the θE=1 arc-sec.But for a star (of mass nearly to our sun) within the
galaxy θE = 10−3
arc-sec, which can not be detected in contemporary telescopes.
But to detect and know the mass distribution of Dark matter in the halo of
galaxy we have to measure the Einstein angle θE.And the technique is called
Microlensing.Here we will not discuss the Strong lensing for which constrain
the Dark energy and the mass distribution of Dark matter.
2.2 Microlensing
If Prad⇒ Power radiated by the source isotropically and Ω is the solid angle
subtended by detector,then
dPrad
dΩ
= S. ˆRR2
(13)
(14)
where is Poynting vector.As the intensity I ∝ dPrad
R2 then we can write
I = S. ˆRdΩ.Then
I = k Ω (15)
where k is called surface brightness of the source(directly depenpends only on
source) and can not be affected by Gravitational lensing.The following diagram
may be helpful.
4

5. where MACHO(Massive Compact Halo object) is one of the possible candidate
for Dark matter,which moves in the halo of a galaxy.
The intensity due to the lens increases as more light rays comes to the earth
based detector than without the lens.Then(as the angular spread of the source
is preseved)
I±
I0
=
Ω±
Ω0
= (θ±/β)(dθ±/dβ) (16)
I±
I0
=
1
4
β
(β2+4θ2
E )1/2 +
(β2
+4θ2
E )
1/2
β ± 2 (17)
So the total intensity Itot(I+ + I−) is given by
Itot
I0
=
1
2
β
(β2+4θ2
E )1/2 +
(β2
+4θ2
E )
1/2
β
(18)
so we can make the brightness better by making the angle β small.This is ex-
tremely usefull when the two images can not be resolved in contemporary tele-
scopes.
2.3 Massive Compact Halo Object(MACHO)
As said before MACHO is one of the possible canditate for Dark matter.MACHO
consists of brown dwarfs,white dwarfs,small black holes,dead stars,etc which
moves in the halo of galaxy.Suppose there is a situation when a MACHO moves
close to a star in a nearby galaxy of ours(such as Large Magellanic Cloud) then
due to MACHO’s mass we see lensing of that star.For this we essentially need
5

6. Microlensing.
In a typical Microlensing event we assume that a star (near to the MACHO
is moving behind it and we detect the magnification(Itot
I0
) so that the Ds
DL.And we can see the magnification changes time to time,which is induced by
Microlensing.
We will measure time in the scale of t0 = θE DL
Vtrans.
where t0 is the time taken by the star to cover angular dist. θE. and Vtrans is
the transverse vel. of the star.Then eqn. 18 becomes
Itot
I0
= a2
+2
a(a2+4)1/2 (19)
a =
β
θE
(20)
Now if we assume that the star is moving uniformly then
a = a2
min + ( t
t0
)2 1/2
(21)
a = a2
min + τ2 1/2
(22)
Itot
I0
= (a2
min+τ2
)+2
(a2
min+τ2)1/2(a2
min+τ2)+4)1/2 (23)
Where τismeasuredintheunitsoft0 and amin = βmin
θ .βmin is the closest angular
seperation between MACHO and the star.This gives rise to different light curves
in the following diagram.
6

7. 3 Conclusion
In this article we only have discussed one of the possible canditate for Dark
matter i,e. MACHO.But recent studies shows that Dark matter is consists of
WIMP(Weakly Interacting Massive Particle) to a large proportion and from
various criterion WIMPs are very eligible canditate for Dark matter(which goes
beyond of our present discussion).
4 Reference
1.Gravity:An Introduction to Einstein’s General Relativity :James Hartle
2.General Relativity :Straumann
7