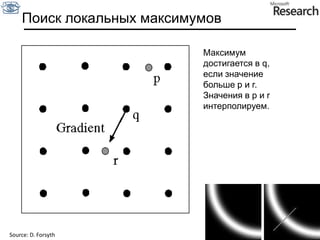
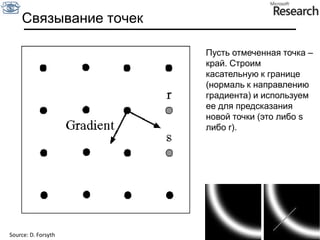
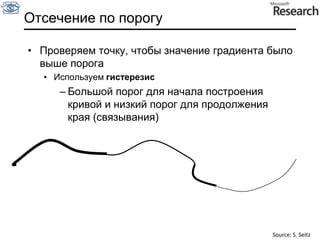
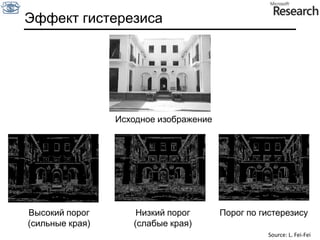
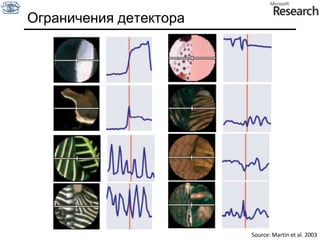
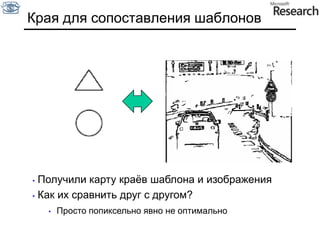
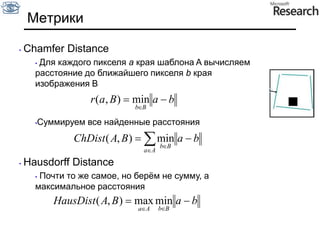
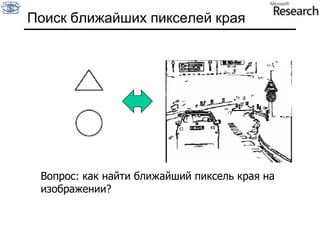
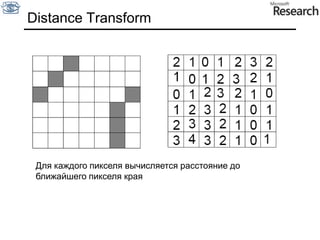
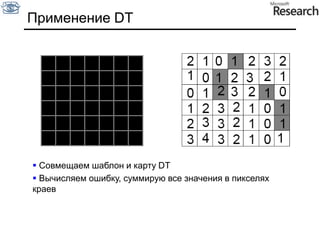
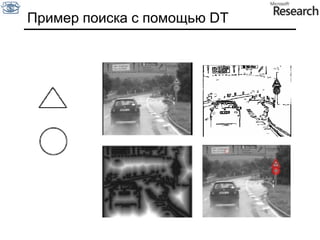
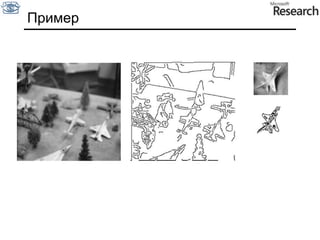
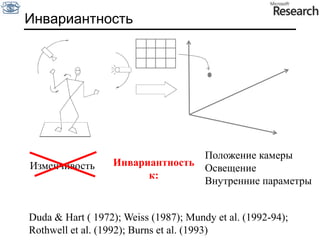
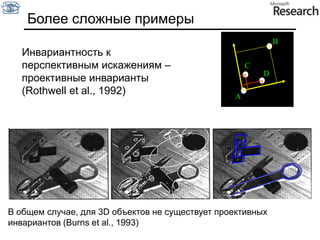
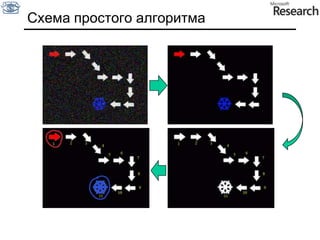
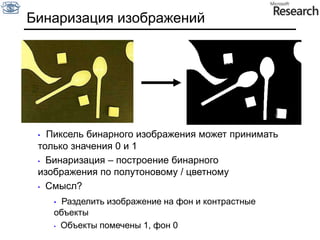
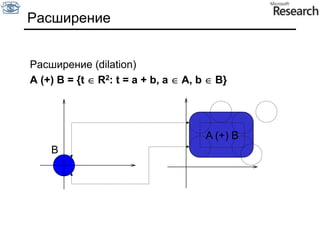
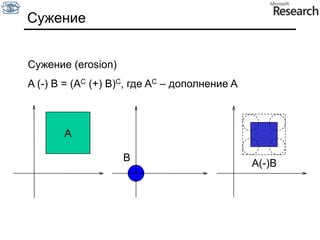
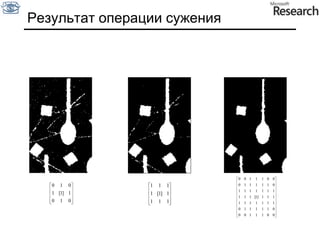
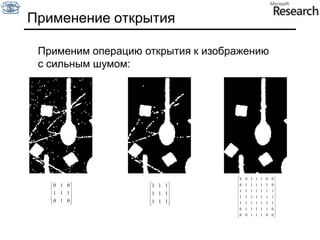
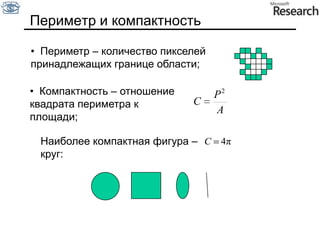
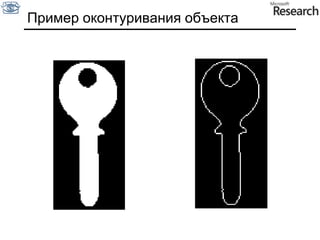
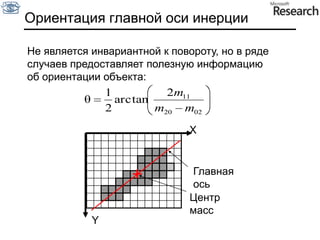
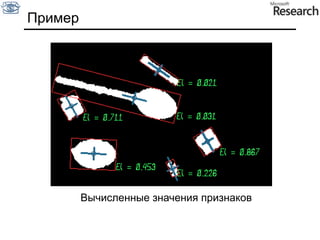
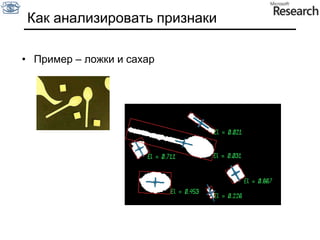
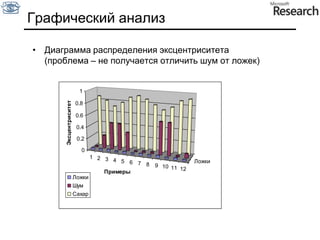
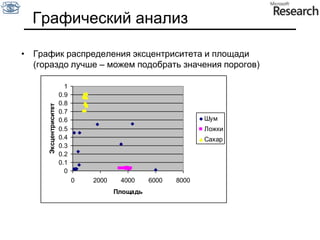
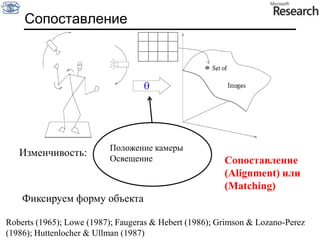
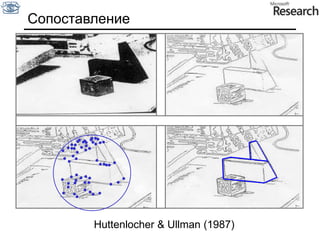
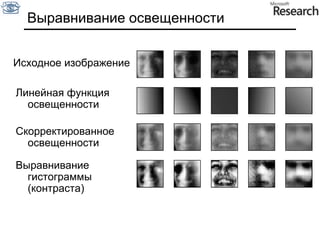
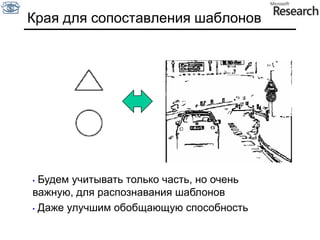
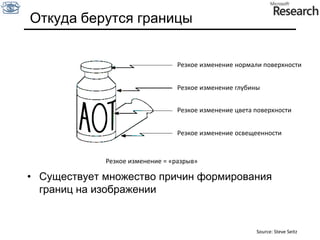
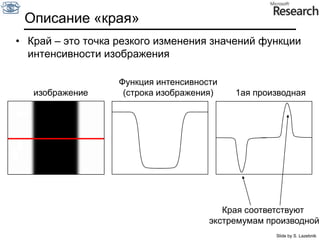
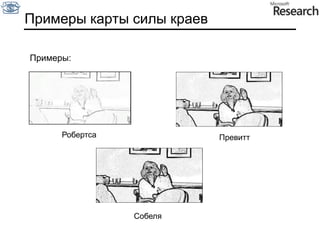
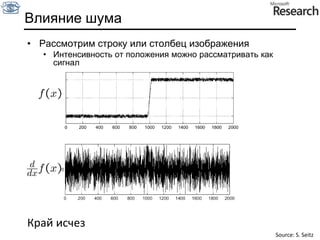
Документ представляет собой курс по анализу изображений, охватывающий методы сопоставления шаблонов и выделения краев. Описываются различные подходы к обработке изображений, включая нормализацию освещения, использование градиентов и методы бинаризации, а также проблемы, возникающие при анализе изображений. Основное внимание уделяется разработке детекторов краев и методам оценки качества детекторов.

1. Простой анализ изображенийMany slides adapted from Fei-Fei Li, Rob Fergus, Antonio Torralba, Jean Ponce and Svetlana Lazebnik

2. Общая информацияЭтот курс подготовлени читается при поддержкеСтраница курсаhttp://courses.graphicon.ru/main/vision

3. Изменчивость изображенийПоложение камерыОсвещениеВнешние факторы:Внутренние факторы:Внутриклассовая изменчивость

4. Внутриклассовая изменчивость

5. СопоставлениеqПоложение камерыОсвещениеИзменчивость:Сопоставление(Alignment) или (Matching)Фиксируем форму объектаRoberts (1965); Lowe (1987); Faugeras & Hebert (1986); Grimson & Lozano-Perez (1986); Huttenlocher & Ullman (1987)

6. СопоставлениеL. G. Roberts, Machine Perception of Three Dimensional Solids, Ph.D. thesis, MIT Department of Electrical Engineering, 1963.

7. СопоставлениеHuttenlocher & Ullman (1987)

8. Сопоставление шаблоновФиксируем объектОпишем объект его изображением – шаблоном (pattern)Хотим найти объект в изображенииОграничим возможные преобразования (внешние факторы)Сдвиг, размер, поворотОсвещение?Будем искать объект в изображении путём попиксельного сравнения шаблона и всех фрагментов изображения«Pattern matching»

9. Метрики(SAD) Sum of absolute differences(SSD) Sum of squared differences(CC) Cross-correlationSAD, SSD – минимизируются (0 – точное совпадение)

10. CC – максимизируется (1 – точное совпадение)Нормализация освещенностиОсвещённость может менятьсяМожно нормализовать интенсивности пикселей шаблона и фрагмента изображенияСредняя интенсивностьНорма интенсивности окнаНормализованный пиксель

11. Выравнивание освещенностиИсходное изображениеЛинейная функция освещенностиСкорректированное освещенностиВыравнивание гистограммы (контраста)

12. Пример: пульт ТВ Шаблон (слева), изображение (в центре), карта нормализованной корреляции (справа)

13. Пик яркости (максимум корреляции) соответствует положению руки (искомого шаблона)Пример: пульт ТВ

14. Пример: пульт ТВ

15. Пример: пульт ТВ

16. Пример: пульт ТВ

17. Ограничения и проблемыИщем конкретный объект, а не класс / категорию объектов

18. Не «символ», а конкретную букву в конкретном шрифте

19. Трудоёмкость

20. Полный перебор параметров

21. Модель преобразования

22. В простом варианте неизвестно только положение, размер и ориентация фиксированы

23. Чтобы учесть поворот и ориентацию придётся перебрать все возможные параметры

24. Шаблонов может быть много

25. OCR – распознавание символов

26. По шаблону на каждый символКак улучшить подход?

27. Поиск краевИнтуитивно понятно, что основная информация в картинке содержится как раз в границах (краях)Компактное представлениеСоответствует устройству мозгаЗадача: Выделить резкие изменения (разрывы) изображения Идеал:рисунок художника (но артист уже пользуются своими знаниями об объектах)Source: D. Lowe

28. Края для сопоставления шаблонов Будем учитывать только часть, но очень важную, для распознавания шаблонов

29. Даже улучшим обобщающую способностьОткуда берутся границыРезкое изменение нормали поверхностиРезкое изменение глубиныРезкое изменение цвета поверхностиРезкое изменение освещеенностиРезкое изменение = «разрыв»Существует множество причин формирования границ на изображенииSource: Steve Seitz

30. Функция интенсивности(строка изображения)1ая производнаяКрая соответствуют экстремумам производнойОписание «края»Край – это точка резкого изменения значений функции интенсивности изображенияизображениеSlide by S. Lazebnik

31. Градиент изображенияГрадиент изображения: Градиент направлен в сторону наибольшего изменения интенсивностиНаправления градиента задается как:Как направление градиента соответствует направлению края?

32. Сила края задается величиной (нормой) градиента:Source: Steve Seitz

33. Дифференцирование и свёртка Разностная производная: Свёртка!Для функции 2х переменных, f(x,y):Линейная и инвариантная к переносу, поэтому м.б. Результатом сверткиSource: D. Forsyth, D. Lowe

34. Вычисление градиентаСемейство методов основано на приближенном вычисление градиента, анализе его направления и абсолютной величины. Свертка по функциям:ПревиттСобеляРобертсаМатематический смысл – приближенное вычисление производных по направлению

35. Примеры карты силы краевПримеры:РобертсаПревиттСобеля

36. Край исчезВлияние шумаРассмотрим строку или столбец изображенияИнтенсивность от положения можно рассматривать как сигналSource: S. Seitz

37. Влияние шумаРазностные производные очень чувствительны к шумуЗашумленные пиксели отличаются от соседейЧем сильнее шум, тем выше откликСглаживаниеСглаживание делает все пиксели (зашумленные?) чуть более похожими на соседейSource: D. Forsyth

38. Предобработка (сглаживание)gf * gДля поиска краев ищем пики в:fSource: S. Seitz

39. fСвойства сверткиОперации свертки и дифференцирования ассоциативны:Это экономит 1 операцию:Source: S. Seitz

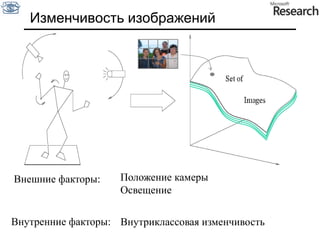
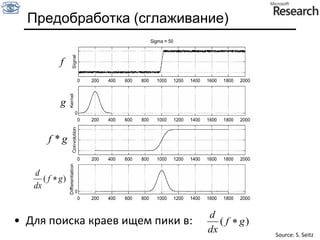
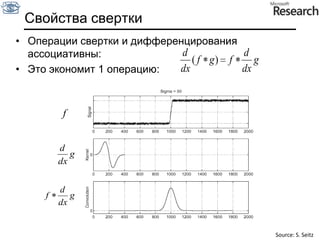
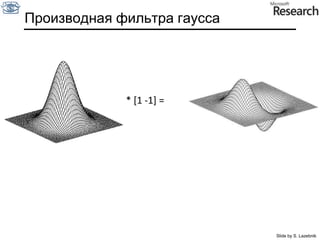
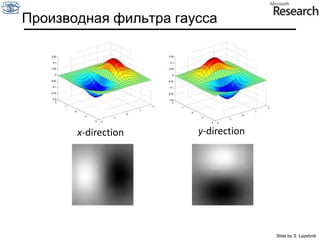
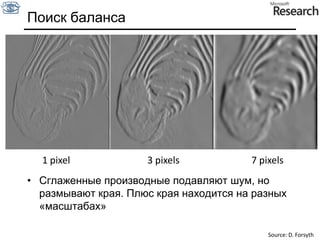
40. Производная фильтра гаусса* [1 -1] = Slide by S. Lazebnik

41. Производная фильтра гауссаy-directionx-directionSlide by S. Lazebnik

42. Поиск баланса1 pixel3 pixels7 pixelsСглаженные производные подавляют шум, но размывают края. Плюс края находится на разных «масштабах»Source: D. Forsyth

43. Исходное изображениеВыделение краевВычисление градиента – это еще не всё…

44. Чего не хватает?

45. Точности – края «толстые» и размытые

46. Информации о связности Карта силы краев

47. Разработка детектора краевКритерии качества детектора:Надежность:оптимальный детектор должен редко ошибаться (ложные края и пропущенные края) Точная локализация:найденный край должен быть как можно ближе к истинному краюЕдинственный отклик:детектор должен выдавать одну точку для одной точки истинного края, т.е. локальных максимум вокруг края должно быть как можно меньшеСвязанность: хотим знать, какие пиксели принадлежат одной линии краяSource: L. Fei-Fei

48. Детектор CannyСвертка изображения с ядром – производной от фильтра гауссаПоиск нормы и направления градиентаВыделение локальных максимумов (Non-maximum suppression)Утоньшение полос в несколько пикселей до одного пикселя Связывание краев и обрезание по порогу (гистерезис) :Определяем два порога: нижний и верхнийВерхний порог используем для инициализации кривыхНижний порог используем для продолжения кривыхMATLAB: edge(image, ‘canny’)Source: D. Lowe, L. Fei-Fei

49. ПримерИсходное изображение (Lena)Slide by S. Lazebnik

50. ПримерНорма градиентаSlide by S. Lazebnik

51. ПримерОтсечение по порогуSlide by S. Lazebnik

52. ПримерУтоньшение(non-maximum suppression)Slide by S. Lazebnik

53. Поиск локальных максимумовМаксимум достигается в q, если значение больше p и r. Значения в p и r интерполируем. Source: D. Forsyth

54. Связывание точекПусть отмеченная точка – край. Строим касательную к границе (нормаль к направлению градиента) и используем ее для предсказания новой точки (это либо s либо r). Source: D. Forsyth

55. Отсечение по порогуПроверяем точку, чтобы значение градиента было выше порогаИспользуем гистерезисБольшой порог для начала построения кривой и низкий порог для продолжения края (связывания)Source: S. Seitz

56. Высокий порог(сильные края)Низкий порог(слабые края)Порог по гистерезисуЭффект гистерезисаИсходное изображениеSource: L. Fei-Fei

57. Влияние Canny with original Canny with Выбор (размера ядра размытия) зависит от задачибольшое- поиск крупных границ

58. малая- выделение мелких деталейSource: S. Seitz

59. Ограничения детектораSource: Martin et al. 2003

60. Поиск краев – это только начало…human segmentationimagegradient magnitudeBerkeley segmentation database:http://www.eecs.berkeley.edu/Research/Projects/CS/vision/grouping/segbench/Slide by S. Lazebnik

61. Края для сопоставления шаблонов Получили карту краёв шаблона и изображения

62. Как их сравнить друг с другом?

63. Просто попиксельно явно не оптимальноМетрикиСhamfer Distance

64. Для каждого пикселя aкрая шаблона A вычисляем расстояние до ближайшего пикселяb края изображения B

65. Суммируем все найденные расстояния

66. Hausdorff Distance

67. Почти то же самое, но берём не сумму, а максимальное расстояния Метрики Свойства метрик

68. Сhamfer требует нормализации, Hausdorffнет

69. Chamfercимметрична, Hausdorffнет

70. HausDist (A,B) <> HausDist(B,A)

71. Можно использовать не max, а медиану (медленнее)

72. Какую метрику использовать?

73. Обычно заранее сказать нельзя, нужна экспериментальная проверка Поиск ближайших пикселей краяВопрос: как найти ближайший пиксель края на изображении?

74. Distance TransformДля каждого пикселя вычисляется расстояние до ближайшего пикселя края

75. Применение DT Совмещаем шаблон и карту DT

76. Вычисляем ошибку, суммирую все значения в пикселях краевПростейший алгоритм – N проходов

77. Первый проход помечает края 0

78. На втором помечаем все граничащие с 0 пиксели как 1

79. И т.д.

80. Существует двухпроходный алгоритмВычисление DT

81. Пример DTDT может использоваться для поиска «скелета» – осей объекта

82. Пример поиска с помощью DT

83. Пример

84. Резюме сопоставления шаблоновПодходит в тех случаях, когда объекты фиксированы и модель преобразования не очень сложная

85. Цифры на знаках

86. Цифры на конвертах

87. Аэрофотосъёмка / Космическая съёмка

88. Не очень быстрые методы

89. Требуются специальные процедуры для ускорения, пр. отбраковка ложных фрагментов по упрощённым критериям и т.д.Номера

90. ИнвариантностьПоложение камерыОсвещениеВнутренние параметрыИнвариантностьк:ИзменчивостьDuda & Hart ( 1972); Weiss (1987); Mundy et al. (1992-94);Rothwell et al. (1992); Burns et al. (1993)

91. ПримерыЛожки и сахарКлетки кровиНомераМонеты и купюрыКонтрастные объекты на фоне!

92. Более сложные примерыBИнвариантность к перспективным искажениям – проективные инварианты (Rothwell et al., 1992)CDAВ общем случае, для 3D объектов не существует проективных инвариантов(Burns et al., 1993)

93. Схема простого алгоритма

94. Схема простого алгоритма Предобработка изображения для упрощения анализа (например – шумоподавление)

95. Выделение на изображении контрастных областей-кандидатов в которых может находится искомый объект

96. Вычисление признаков (инвариантов) по выделенным фрагментам

97. Проверка – является ли фрагмент изображения изображением нужного нам объекта по измеренным параметрамБинаризация изображенийПиксель бинарного изображения может принимать только значения 0 и 1

98. Бинаризация – построение бинарного изображения по полутоновому / цветному

99. Смысл?

100. Разделить изображение на фон и контрастные объекты

101. Объекты помечены 1, фон 0Пороговая фильтрация Простейший вариант - пороговая фильтрация (thresholding)

102. Выделение областей, яркость которых выше/ниже некоторого порога, заданного «извне»Пороговая фильтрацияБолее интересный способ – определение порога автоматически, по характеристикам изображения Анализ гистограммы Анализ гистограммыАнализ симметричного пика гистограммы

103. Применяется когда фон изображения дает отчетливый и доминирующий пик гистограммы, симметричный относительно своего центра.Сгладить гистограмму;Найти ячейку гистограммы hmax с максимальным значением;На стороне гистограммы не относящейся к объекту (на примере – справа от пика фона)найти яркость hp, количество пикселей с яркостью >= hpравняется p% (например 5%) от пикселей яркости которых >= hmax;Пересчитать порог T =hmax- (hp - hmax);

104. Адаптивная бинаризация Необходима в случае неравномерной яркости фона/объекта.

105. Адаптивная бинаризация Необходима в случае неравномерной яркости фона/объекта.Для каждого пикселя изображения I(x, y):В окрестности пикселя радиуса rвысчитывается индивидуальный для данного пикселяпорог T;Если I(x, y) > T + C , результат 1, иначе 0;Варианты выбора T:T = mean

106. T = median

107. T = (min + max) / 2Адаптивная бинаризацияr=7, C=7r=75, C=10Исходноеr=7, C=0

108. Шум в бинарных изображенияхПример бинарного изображению с сильным шумомЧасто возникает из-за невозможности полностью подавить шум в изображениях, недостаточной контрастности объектов и т.д.

109. Шум в бинарных изображениях По одному пикселю невозможно определить – шум или объект?

110. Нужно рассматривать окрестность пикселя!Подавление и устранение шумаШироко известный способ - устранение шума с помощью операций математической морфологии: Сужение (erosion)

111. Расширение (dilation)

112. Закрытие (closing)

113. Раскрытие (opening)Математическая морфологияABМножество A обычно является объектом обработки, а множествоB (называемое структурным элементом) – инструментом.

114. Расширение в дискретном случаеBA(+)BAОперация «расширение» - аналог логического «или»

115. РасширениеРасширение (dilation)A (+) B = {t  R2: t = a + b, a  A, b  B}A (+) BB

116. CужениеСужение (erosion)A (-) B = (AC(+) B)С, где AC – дополнение AABA(-)B

117. Результат операции сужения