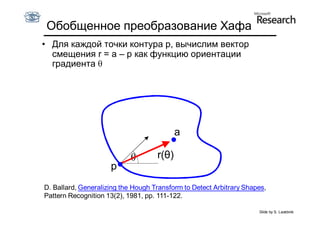
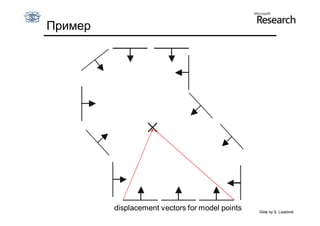
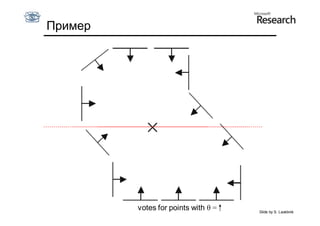
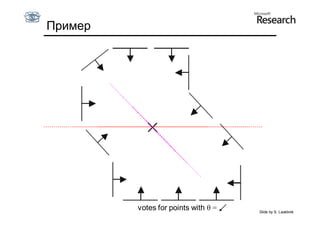
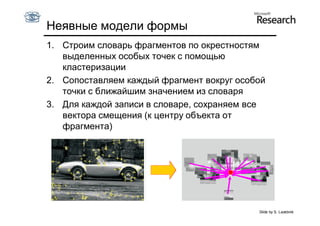
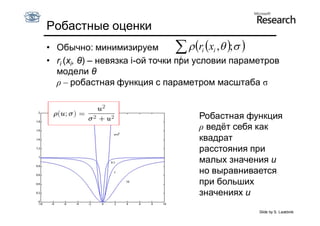
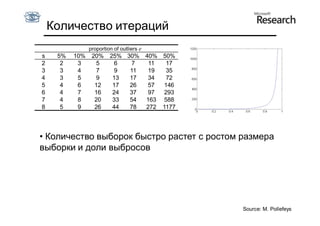
Документ обсуждает методы оценки параметров для различных моделей, с акцентом на применение метода наименьших квадратов и робастных оценок для обработки шумных данных и выбросов. Основные вопросы, рассматриваемые в документе, включают выбор наилучшей модели для описания набора признаков и обработку отклонений в данных. Также подробно освещаются алгоритмы, такие как RANSAC и преобразование Хафа, для нахождения оптимальных параметров линий и конусов.




















![Наименьшие квадраты для коники
• Формула коники:
C(a, x) = a · x = ax2 + bxy + cy2 + dx + ey + f = 0,
a = [a, b, c, d, e, f],
x = [x2, xy, y2, x, y, 1]
• Минимизация геометрических расстояний –
нелинейная оптимизация даже для коник
• Алгебраическое расстояние: C(a, x)
• Алгебраическое расстояние минимизируется НК:
a
x12
x1 y1 y12 x1 y1 1 b
2 2
x2 x2 y2 y2 x2 y2 1 c
0
d
2 2
xn
xn yn yn xn yn 1 e
f
Slide by S. Lazebnik](https://image.slidesharecdn.com/cv201106fitting-110629035436-phpapp01/85/CV2011-Lecture-6-Fitting-24-320.jpg)














































![Дискретизация
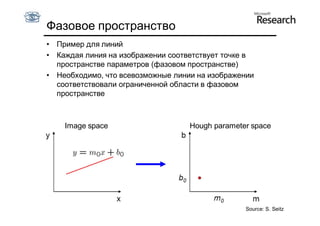
Переводим непрерывное фазовое
пространство в дискретное:
• введем сетку на пространстве (R, )
Счетчик ставится в соответствие каждой ячейке сетки
[Ri, Ri+1] x [i,i+1]
За эту ячейку «голосуют» точки (x, y), удовлетворяющие:
x cos + y sin = R, где i ≤ ≤ i+1, Ri ≤ R ≤ Ri+1](https://image.slidesharecdn.com/cv201106fitting-110629035436-phpapp01/85/CV2011-Lecture-6-Fitting-79-320.jpg)