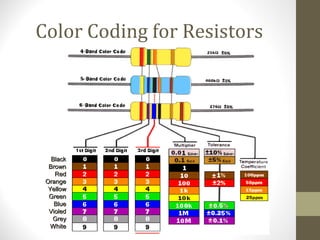
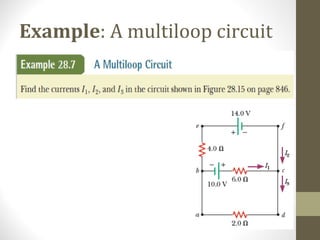
1) The document provides information about physics concepts related to electric current and resistors, including definitions of current, resistance, Ohm's Law, and Kirchhoff's rules. 2) Formulas are given for calculating current, resistance, power, and equivalent resistance for resistors connected in series and parallel. 3) Examples are included to demonstrate applying the concepts and formulas to calculate values like current, resistance, and power in electric circuits.

1. 203 PHYS - Physics 2203 PHYS - Physics 2
(for Engineering)(for Engineering)
Instructor:
Dr. Sabar Hutagalung
Physics Department, Faculty of Science, Jazan University
Jazan, Saudi Arabia
Email: sdhutagalung@gmail.com

2. CURRENT AND
RESISTORS

3. Main ReferenceMain Reference
• Raymond A. Serway & John W. Jewett, Jr., Physics for
Scientists and Engineers with Modern Physics, 9th Edition,
Brooks/Cole, 2014.

4. Electric Current
• The average current Iavg is equal to the
charge that passes through A per unit
time:
• The instantaneous current I as the limit of
the average current as ∆t → 0:
• The SI unit of current is the ampere (A): 1 A = 1 C/s1 A = 1 C/s

5. Microscopic Model of Current
• The total charge ∆Q in this segment is
• The average current in the conductor is
• where q is the charge, n is number of charge, vd is called the
drift speed - the speed of the charge, A is crossectional area.

6. Quiz
Answer:
IIaa >> IIbb == IIcc >> IIdd

7. Example
• The 12-gauge copper wire in a typical residential building has
a cross-sectional area of 3.31 x 1026
m2
. It carries a constant
current of 10.0 A. What is the drift speed of the electrons in
the wire? Assume each copper atom contributes one free
electron to the current. The density of copper is 8.92 g/cm3
.

8. Solution
• Use the molar mass and the density of copper to find the
volume of 1 mole of copper:
• The drift speed and substitute for the electron density:

9. Resistance
• Because current is
• Then, the current density, J:
• where the constant of proportionality σ is called the
conductivityconductivity.
Ohm’s law:
““For many materials (including most metals), the ratio ofFor many materials (including most metals), the ratio of
the current density to the electric field is a constantthe current density to the electric field is a constant σσ
that is independent of the electric field producing thethat is independent of the electric field producing the
current.”current.”

10. Resistance
• Potential difference
R is called the resistance.
Unit of R is volt per ampere
which defined to be ohm (Ω):
1 Ω = 1 V/A

11. Color Coding for Resistors
• Most electric circuits use circuit elements called resistors to
control the current in the various parts of the circuit.
The inverse of conductivity is resistivity, ρ:
where ρ has the units
ohm meters (ohm meters (ΩΩ m).m).

12. Color Coding for Resistors
BlackBlack
BrownBrown
RedRed
OrangeOrange
YellowYellow
GreenGreen
BlueBlue
VioledVioled
GreyGrey
WhiteWhite

13. • The first band is yellow = 4, so the first digit is 4
• The second band is violet = 7, so the second digit
is 7
• The third band is red = 2, so the multiplier is 102
• Resistor value is, R = (47 x 102
± 5%) Ω.
Color Coding for Resistors

14. Quiz
• Answer: (b)
• Answer: (b)
If voltage increases, then I is
increase exponentially,exponentially, so R
is decrease.
A = πr2
IfIf rr && ll doubled,doubled, AA increase 4x whileincrease 4x while ll onlyonly
2x, then2x, then RR is decrease.is decrease.

15. The Resistance of Nichrome Wire
Example:
The radius of 22-gauge Nichrome wire is 0.32 mm.
• (A) Calculate the resistance per unit length of
this wire.
• (B) If a potential difference of 10 V is maintained
across a 1.0-m length of the Nichrome wire,
what is the current in the wire?

16. Solution
• (A) The resistance per unit lengthThe resistance per unit length:
• (B) TThe current in the wirehe current in the wire:

17. Electrical Power
• The electric potential energy of the system decreases as the
charge Q passes through the resistor:
• Power P, representing the rate at which energy is delivered to
the resistor, is
• SI unit of power is the watt (W).

18. Quiz
• For the two lightbulbs shown in Figure 27.13, rank the
current values at points a through f from greatest to
least.
Answer:
• IIaa = I= Ibb > I> Icc = I= Idd > I> Iee = I= Iff

19. Example
Power in an Electric HeaterPower in an Electric Heater
• An electric heater is constructed by applying a potential
difference of 120 V across a Nichrome wire that has a total
resistance of 8.00 V. Find the current carried by the wire and
the power rating of the heater.
ANSWER:

20. Example
Linking Electricity and
Thermodynamics
• An immersion heater must increase the temperature of 1.50
kg of water from 10.0°C to 50.0°C in 10.0 min while operating
at 110 V.
• (A) What is the required resistance of the heater?
• (B) Estimate the cost of heating the water.

21. Solution (A)
• An immersion heater must increase the temperature of 1.50
kg of water from 10.0°C to 50.0°C in 10.0 min while operating
at 110 V.
• (A) What is the required resistance of the heater?

22. Solution (B)
• An immersion heater must increase the temperature of 1.50
kg of water from 10.0°C to 50.0°C in 10.0 min while operating
at 110 V.
• (B) Estimate the cost of heating the water.
• If price of electric energy is 11¢ per kilowatt-hour:

23. Resistors inResistors in Series & ParallelSeries & Parallel
RReqeq: Equivalent resistance: Equivalent resistance
Parallel:Parallel:
SeriesSeries
ParallelParallel

24. Quiz
Answer: (b)
II == VV//RR11 (switch closed)(switch closed)
II == VV/(/(RR11++RR22) (switch open)) (switch open)
Then,Then,
II is decrease when switch openis decrease when switch open

25. Quiz
• a
Answer: (a)
RReqeq is smaller/decrease in parallel connection,is smaller/decrease in parallel connection,
so, currentso, current II will be increaseswill be increases..

26. Quiz
Fig. 28.3Fig. 28.3 Fig. 28.5Fig. 28.5
Answer: (i) b; (ii) c; (iii) a; (iv) c

27. Example

28. Solution (B)

29. Example

30. Solution (B & C)

31. Kirchhoff’s Rules
Kirchhoff’s rules:
Currents directed into the junction are rule as +Currents directed into the junction are rule as +II,,
whereas currents directed out of a junction are -whereas currents directed out of a junction are -II..

32. Kirchhoff’s Second Rules
• Charges move from the high-potentialCharges move from the high-potential
end of a resistor toward the low-end of a resistor toward the low-
potential endpotential end, a resistor is traversed in
the direction of the current, the
potential differencepotential difference: ∆V = -IR.
• If a resistor is traversed in the direction
opposite the current: ∆V = +IR.
• If a source of emf is traversed in the
direction of the emf (from negative to
positive): ∆V = +ε.
• If a source of emf is traversed in the
direction opposite of the emf (from
positive to negative): ∆V = -ε.

33. Example: A Single-Loop Circuit

34. Example: A multiloop circuit

35. Solution