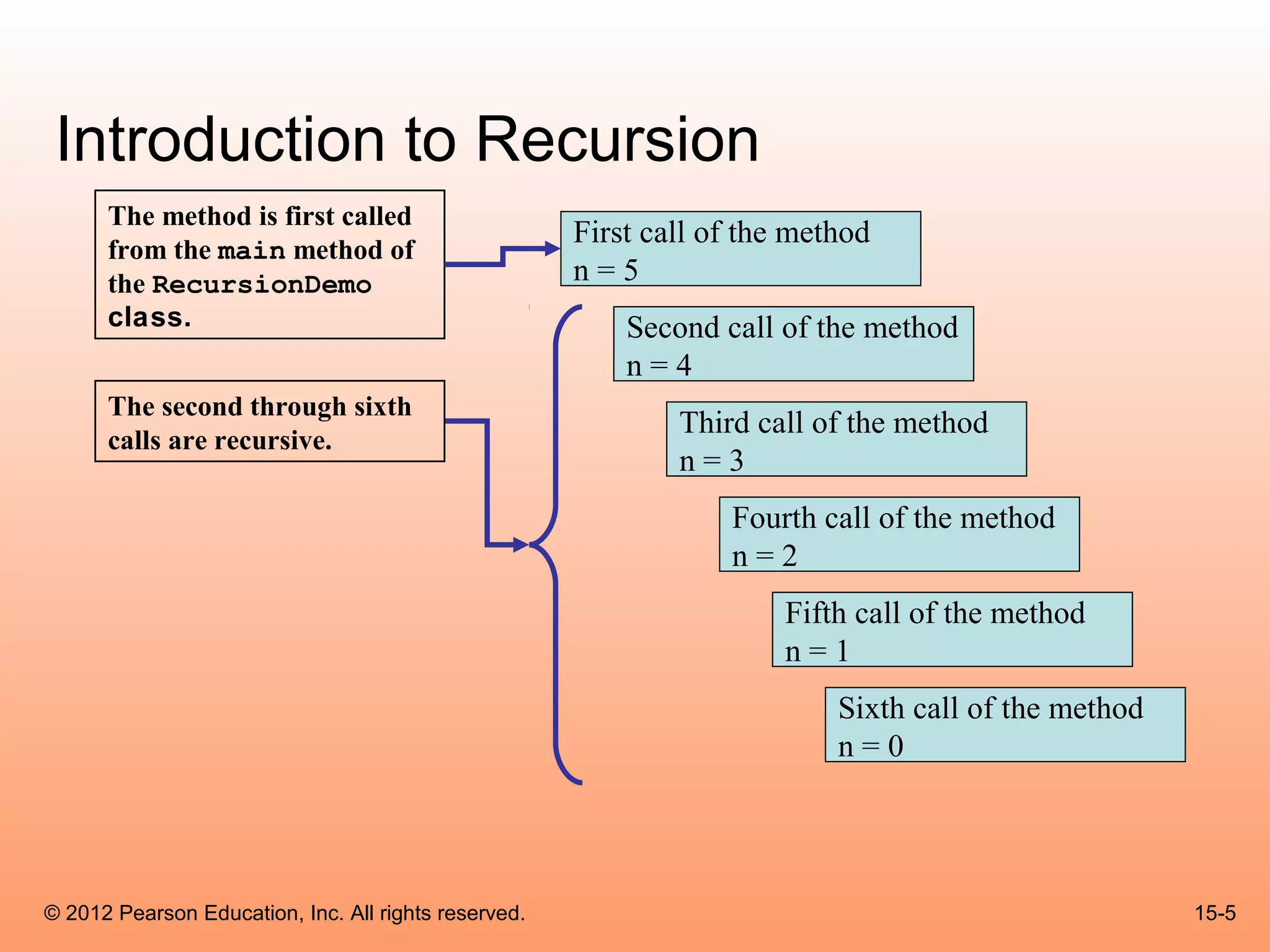
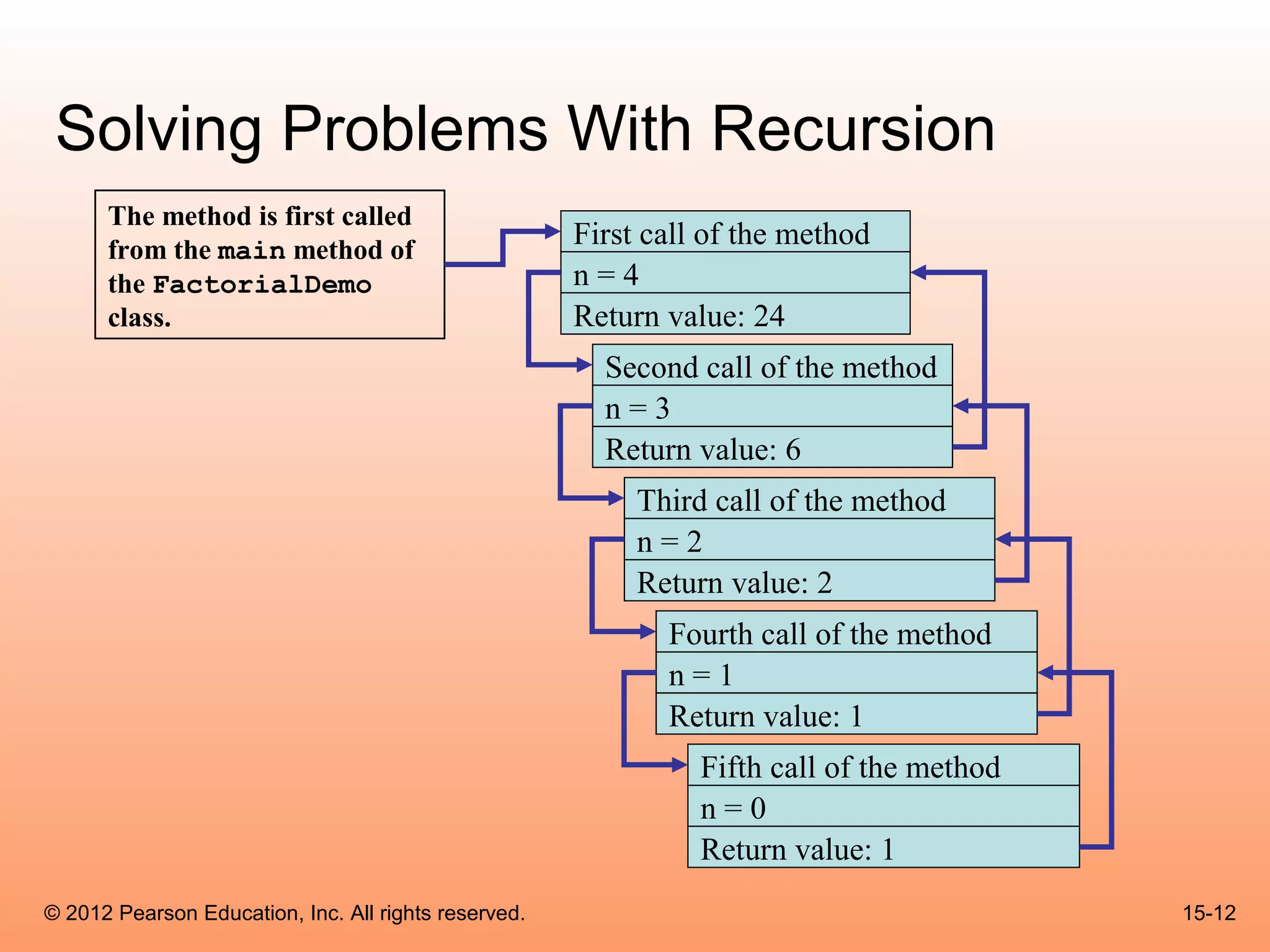
This document summarizes key topics from Chapter 15 on recursion from the textbook "Starting Out with Java: From Control Structures through Data Structures". It discusses introduction to recursion, solving problems with recursion, examples of recursive methods, and the Towers of Hanoi problem. Recursion involves a method calling itself directly or indirectly. It is used to solve repetitive problems by reducing them to smaller instances until a base case is reached. Examples demonstrated include calculating factorials and Fibonacci numbers recursively.











![Summing a Range of Array Elements
• Recursion can be used to sum a range of array elements.
• A method, rangeSum takes following arguments:
– an int array,
– an int specifying the starting element of the range, and
– an int specifying the ending element of the range.
– How it might be called:
int[] numbers = {1, 2, 3, 4, 5, 6, 7, 8, 9};
int sum;
sum = rangeSum(numbers, 3, 7);
© 2012 Pearson Education, Inc. All rights reserved. 15-14](https://image.slidesharecdn.com/csogaddisjavachapter15-130411104101-phpapp01/75/Cso-gaddis-java_chapter15-14-2048.jpg)
![Summing a Range of Array Elements
• The definition of the rangeSum method:
public static int rangeSum(int[] array,
int start, int end)
{
if (start > end)
return 0;
else
return array[start]
+ rangeSum(array, start + 1, end);
}
• Example: RangeSum.java
© 2012 Pearson Education, Inc. All rights reserved. 15-15](https://image.slidesharecdn.com/csogaddisjavachapter15-130411104101-phpapp01/75/Cso-gaddis-java_chapter15-15-2048.jpg)





