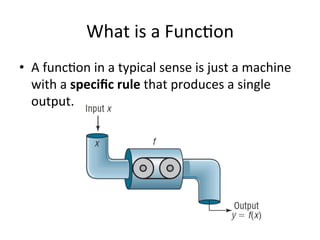
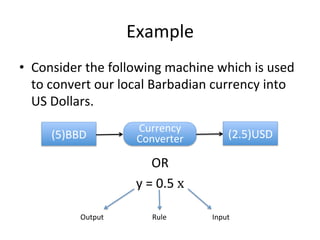
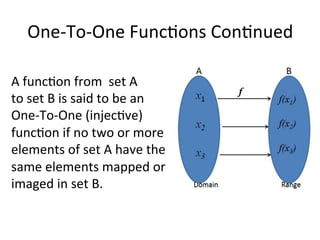
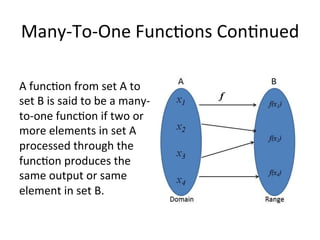
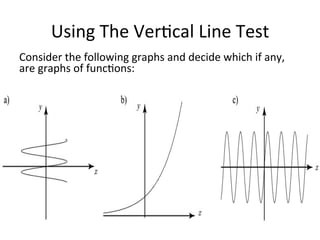
The document serves as a foundational introduction to functions and relations in pre-calculus. It explains the definitions of functions and relations, types of relations such as one-to-one and many-to-one, and methods to test for functions using examples. It also discusses notation for functions, including graphical representation and the vertical line test for verifying functions.

1. Pre-­‐Calculus
Kevin
Small
–
www.cxctutor.org
An
Introduc<on
To
Func<ons
and
Rela<ons

2. Topics
To
Be
Covered
•
Define
What
is
a
Func/on
– Show
Simple
Examples
of
Func<ons
– Explain
How
Func<on
Nota<on
Works
•
Define
What
is
a
Rela/on
– Define
The
Terms
Domain
and
Range
– Learn
How
To
Draw
Mapping
Diagrams
– Learn
The
Different
Types
of
Rela<ons
– Lean
How
To
Test
For
Func<ons

3. What
is
a
Func<on
• A
func<on
in
a
typical
sense
is
just
a
machine
with
a
specific
rule
that
produces
a
single
output.

4. Example
• Consider
the
following
machine
which
is
used
to
convert
our
local
Barbadian
currency
into
US
Dollars.
OR
y
=
0.5
x
(5)BBD
Currency
Converter
(2.5)USD
Output
Rule
Input

5. Example
Con<nued
The
func<on
given
is
an
example
of
a
Linear
Func/on.
We
will
discuss
the
graphs
of
func<ons
later
but
here
is
the
graph
of
our
currency
converter
func<on.

6. Func<on
Nota<on
• There
is
a
more
appropriate
way
that
we
use
in
calculus
to
represent
a
func<on
in
wri<ng
and
that
is:
f(x) = y
The
input
(variable)
is
listed
in
brackets
Output
Name
of
Func<on

7. Func<on
Nota<on
Examples
Example:
•
f(x)
=
x
+
1
• A(r)
=
πr2
• V(h,r)
=
πr2h

8. Rela<ons
The
topic
of
func<ons
is
in
fact
in
sub-­‐topic
under
him
much
broader
subject
In
mathema<cs
called
Rela/ons.
Defini<on:
A
rela<on
is
a
set
of
ordered
pairs.
What
it
is
an
ordered
pair?
Well
let
us
use
this
func<on
as
an
example:
f(x) = x2 + 1

9. Let
us
list
our
inputs
from
1
to
5
and
calculate
their
corresponding
outputs:
Now
we
can
pair
our
inputs
with
our
outputs
in
an
orderly
fashion
like
this:

10. Formal
Defini<on
of
a
Func<on
• A
func<on
a
special
rela<on
in
which
each
element
x
in
the
Domain
is
paired
using
a
rule,
with
exactly
one
and
only
one
element
f(x)
in
the
Range.
• There
are
two
types
of
rela<ons
that
sa<sfy
this
criteria
and
they
are
called
one-­‐to-­‐one
and
many-­‐to-­‐one
rela<ons.
• A
one-­‐to-­‐many
rela<on
is
NOT
a
func<on.

11. Example
of
One-­‐To-­‐One
Func<on
Consider
the
rela<on
f:
x
→
2x
+
5
given
that
the
domain
is
Find
the
corresponding
range
values
and
hence
draw
a
mapping
diagram
to
represent
the
rela<on.
0,
1,
2,
3

12. One-­‐To-­‐One
Func<ons
Con<nued
A
func<on
from
set
A
to
set
B
is
said
to
be
an
One-­‐To-­‐One
(injec<ve)
func<on
if
no
two
or
more
elements
of
set
A
have
the
same
elements
mapped
or
imaged
in
set
B.

13. Many-­‐To-­‐One
Func<ons
Consider
the
func<on
f(x)
=
x2
and
let
our
domain
be
{-­‐2 ≤ x ≤ 2}.

14. Many-­‐To-­‐One
Func<ons
Con<nued
A
func<on
from
set
A
to
set
B
is
said
to
be
a
many-­‐
to-­‐one
func<on
if
two
or
more
elements
in
set
A
processed
through
the
func<on
produces
the
same
output
or
same
element
in
set
B.

15. One-­‐To-­‐Many
is
Not
A
Func<on
Consider
the
inverse
of
func<on
f(x)
=
x2
in
which
we
generate
by
exchanging
the
values
for
the
domain
and
range.
The
inverse
func<on
follows
the
rule:
f
’(x)
=
±
√x

16. A
Visual
Test
For
Func<ons
We
can
use
a
very
simple
test
called
the
Ver/cal
Line
Test
to
determine
whether
the
Graph
of
A
Rela/on
in
indeed
a
func<on
or
not.
• Defini<on:
– Given
a
curve
drawn
in
the
coordinate
plane.
Then
this
curve
is
a
graph
of
a
func<on
if
and
only
if
no
ver<cal
line
can
be
made
to
intersect
the
curve
at
more
than
one
point.

17. Using
The
Ver<cal
Line
Test
Consider
the
following
graphs
and
decide
which
if
any,
are
graphs
of
func<ons: