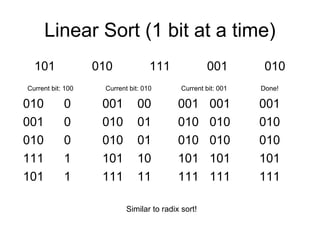
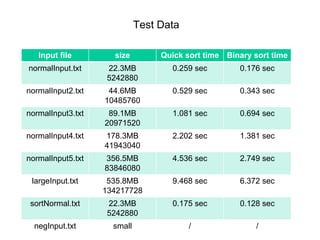
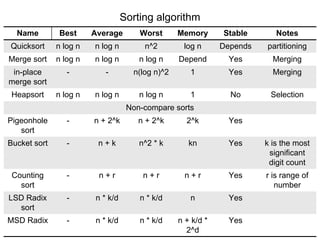
This document describes the binary sort algorithm, a non-comparison sorting algorithm that sorts data by examining bits of information one bit at a time from most significant to least significant. It has a time complexity of O(kn) where k is the number of bits in each data item and n is the number of items. The algorithm works by recursively sorting subsets of the data based on the value of each bit, placing 0s in one group and 1s in another. It is an in-place, linear sorting algorithm.

1. CS 375
Final Project
Liyu Ying

2. Binary Sort Algorithm
• Binary code only has 0/1
– Lower number complexity
– 1: true 0: false
– All data are 0/1 (machine language)
• Using binary code to sort data
– It is a linear sort
– It is a non-compare sort
– It is an in place sort
– Not a stable sort (It can be)

3. Binary Sort algorithm
• A number has a higher rank if it has a
larger value
• A number with a higher rank is greater
than sum of its lower rank
>
This can be proved by induction

4. Induction
• Base case: n = 0
• 2 > 1
• Induction step
Assume that > is true for some
k >= n, to show >
+ > +

5. Pseudocode
binarySort (leftIndex, rightIndex, currentBit)
int I = leftIndex, j = rightIndex
while (i <= j) {
//find first data with value 0 at currentBit, starting from left
while (data[i] & currentBit)
i++;
//find first data with value 1 at currentBit, starting from right
while (!(data[j] & currentBit))
j--;
if (i < j) {
swap data[i] and data[j]
}
}
nextBit = currentBit >> 1;
if (nextBit) {
binarySort(LeftIndex, i - 1, nextBit);
binarySort(j, rightIndex, nextBit)
}

6. Linear Sort (1 bit at a time)
101 010 111 001 010
Current bit: 010
001 00
010 01
010 01
101 10
111 11
Current bit: 100
010 0
001 0
010 0
111 1
101 1
Current bit: 001
001 001
010 010
010 010
101 101
111 111
Done!
001
010
010
101
111
Similar to radix sort!

7. Non-compare sort
• Does not read the value of data, take 1/0
as true/false.
• Does not care about the value between
data

8. In place sort
• Divide and conquer
• Space complexity:
– O(1)
• Does not require extra information
• Might be faster to copy a new array => O(2)

9. Time complexity
• O(1) to read one data
• O(k) to read one bit value.
– Depending on data type k = 16/32/64…
• O(n) to read one data set has n data
Total time: O(kn)
If the hardware supports reading one bit at one time:
O(1) to read one bit
O(k) to read one data (which cost the same time as O(1))
O(n) to read one data set has n data
Total time: O(n)

10. Test Data
Input file size Quick sort time Binary sort time
normalInput.txt 22.3MB
5242880
0.259 sec 0.176 sec
normalInput2.txt 44.6MB
10485760
0.529 sec 0.343 sec
normalInput3.txt 89.1MB
20971520
1.081 sec 0.694 sec
normalInput4.txt 178.3MB
41943040
2.202 sec 1.381 sec
normalInput5.txt 356.5MB
83846080
4.536 sec 2.749 sec
largeInput.txt 535.8MB
134217728
9.468 sec 6.372 sec
sortNormal.txt 22.3MB
5242880
0.175 sec 0.128 sec
negInput.txt small / /

12. Name Best Average Worst Memory Stable Notes
Quicksort n log n n log n n^2 log n Depends partitioning
Merge sort n log n n log n n log n Depend Yes Merging
in-place
merge sort
- - n(log n)^2 1 Yes Merging
Heapsort n log n n log n n log n 1 No Selection
Non-compare sorts
Pigeonhole
sort
- n + 2^k n + 2^k 2^k Yes
Bucket sort - n + k n^2 * k kn Yes k is the most
significant
digit count
Counting
sort
- n + r n + r n + r Yes r is range of
number
LSD Radix
sort
- n * k/d n * k/d n Yes
MSD Radix - n * k/d n * k/d n + k/d *
2^d
Yes
Sorting algorithm

13. Limitations
• Negative numbers:
– The sorted order of negative numbers is
reversed
• Data type:
– Double/float… these types do not support
binary shift and logical and because of how
they are encoded. But the algorithm can also
work for these if you can
• Sort by exponent first
• Sort by base

14. Example
• Find a function to find the exponent and base bits
– Double:
• O(exponent) + O(base) = O(11n) + O(53n) = O(64n)
• The exponent and base follow the binary sort algorithm
– By induction:
>

15. Example with Negative #’s
-1 -5 -3 4 7
4 00100
7 00111
-5 11011
-3 11101
-1 11111
Result:
As you can see, the negative numbers are
sorted in reverse order.

16. Searching and Inserting
- We can consider the sort algorithm as a tree structure
- The parent is the current interval of data that we will
sort
- The left child contains all 0 values at the current bit
- The right child contains all 1 values at the current bit
- The parent is a combination of its children

17. 00
01
10
11
00
01
10
11
00 01 10 11
[0,3
]
[0,1
]
[2,3
]
[0,0
]
[1,1
]
[2,2
]
[3,3
]
00 01 10 11
Index Interval Values at Index
Example of Tree Structure
- To insert/search 2 (which is 10)
Look at node ((2*1 + 1)*2 + 0) = 6
- To insert/search 1 (which is 01)
Look at node ((2*1 + 0)*2 + 1) = 5
Node 1Node 1
Node 3Node 2
Node 4 Node 5 Node 6 Node 7
- Time complexity: O(1)
- Constant!

18. What is interesting?
• The whole sort can be done in hardware!
– No mean to calculate time complexity anymore.
Sorting huge data will be done much more faster.
– SSD already provide a direct address access by
NAND flash and cells. If we can read one cell at one
time…?
– Cloud computing:
• Double the computing speed each time divide the data
• Larger data, faster computing
• The algorithm can sort all data type:
– Providing math function
– Extra information such as ASCII table