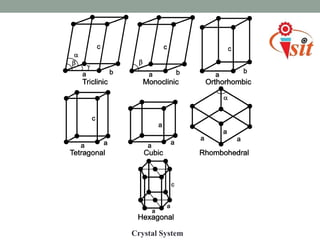
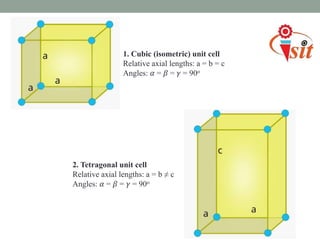
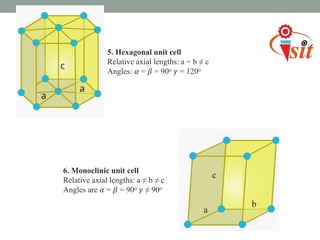
There are 7 crystal systems based on the symmetry and shape of the unit cell: 1. Cubic system has equal lattice parameters and 90 degree angles. 2. Tetragonal system has equal a and b parameters and 90 degree angles. 3. Orthorhombic system has unequal parameters and 90 degree angles. 4. Rhombohedral system has equal parameters and non-90 degree angles. 5. Hexagonal system has equal a and b parameters, non-equal c, and 90 and 120 degree angles. 6. Monoclinic system has unequal parameters and one 90 degree angle. 7. Triclinic system has unequal parameters and no 90 degree angles.

1. CRYSTAL
SYSTEM
Mr. Vikram B. Nalawade
vbnalawade@sitcoe.og.in
Assistant Professor,
Mechatronics Engineering Department,
Sharad Institute of Technology College of Engineering, Yadrav -
Ichalkaranji

2. Index
• Lattice
• Basis
• Crystal Structure
• Unit Cell
• Crystal System
Crystal Structure = Lattice + Basis

3. Basics of Crystal Structure
• A crystalline material is one in which the atoms are situated in a
repeating or periodic array over large atomic distances—that is,
long-range order exists, such that upon solidification, the atoms
will position themselves in a repetitive three-dimensional
pattern, in which each atom is bonded to its nearest neighbor
atoms.
• All metals, many ceramic materials, and certain polymers form
crystalline structures under normal solidification conditions.
• For those that do not crystallize, this long-range atomic order is
absent; these non-crystalline or amorphous materials .

4. For the face-centered cubic crystal structure, (a) a hard-sphere unit cell representation, (b)
a reduced sphere unit cell, and (c) an aggregate of many atoms.

5. • Lattice-
A three-dimensional array of points coinciding with
atom positions (or sphere centers).
• Unit Cells-
The atomic order in crystalline solids indicates that
small groups of atoms form a repetitive pattern. Thus, in
describing crystal structures, it is often convenient to
subdivide the structure into small repeat entities called
unit cells.

6. Crystal Lattice and Unit Cells

7. Crystal System

8. 1. Cubic (isometric) unit cell
Relative axial lengths: a = b = c
Angles: 𝛼 = 𝛽 = 𝛾 = 90o
2. Tetragonal unit cell
Relative axial lengths: a = b ≠ c
Angles: 𝛼 = 𝛽 = 𝛾 = 90o

9. 3. Orthorhombic unit cell
Relative axial lengths: a ≠ b ≠ c
Angles: 𝛼 = 𝛽 = 𝛾 = 90o
4. Rhombohedral (trigonal) unit cell
Relative axial lengths: a = b = c
Angles: 𝛼 = 𝛽 = 𝛾 ≠ 90o

10. 5. Hexagonal unit cell
Relative axial lengths: a = b ≠ c
Angles: 𝛼 = 𝛽 = 90o 𝛾 = 120o
6. Monoclinic unit cell
Relative axial lengths: a ≠ b ≠ c
Angles are 𝛼 = 𝛽 = 90o 𝛾 ≠ 90o

11. 7. Triclinic unit cell
Relative axial lengths: a ≠ b ≠ c
Angles: 𝛼 ≠ 𝛽 ≠ 𝛾 ≠ 90o

12. Crystal System