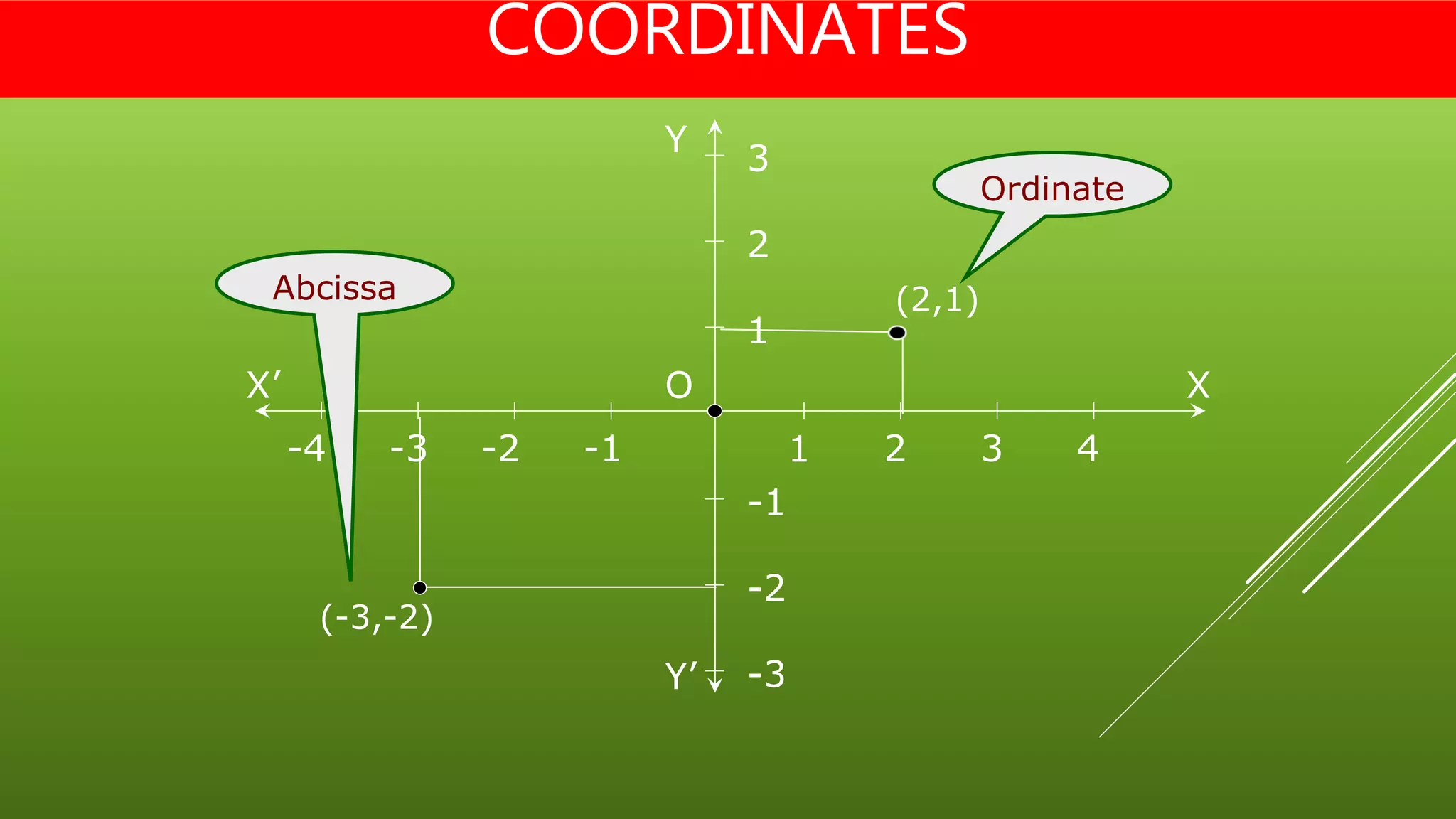
This document provides information about coordinate geometry including: 1. It introduces the Cartesian coordinate system with four quadrants defined by the x and y axes, and provides examples of coordinate points. 2. It defines the distance formula used to calculate the distance between two points in the plane using their x and y coordinates. 3. It explains the section formula, which gives the ratio between the distances of a point from two lines, and can be used to determine if three points are collinear.

1. NARAYANA E- TECHNO SCHOOL,
MADANANDAPURAM
Narayana E – Techno School, Madanandapuram
Coordinate Geomentry
S. Yuvan Pramesh
VIII Wordsworth

2. SESSION OBJECTIVES
1.Introduction
2.Cartesian Coordinate system and
Quadrants
3.Distance formula
4.Section formula
5.Collinearity of three points

5. HORIZONTAL NUMBER LINE

6. VERTICAL NUMBER LINE

7. COORDINATE AXES

8. COORDINATE SYSTEM

10. COORDINATES
XX’
Y
Y’
O
1 2 3 4-1-2-3-4
-1
-2
-3
1
2
3
(2,1)
(-3,-2)
Ordinate
Abcissa

11. QUADRANTS
Q : (1,0) lies in which Quadrant?.
XX’ O
Y
Y’
III
III IV
(+,+)(-,+)
(-,-) (+,-)
Ist? IInd?
A: None. Points which lie on the axes do not lie in any quadrant.

12. Distance Formula
x1
XX’
Y’
O
Y
x2
y1
y2
N
y2-y1
(x2-x1)
PQN is a right angled
 PQ2 = PN2 + QN2
 PQ2 = (x2-x1)2+(y2-y1)2
   2 2
2 1 2 1PQ x x y y    

13. Distance From Origin
Distance of P(x, y) from the origin is
      
2 2
OP x 0 y 0
 2 2
OP x y

14. SECTION FORMULA
L N M
H
K
XX’
Y’
O
Y Clearly AHP ~ PKB
  
AP AH PH
BP PK BK
 
  
 
1 1
2 2
x x y ym
n x x y y
2 1 2 1mx nx my ny
P ,
m n m n
  
     

15. MIDPOINT FORMULA
If P(x,y) is a Midpoint of A(x1, y1) and B(x2,y2)
AP=PB
m:n  1:1
  
   
 
1 2 1 2x x y y
P ,
2 2

17. A
B
C

18. COLLINEARITY - EXAMPLE