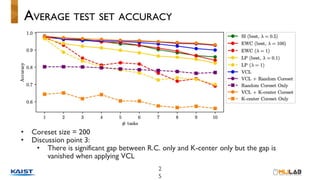
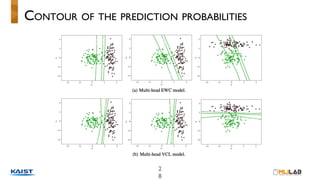
This document discusses variational continual learning for deep discriminative models. It covers continual learning backgrounds, variational inference for continual learning, the variational continual learning algorithm using a coreset, experiments comparing it to related methods, and discussion points. The variational continual learning algorithm uses a coreset to balance plasticity and stability when learning new tasks incrementally while avoiding catastrophic forgetting of old tasks. Experiments show it outperforms regularization-based methods on split MNIST and analyses the effect of coreset size and predictive uncertainty.

1. VARIATIONAL CONTINUAL LEARNING
FOR DEEP DISCRIMINATIVE MODELS
2019. 2. 27.
Wonjun Chung
wonjunc@mli.kaist.ac.kr

2. CONTENTS
1. Continual Learning Backgrounds
2. Continual Learning by Approximate Bayesian
Inference
3. Variational Continual Learning and Episodic
Memory Enhancement
4. Experiments
5. Discussion

3. PART 1
CONTINUAL LEARNING BACKGROUNDS
- CONCEPTS, BENCHMARKS

4. 4
• Continual Learning is a very general form of online learning
• Data continuously arrive in a non i.i.d way
• Tasks may change over time
• Entirely new tasks can emerge
• Model must adapt to perform well on the entire set of tasks in an
incremental way that avoids revisiting all previous data
CONCEPTS OF THE CONTINUAL LEARNING

5. 5
• It is challenging to balance between adapting to recent task and retaining
knowledge from old tasks
• Plasticity & Stability trade-off
CONCEPTS OF THE CONTINUAL LEARNING

6. 6
• Permuted MNIST
• Split MNIST/CIFAR
BENCHMARKS OF THE CONTINUAL LEARNING
Task 1
Task 2
Task 3
1 2 3

7. 7
• Split MNIST/CIFAR is more difficult than the Permuted MNIST
• Multi-head discriminative network
• Each task t has own “head network” and it is not optimization variable in
later tasks
• Discussion point 1:
• How to reduce catastrophic forgetting in the multi-head networks?
BENCHMARKS OF THE CONTINUAL LEARNING

8. PART 2
CONTINUAL LEARNING BY
APPROXIMATE BAYESIAN INFERENCE
- VARIATIONAL INFERENCE

9. 9
• Bayesian Inference provides a natural framework for continual learning
BAYESIAN INFERENCE IN CONTINUAL LEARNING
.
.
.

10. 1
0
• The posterior distribution after seeing T tasks(datasets) is recovered by
applying Bayes’ rule:
• True posterior distribution is intractable
• Approximation is required
• Variational KL minimization (Variational Inference)
BAYESIAN INFERENCE IN CONTINUAL LEARNING

11. 1
1
• Recall
VARIATIONAL INFERENCE
Variational Lower Bound (Appendix)

12. PART 3
VARIATIONAL CONTINUAL LEARNING AND EPISODIC
MEMORY ENHANCEMENT
- CORESET ALGORITHM

13. 1
3
VARIATIONAL CONTINUAL LEARNING
Goal of VCL
: Set of allowed approximate posteriors (Gaussian mean-field approx.)
: Intractable normalizing constant (not required)
• Zeroth approximate distribution is defined to be the prior :
• Repeated approximation may accumulate errors causing the model to forget old
tasks.
• Gaussian mean-field approximation :

14. 1
4
• For each task, is produced by selecting new data points from the current task and a
selection from the old corset
• Any heuristic can be used to make selections
• Random, K-Center algorithm
CORESET
Coreset
: Small representative set of data from previously observed data in order to mitigate
catastrophic forgetting

15. 1
5
• Input: Prior
• Output:
• Initialize the coreset and variational approximation:
• For 1st task (t = 1),
• Observe the dataset
• update the coreset using and
• Update the variational distribution for non-coreset data points:
CORESET VCL ALGORITHM

16. 1
6
• Con’t
• Compute the final variational distribution:
• Only used for prediction, and not propagation
• Perform prediction at test input :
• Iterate for t = 1… T
CORESET VCL ALGORITHM

17. 1
7
CORESET VCL ALGORITHM
Train
Test
• Discussion point 2 : Is it reasonable?

18. 1
8
• Recall
OBJECTIVE OF VCL
Final objective
minimizing with respect to the variational parameter
Regularization Likelihood

19. 1
9
• KL divergence of between two Gaussian can be computed in closed-form (Appendix)
• Expected log likelihood requires further approximation
• Monte Carlo Sampling
• Local Reparameterization trick
•
•
OBJECTIVE OF VCL
Final objective
minimizing with respect to the variational parameter

20. 2
0
•
MONTE CARLO GRADIENTS
Proposition
Let be a random variable having a probability density given by and let
where is a deterministic function. Suppose further that the marginal probability
density of is such that
Then a function with derivatives in :

21. PART 4
EXPERIMENTS
- OVERVIEW OF RELATED WORKS, CONTRAST

22. 2
2
• Continual Learning for Deep Discriminative models:
• Regularized maximum likelihood estimation
RELATED WORK
Regularization termLikelihood
: Overall regularization strength
: Diagonal matrix that encodes the relative strength of regularization on each element of

23. 2
3
• Continual Learning for Deep Discriminative models:
• Regularized maximum likelihood estimation
• Laplace Propagation (LP) : Laplace’s approximation at each step
• Diagonal Laplace propagation
RELATED WORK
Penalty termLikelihood
: Initialized using the covariance of the Gaussian prior

24. 2
4
• Elastic Weight Consolidation(EWC) :
• Approximating the average Hessian of the likelihoods using the Fisher information
• Regularization:
• Synaptic Intelligence (SI):
: Comparing the changing rate of the gradients of the objective and the changing
rate of the parameters
RELATED WORK
Only for just before task :
All previous tasks :

25. 2
5
• Permuted MNIST
• Coreset size = 200
• Discussion point 3:
• There is significant gap between R.C. only and K-center only but the gap is
vanished when applying VCL
AVERAGE TEST SET ACCURACY

26. 2
6
• There is no significant performance gap between VCL w.o coreset and large Coreset
EFFECT OF CORESET SIZE

27. 2
7
• VCL outperforms EWC and LP but it is slightly worse than SI.
SPLIT MNIST ACCURACY

28. 2
8
CONTOUR OF THE PREDICTION PROBABILITIES

29. PART 5
DISCUSSION

30. 3
0
• Discussion point 1:
• How to reduce catastrophic forgetting in the multi-head networks?
• Discussion point 2 :
• Is it reasonable?
• Discussion point 3:
• There is significant gap between R.C. only and K-center only but the gap is
vanished when applying VCL
• They use Bayesian Neural Networks but did not mention about uncertainty.
• How does learning new task affect uncertainty of the old model?
• Uncertainty-Guided Continual Learning?
DISCUSSION

31. ANY QUESTIONS?

32. 32
• Variational Continual Learning (ICLR 2018)
• Weight Uncertainty in Neural Networks (ICML 2015)
REFERENCES

33. 33
APPENDIX
• KL divergence of two Gaussians:
where,

34. 34
• con’t
APPENDIX