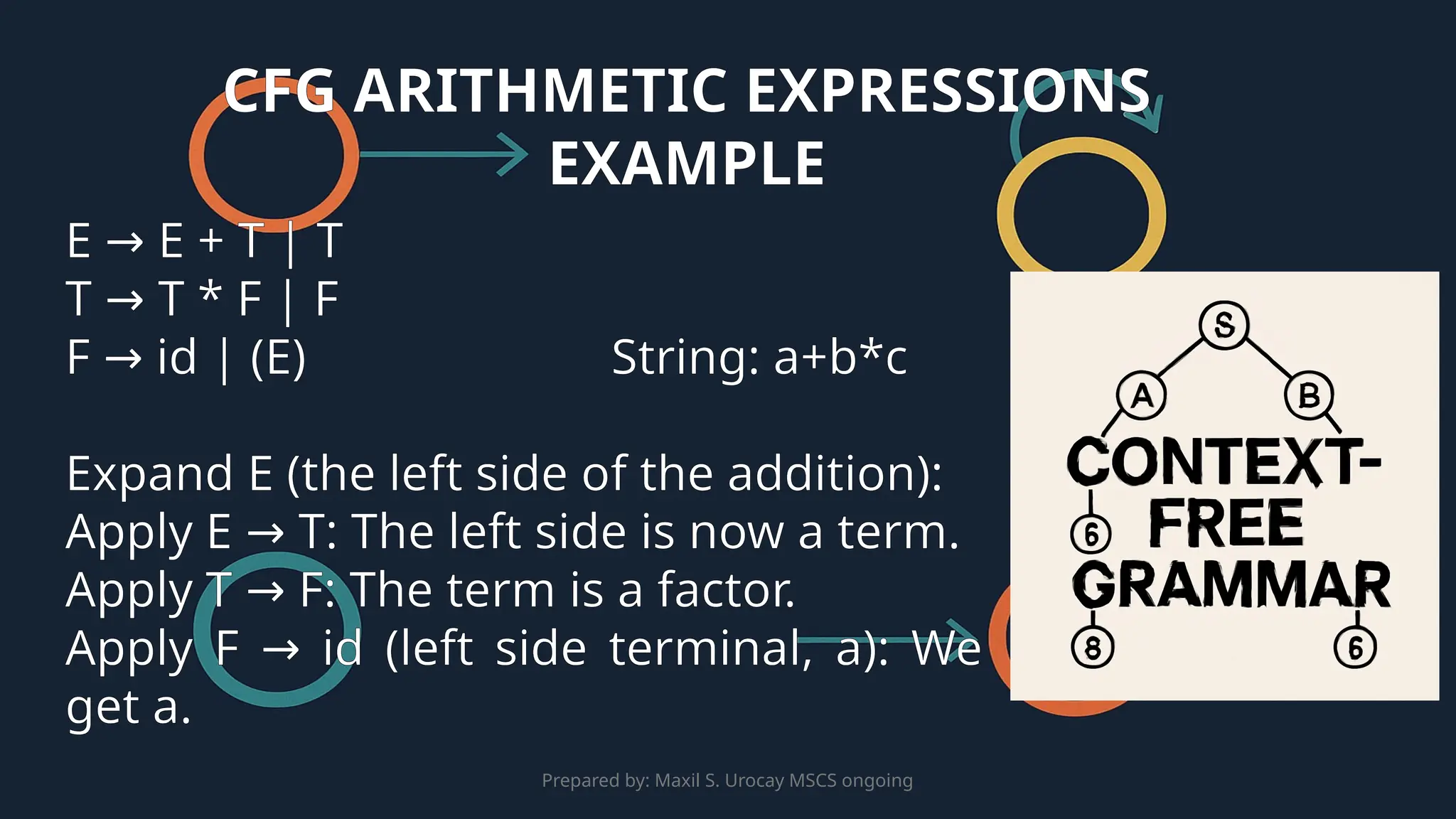
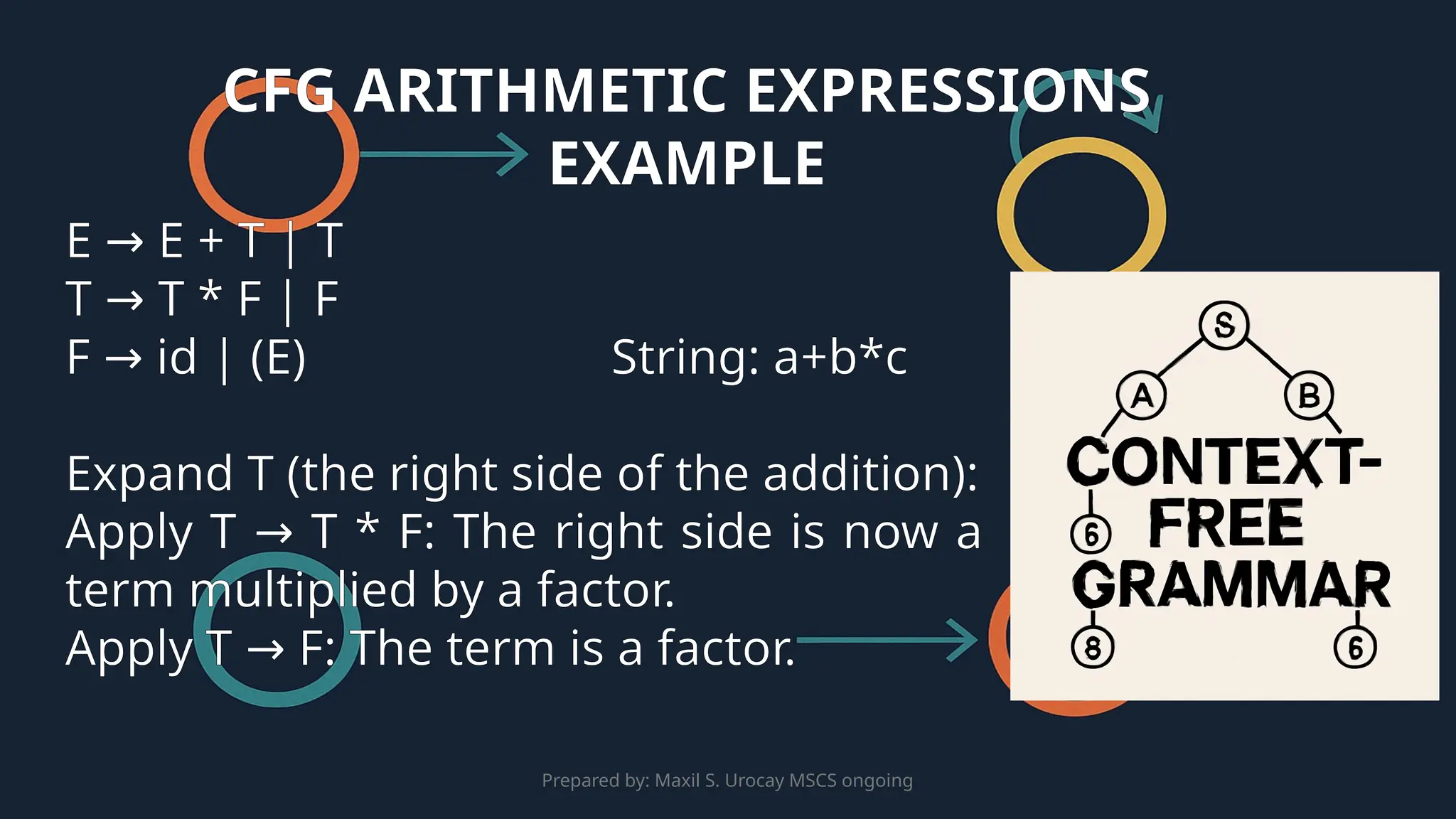
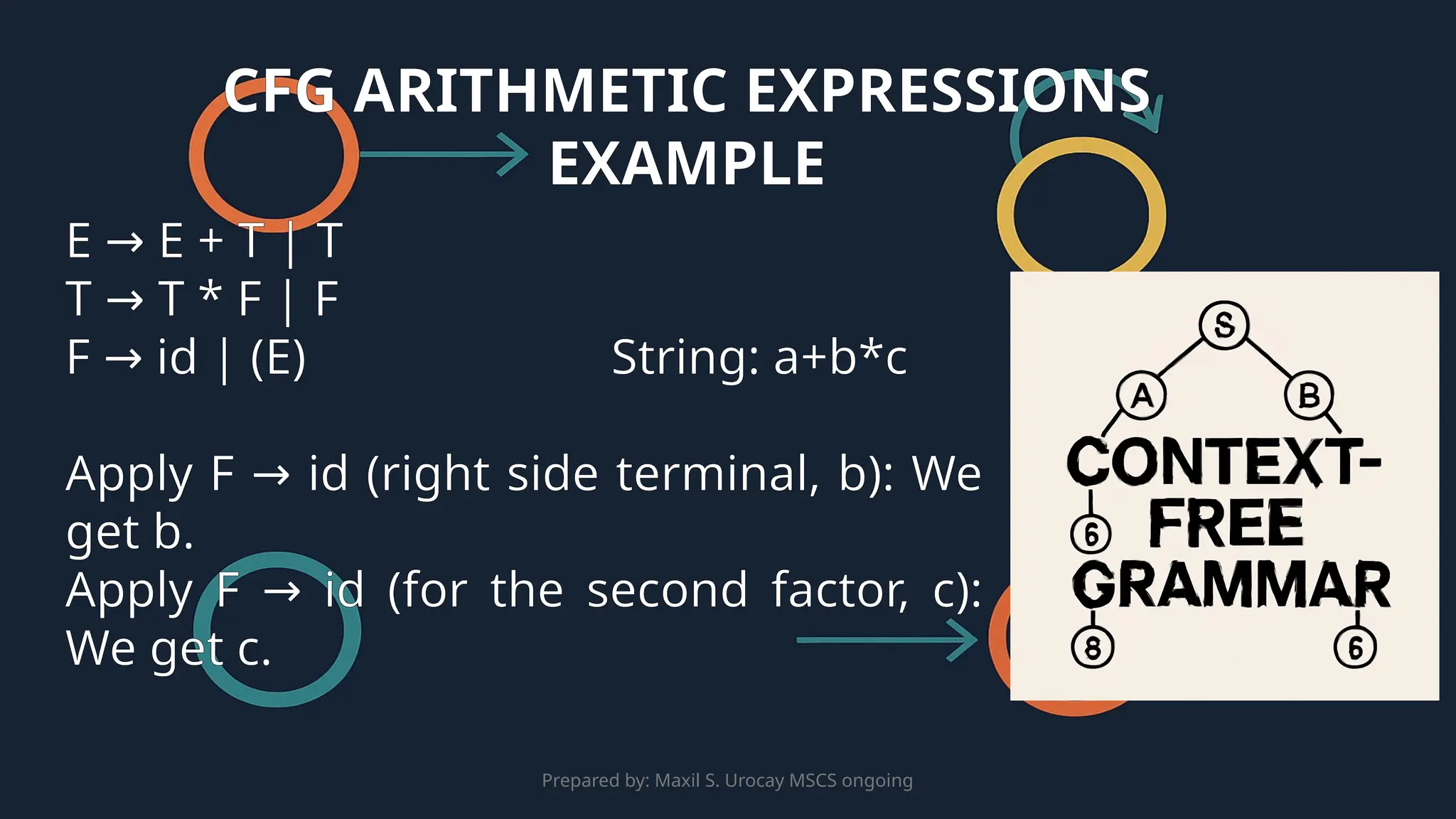
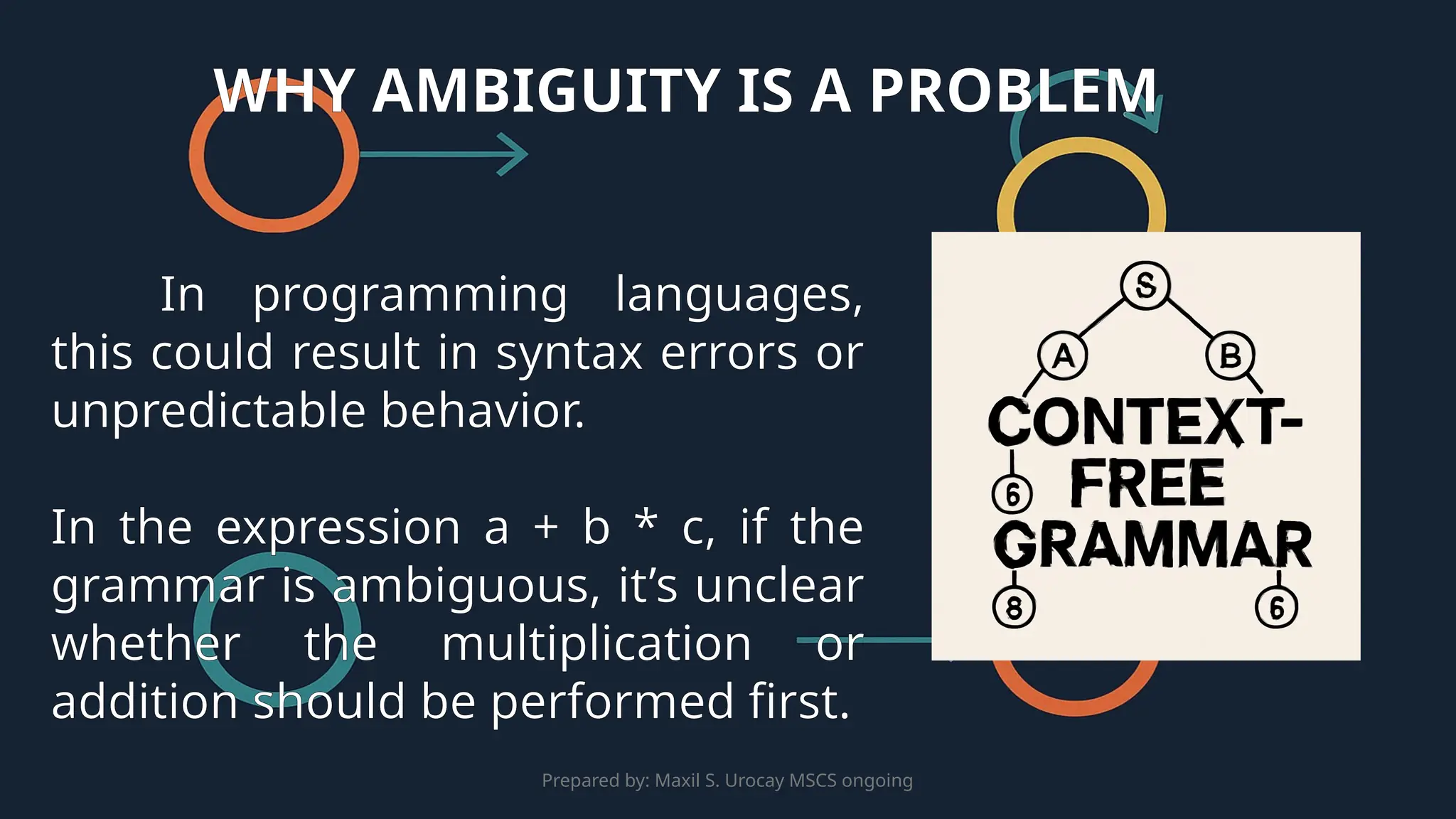
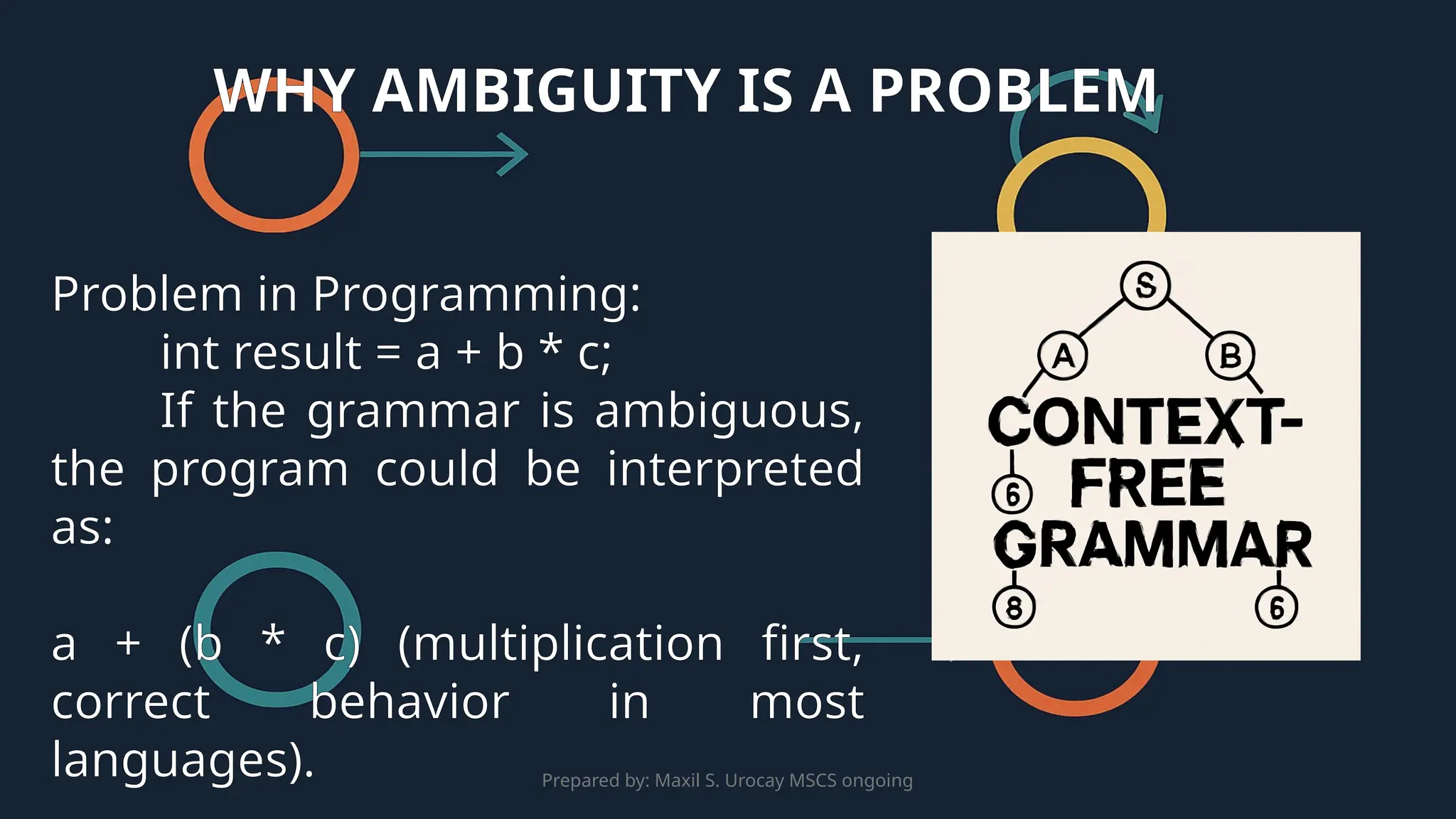
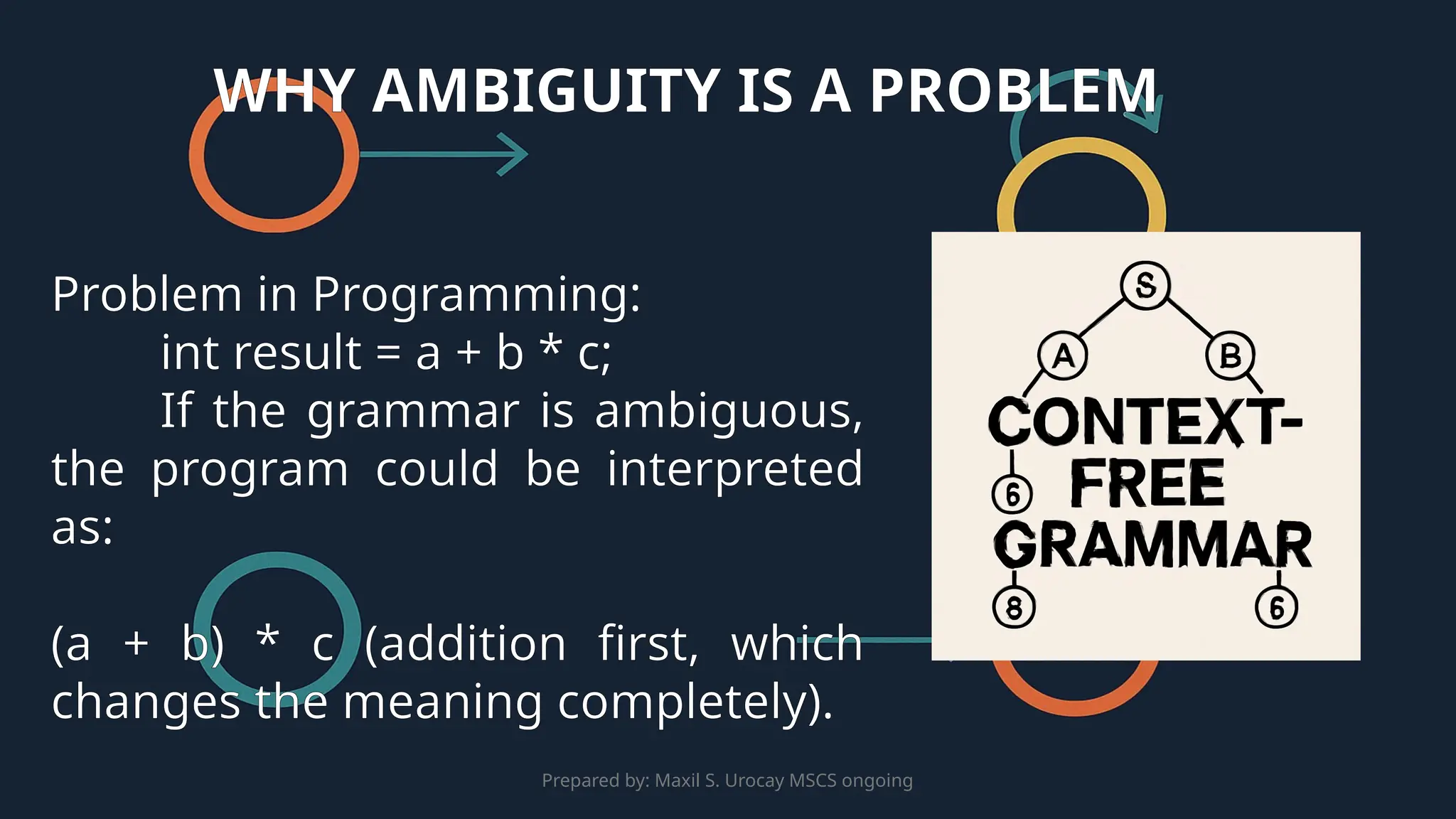
This presentation introduces Context-Free Grammars (CFGs) and their applications in language processing. It explains the components of CFGs, such as non-terminals, terminals, production rules, and the start symbol, and how they generate strings in a language. The presentation explores CFGs in programming language design, Natural Language Processing (NLP), and parsing techniques. Additionally, it covers the importance of parse trees, derivations, and the challenges of ambiguity in grammars, emphasizing how parse trees are used in compilers, machine translation, and language models.