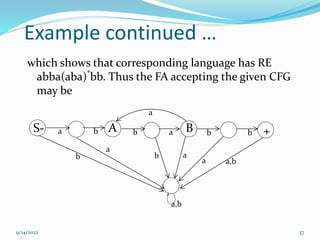
The document discusses context-free grammars (CFGs) and provides examples to illustrate various concepts: - Terminals are symbols that cannot be replaced, while non-terminals must be replaced. Productions are grammatical rules. - A CFG consists of an alphabet of terminals, non-terminals including a start symbol S, and productions replacing non-terminals with strings of terminals/non-terminals. - Several examples of CFGs are given that generate languages like a*, (a+b)*, and anbn showing how words are derived through productions.

1. Shumaila Shoukat

2. 2
Terminals: The symbols that can’t be replaced by
anything are called terminals.
Non-Terminals: The symbols that must be replaced
by other things are called non-terminals.
Productions: The grammatical rules are often called
productions.
CFG terminologies
9/14/2022

3. 3
CFG
CFG is a collection of the followings
1. An alphabet  of letters called terminals from
which the strings are formed, that will be the
words of the language.
2. A set of symbols called non-terminals, one of
which is S, stands for “start here”.
3. A finite set of productions of the form
non-terminal  finite string of terminals and
/or non-terminals.
Following is a note in this regard
9/14/2022

4. 4
Note
The terminals are designated by small letters, while
the non-terminals are designated by capital letters.
There is at least one production that has the non-
terminal S as its left side.
9/14/2022

5. 5
Context Free Language (CFL)
The language generated by CFG is called
Context Free Language (CFL).
Example:
 = {a}
productions:
1. S aS
2. SΛ
Applying production (1) six times and then
production (2) once, the word aaaaaa is
generated as
9/14/2022

6. 6
S aS
aaS
aaaS
aaaaS
aaaaaS
aaaaaaS
aaaaaaΛ
= aaaaaa







9/14/2022

7. 7
Example continued …
It can be observed that prod (2) generates
Λ, a can be generated applying prod. (1)
once and then prod. (2), aa can be
generated applying prod. (1) twice and
then prod. (2) and so on. This shows that
the grammar defines the language
expressed by a*
.
9/14/2022

8. 8
Example
 = {a}
productions:
1. SSS
2. Sa
3. SΛ
This grammar also defines the language
expressed by a*
.
Note: It is to be noted that Λ is considered to be
non-terminal. It has a special status. If for a
certain non-terminal N, there may be a
production NΛ. This simply means that N can
be deleted when it comes in the working string.
9/14/2022

9. 9
Example
 = {a,b}
productions:
1. SX
2. SY
3. XΛ
4. YaY
5. YbY
6. Ya
7. Yb
9/14/2022

10. 10
Example continued …
All words of this language are of either X-type
or of Y-type. i.e. while generating a word the
first production used is SX or SY. The
words of X-type give only Λ, while the words of
Y-type are words of finite strings of a’s or b’s or
both i.e. (a+b)+
. Thus the language defined is
expressed by (a+b)*
.
9/14/2022

11. 11
Example
 = {a,b}
productions:
1. SaS
2. SbS
3. Sa
4. Sb
5. SΛ
This grammar also defines the language
expressed by (a+b)*
.
9/14/2022

12. 12
Example
 = {a,b}
productions:
1. SXaaX
2. XaX
3. XbX
4. XΛ
This grammar defines the language expressed
by (a+b)*
aa(a+b)*
.
9/14/2022

13. Example
 = {a,b}
productions:
1. S → SS
2. S → XS
3. S → Λ
4. S → YSY
5. X → aa
6. X → bb
7. Y → ab
8. Y → ba
This grammar generates EVEN-EVEN language.
9/14/2022 13

14. Example
 = {a,b}
productions:
1. S → aB
2. S → bA
3. A → a
4. A → aS
5. A → bAA
6. B → b
7. B → bS
8. B → aBB
This grammar generates the language EQUAL(The
language of strings, with number of a’s equal to number
of b’s).
9/14/2022 14

15. Note
It is to be noted that if the same non-terminal
have more than one productions, it can be
written in single line e.g.
S → aS, S → bS, S → Λ can be written as
S → aS|bS|Λ
It may also be noted that the productions
S → SS|Λ always defines the language which
is closed w.r.t. concatenation i.e.the language
expressed by RE of type r*
. It may also be
noted that the production S → SS defines
the language expressed by r+
.
9/14/2022 15

16. Example
Consider the following CFG  = {a,b}
productions:
1. S → YXY
2. Y → aY|bY|Λ
3. X → bbb
It can be observed that, using prod.2, Y generates
Λ. Y generates a. Y generates b. Y also generates
all the combinations of a and b. thus Y generates
the strings generated by (a+b)*
. It may also be
observed that the above CFG generates the
language expressed by (a+b)*
bbb(a+b)*
.
Following are four words generated by the given
CFG
9/14/2022 16

17. Example continued …
S → YXY
→ aYbbbΛ
→ abYbbb
→ abΛbbb
= abbbb
S → YXY
→ ΛbbbaY
→ bbbabY
→
bbbabaY
→
S → YXY
→ bYbbbaY
→ bΛbbbabY
→ bbbbabbY
→ bbbbabbaY
→ bbbbabbaΛ
= bbbbabba
S → YXY
→
bYbbbaY
→
9/14/2022 17

18. Example
Consider the following CFG
1. S → SS|XaXaX|Λ
2. X → bX|Λ
It can be observed that, using prod.2, X
generates Λ. X generates any number of
b’s. Thus X generates the strings generated
by b*
. It may also be observed that the
above CFG generates the language
expressed by (b*
ab*
ab*
)*
.
9/14/2022 18

19. Example
Consider the following CFG
 = {a,b}
productions:
S → aSa|bSb|a|b|Λ
The above CFG generates the language
PALINDROME. It may be noted that the
CFG
S → aSa|bSb|a|b generates the language
NON-NULLPALINDROME.
9/14/2022 19

20. Example
Consider the following CFG
 = {a,b}
productions:
S → aSb|ab|Λ
It can be observed that the CFG generates the
language {an
bn
: n=0,1,2,3, …}. It may also be
noted that the language {an
bn
: n=1,2,3, …} can
be generated by the following CFG S → aSb|ab
9/14/2022 20

21. Ambiguous CFG
The CFG is said to be ambiguous if there exists atleast
one word of it’s language that can be generated by the
different production trees.
Example: Consider the following CFG S → aS|Sa|a
The word aaa can be generated by the following three
different trees
9/14/2022 21

22. Example continued …
Thus the above CFG is ambiguous, while the CFG
S → aS|a is not ambiguous as neither the word
aaa nor any other word can be derived from
more than one production trees. The derivation
tree for aaa is as follows
S
a S
a S
a
S
a S
S a
a
S
S a
S a
a
9/14/2022 22

23. Trees
As in English language any sentence can be
expressed by parse tree, so any word generated
by the given CFG can also be expressed by the
parse tree, e.g.
consider the following CFG
S → AA
A → AAA|bA|Ab|a
Obviously, baab can be generated by the above
CFG. To express the word baab as a parse tree,
start with S. Replace S by the string AA, of
nonterminals, drawing the downward lines
from S to each character of this string as follows
9/14/2022 23

24. Trees continued …
Now let the left A be replaced by bA and the right one
by Ab then the tree will be
S
A A
S
A A
b A A b
9/14/2022 24

25. Trees continued …
Replacing both A’s by a, the above tree will be
S
A A
b A A b
a a
9/14/2022 25

26. Trees continued …
Thus the word baab is generated. The above tree to
generate the word baab is called Syntax tree or
Generation tree or Derivation tree as well.
9/14/2022 26

27. Chomsky Normal Form
Chomsky Normal Form (CNF): If a CFG has
only productions of the form
nonterminal → string of two nonterminals
or
nonterminal → one terminal
then the CFG is said to be in Chomsky Normal
Form (CNF).
9/14/2022 27

28. Note
It is to be noted that any CFG can be converted to be in
CNF, if the null productions and unit productions are
removed. Also if a CFG contains nullable productions
as well, then the corresponding new production are
also to be added. Which leads the following theorem
9/14/2022 28

29. Theorem
All NONNULL words of the CFL can be
generated by the corresponding CFG
which is in CNF i.e. the grammar in CNF
will generate the same language except
the null string.
Following is an example showing that a
CFG in CNF generates all nonnull words
of corresponding CFL.
9/14/2022 29

30. Example
Consider the following CFG
S → aSa|bSb|a|b|aa|bb
To convert the above CFG to be in CNF,
introduce the new productions as
A → a, B → b, then the new CFG will be
S → ASA|BSB|AA|BB|a|b
A → a
B → b
9/14/2022 30

31. Example continued …
Introduce nonterminals R1 and R2 so that
S → AR1|BR2|AA|BB|a|b
R1 → SA
R2 → SB
A → a
B → b
which is in CNF.
It may be observed that the above CFG which is in
CNF generates the NONNULLPALINDROME,
which does not contain the null string.
9/14/2022 31

32. Example
Consider the following CFG
S → ABAB
A → a|Λ
B → b|Λ
Here S → ABAB is nullable production and A
→ Λ, B → Λ are null productions. Removing
the null productions
A → Λ and B → Λ, and introducing the new
productions as
S → BAB|AAB|ABB|ABA|AA|AB|BA|BB|A|B
9/14/2022 32

33. Example continued …
Now S → A|B are unit productions to be
eliminated as shown below
S → A gives S → a (using A → a)
S → B gives S → b (using B → b)
Thus the new resultant CFG takes the form
S → BAB|AAB|ABB|ABA|AA|AB|BA|BB|a|b A
→ a
B → b
Introduce the nonterminal C where C → AB, so
that
9/14/2022 33

34. Example continued …
S →
BAB|AAB|ABB|ABA|AA|AB|BA|BB|a|b
A → a
B → b
C → AB
S → CC|BC|AC|CB|CA|AA|C|BA|BB|a|b
is the CFG in CNF.
9/14/2022 34

35. Example
To construct an FA that accepts the grammar
S→ abA
A→ baB
B→ aA|bb
The language can be identified by the three
words generated as follows
(i) S → abA
→ abbaB (using A→ baB)
→ abba bb (using B→ bb)
9/14/2022 35

36. (ii) S → abA
→ abbaB (using A→ baB)
→ abbaaA (using B→ aA)
→ abbaabaB (using A→ baB)
→ abbaababb (using B→ bb)
(iii) S → abA
→ abbaB (using A→ baB)
→ abbaaA (using B→ aA)
→ abbaabaB (using A→ baB)
→ abbaabaaA (using B→ aA)
→ abbaabaabaB (using A→ baB)
→ abbaabaababb (using B→ bb)
9/14/2022 36

37. Example continued …
which shows that corresponding language has RE
abba(aba)*
bb. Thus the FA accepting the given CFG
may be
b
b
a
b
b a
a,b
a b
a
b
a
a
A B +
S-
a,b
9/14/2022 37

38. Left most derivation
Definition: The derivation of a word w,
generated by a CFG, such that at each step, a
production is applied to the left most
nonterminal in the working string, is said to be
left most derivation.
It is to be noted that the nonterminal that
occurs first from the left in the working string,
is said to be left most nonterminal. Following
is an example
9/14/2022 38

39. Example
Consider the following CFG
S→ XY
X → XX|a
Y→ YY|b
then following are the two left most
derivations of aaabb
9/14/2022 39

40. Example continued …
S → XY
→ XXY
→ aXY
→ aXXY
→ aaXY
→ aaaY
→ aaaYY
→ aaabY
= aaabb
S → XY
→ XXY
→ XXXY
→ aXXY
→ aaXY
→ aaaY
→ aaaYY
→ aaabY
= aaabb
9/14/2022 40

41. Thanks...
9/14/2022 41