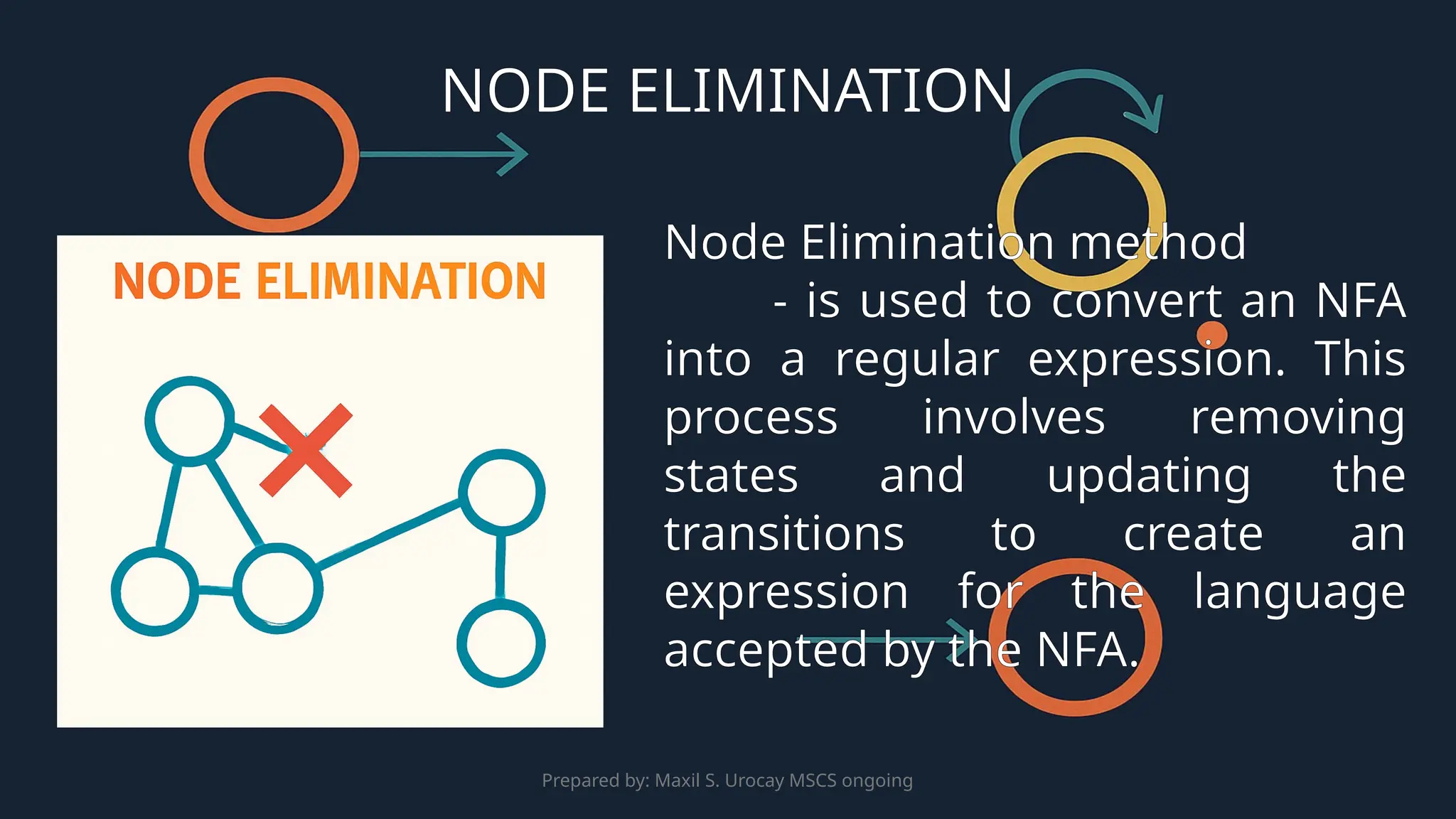
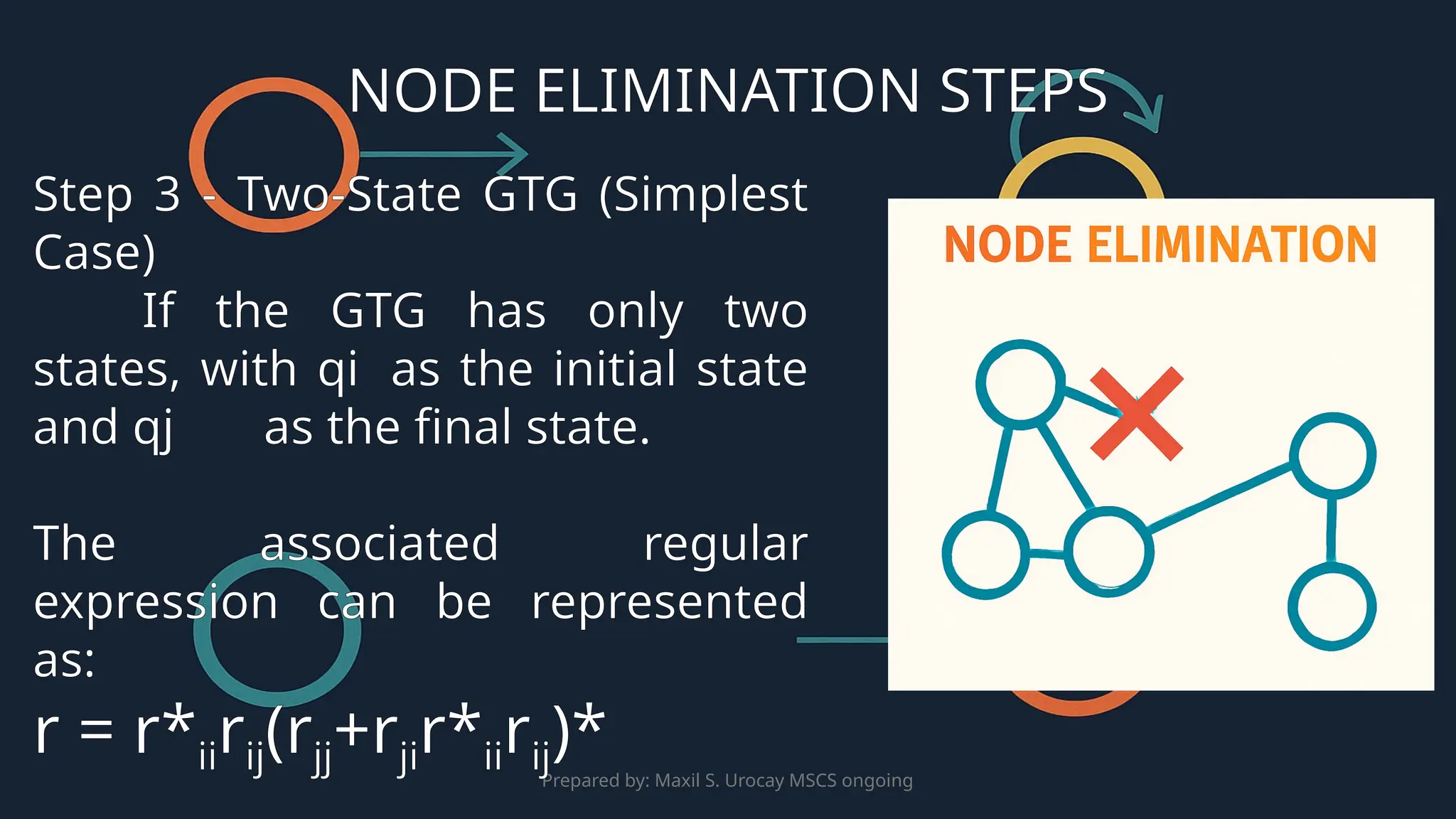
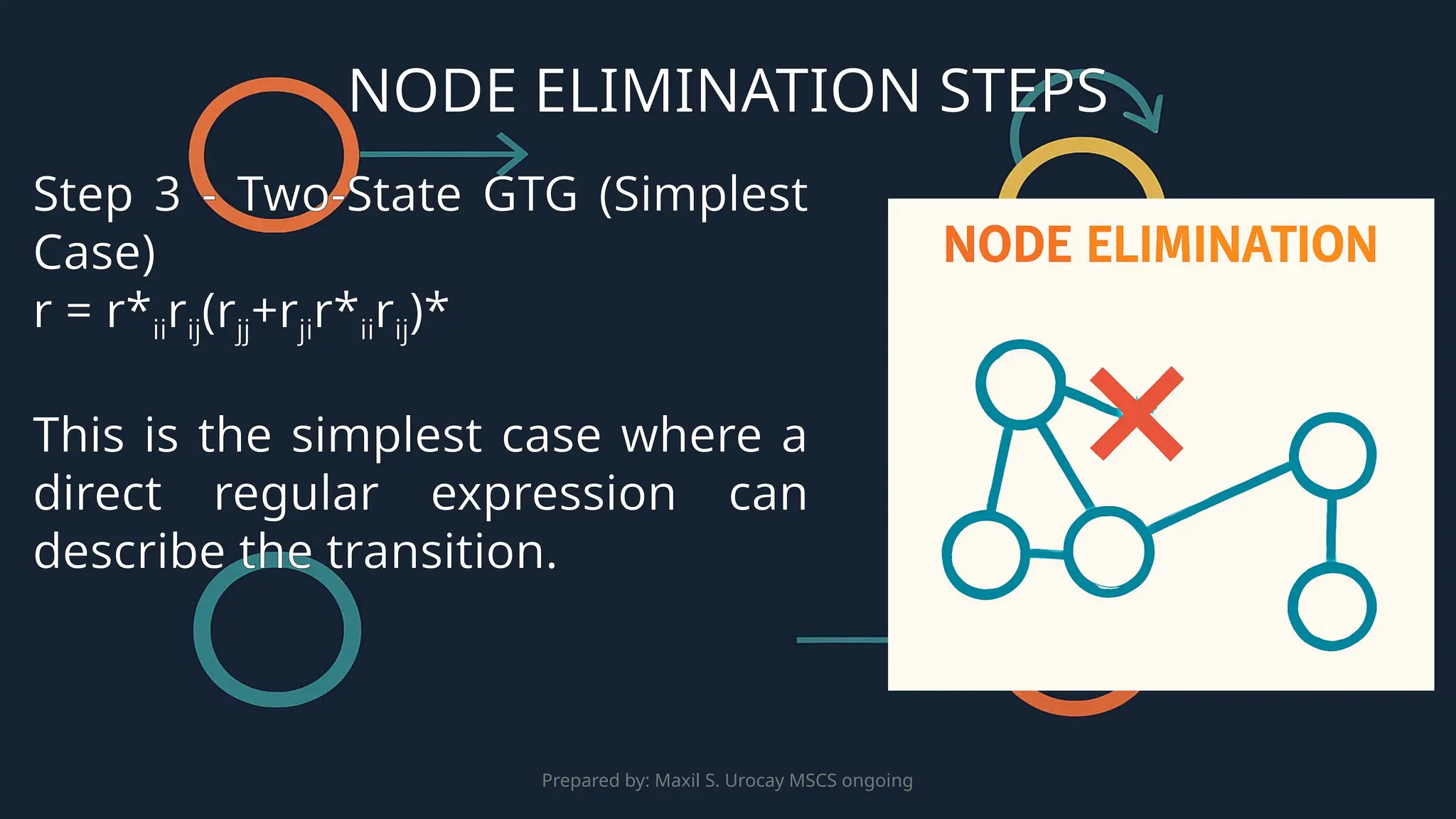
This presentation explores the process of converting a Non-Deterministic Finite Automaton (NFA) to a Regular Expression (RE). It introduces the Node Elimination method, which involves removing states from the NFA and replacing transitions with regular expressions to represent the accepted language. The process is outlined through a Generalized Transition Graph (GTG), which provides a flexible way to handle various transitions, including λ-transitions. The presentation covers key steps in this conversion process, including handling two-state and three-state GTGs, and provides examples and simplifications to help create the final regular expression for the NFA's language.

1. AUTOMATA AND
COMPILER THEORIES
AND FORMAL
LANGUAGES
Prepared by: Maxil S. Urocay MSCS ongoing

2. Prepared by: Maxil S. Urocay MSCS ongoing
“Prayer to the Holy Spirit by St. Augustine”
Breathe in me, O Holy Spirit,
That my thoughts may all be holy.
Act in me, O Holy Spirit,
That my work, too may be holy.
Draw my heart, O Holy Spirit.
That I love but what is holy.
Strengthen me, O Holy Spirit,
To defend all that is holy.

3. NFA TO RE
(NON-DETERMINISTIC
FINITE AUTOMATA TO
REGULAR EXPRESSION
CONVERSION)
Prepared by: Maxil S. Urocay MSCS ongoing

4. Prepared by: Maxil S. Urocay MSCS ongoing
Node Elimination method
- is used to convert an NFA
into a regular expression. This
process involves removing
states and updating the
transitions to create an
expression for the language
accepted by the NFA.
NODE ELIMINATION

5. Prepared by: Maxil S. Urocay MSCS ongoing
The goal is to transform an
NFA into a regular expression
that describes the language
accepted by the NFA.
The Node Elimination
method, which involves
progressively eliminating states
and creating regular
expressions that describe
transitions.
NFA TO RE PROCESS

6. Prepared by: Maxil S. Urocay MSCS ongoing
A Generalized Transition
Graph (GTG) is a modified
version of a regular transition
graph where:
The edges between states are
labeled with regular expressions
rather than just symbols.
GENERALIZED TRANSITION GRAPH
(GTG)

7. Prepared by: Maxil S. Urocay MSCS ongoing
A Generalized Transition Graph
(GTG) is a modified version of a
regular transition graph where:
It allows more flexibility, enabling us
to represent multiple transitions,
including λ-transitions (empty string
transitions) and transitions involving
more than one symbol.
GENERALIZED TRANSITION GRAPH
(GTG)

8. Prepared by: Maxil S. Urocay MSCS ongoing
GTGs are essential because
they provide a complete way to
represent the transitions of an
NFA, which can then be used to
create regular expressions.
ROLE IN NFA TO RE CONVERSION

9. Prepared by: Maxil S. Urocay MSCS ongoing
The GTG helps in
systematically removing states
while ensuring that the regular
expression still accurately
describes the language accepted
by the NFA.
ROLE IN NFA TO RE CONVERSION

10. Prepared by: Maxil S. Urocay MSCS ongoing
Each edge in the GTG is
labeled with a regular
expression that describes the
transition between two states.
A GTG can handle multiple
transitions and represents the
relationship between states
more flexibly.
GENERALIZED TRANSITION GRAPH
(GTG)

11. Prepared by: Maxil S. Urocay MSCS ongoing
It allows us to transform the
NFA into a complete graph where
each edge is labeled with a
regular expression.
WHY DO WE USE GTGs IN NFA TO
RE CONVERSION

12. Prepared by: Maxil S. Urocay MSCS ongoing
Once the NFA is converted
into a GTG, we can
systematically apply the Node
Elimination method to eliminate
states and form the final regular
expression.
WHY DO WE USE GTGs IN NFA TO
RE CONVERSION

13. Prepared by: Maxil S. Urocay MSCS ongoing
- Convert the NFA to a GTG.
- Remove states and replace
transitions with regular
expressions.
- Simplify the resulting regular
expression.
- Continue until the correct regular
expression is obtained.
NFA TO RE PROCESS OVERVIEW

14. Prepared by: Maxil S. Urocay MSCS ongoing
Step 1 - Start with an NFA
Begin with an NFA with
states q0,q1,...,qn​ and a single
final state distinct from the initial
state.
Ensure that the NFA has clear
initial and final states, and the
initial and final states are distinct.
NODE ELIMINATION STEPS

15. Prepared by: Maxil S. Urocay MSCS ongoing
Step 2 - Convert the NFA into a
Complete Generalized Transition
Graph (GTG)
Let rij​ represents the regular
expression on the edge from qi​to
qj​
.
NODE ELIMINATION STEPS

16. Prepared by: Maxil S. Urocay MSCS ongoing
Step 2 - Convert the NFA into a
Complete Generalized Transition
Graph (GTG)
If the NFA has q0​to q1​transition
labeled as "a", then in the GTG,
this edge is labeled r01​
=a.
NODE ELIMINATION STEPS

17. Prepared by: Maxil S. Urocay MSCS ongoing
Step 3 - Two-State GTG (Simplest
Case)
If the GTG has only two
states, with qi ​as the initial state
and qj ​as the final state.
The associated regular
expression can be represented
as:
r = r*iirij(rjj+rjir*iirij)*
NODE ELIMINATION STEPS

18. Prepared by: Maxil S. Urocay MSCS ongoing
Step 3 - Two-State GTG (Simplest
Case)
r = r*iirij(rjj+rjir*iirij)*
This is the simplest case where a
direct regular expression can
describe the transition.
NODE ELIMINATION STEPS

19. Prepared by: Maxil S. Urocay MSCS ongoing
Step 4 - Three-State GTG
If the GTG has three states,
with: qp as the initial state, qf ​
as
the final state, and qk as an
intermediate state.
Introduce new edges with the
regular expression:
r=rpq+rpkr*kkrkq
NODE ELIMINATION STEPS

20. Prepared by: Maxil S. Urocay MSCS ongoing
Step 4 - Three-State GTG
r=rpq+rpkr*kkrkq
We remove the intermediate
state qk by creating a regular
expression that combines the
transitions between qp ​ and qf​
,
going through qk ​
.
NODE ELIMINATION STEPS

21. Prepared by: Maxil S. Urocay MSCS ongoing
Step 5 - GTG with Four or More
States
If the GTG has four or more
states, pick a state qk to be
removed.
Apply Step 4 for all pairs of states
(qi ​
,qj​
), where i≠k and j≠k.
NODE ELIMINATION STEPS

22. Prepared by: Maxil S. Urocay MSCS ongoing
Step 5 - GTG with Four or More
States
Simplifying rules:
r+ =r
∅
r =
⋅∅ ∅
∅*=ϵ
When done, remove state qk​and
update the graph with the new
regular expressions.
NODE ELIMINATION STEPS

23. Prepared by: Maxil S. Urocay MSCS ongoing
Step 5 - GTG with Four or More
States
As we remove each state, the
transitions that pass through that
state are replaced by new regular
expressions. Simplify the
expressions wherever possible.
NODE ELIMINATION STEPS

24. Prepared by: Maxil S. Urocay MSCS ongoing
Step 6 - Repeat Until the Final
Regular Expression is Obtained
Repeat Steps 3 to 5 until the
correct regular expression for the
NFA is obtained.
The process will continue until all
unnecessary states are removed,
leaving a final regular expression.
NODE ELIMINATION STEPS

25. Prepared by: Maxil S. Urocay MSCS ongoing
The final regular expression
represents the NFA's language.
After following the above steps,
the regular expression might look
like:
r=a*b(c+da*b)*
FINAL REGULAR EXPRESSION

26. Prepared by: Maxil S. Urocay MSCS ongoing
r=a*b(c+da*b)*
This regular expression can now
be used to describe the strings
accepted by the original NFA.
FINAL REGULAR EXPRESSION

27. Prepared by: Maxil S. Urocay MSCS ongoing
L = {w ε {0, 1}* | the number of
0’s is even and the number of 1’s
is odd}
NFA TO RE EXAMPLE

28. SHORT QUIZ
Prepared by: Maxil S. Urocay MSCS ongoing

29. Prepared by: Maxil S. Urocay MSCS ongoing
Instructions:
- Draw the transition graph of the NFA.
- Apply the state elimination method to
convert the NFA to a regular expression.
- Show all steps clearly, including the
state removal and the updated regular
expressions for each transition.
- Identify the language of the given
automaton graph.
NFA TO RE EXAMPLE