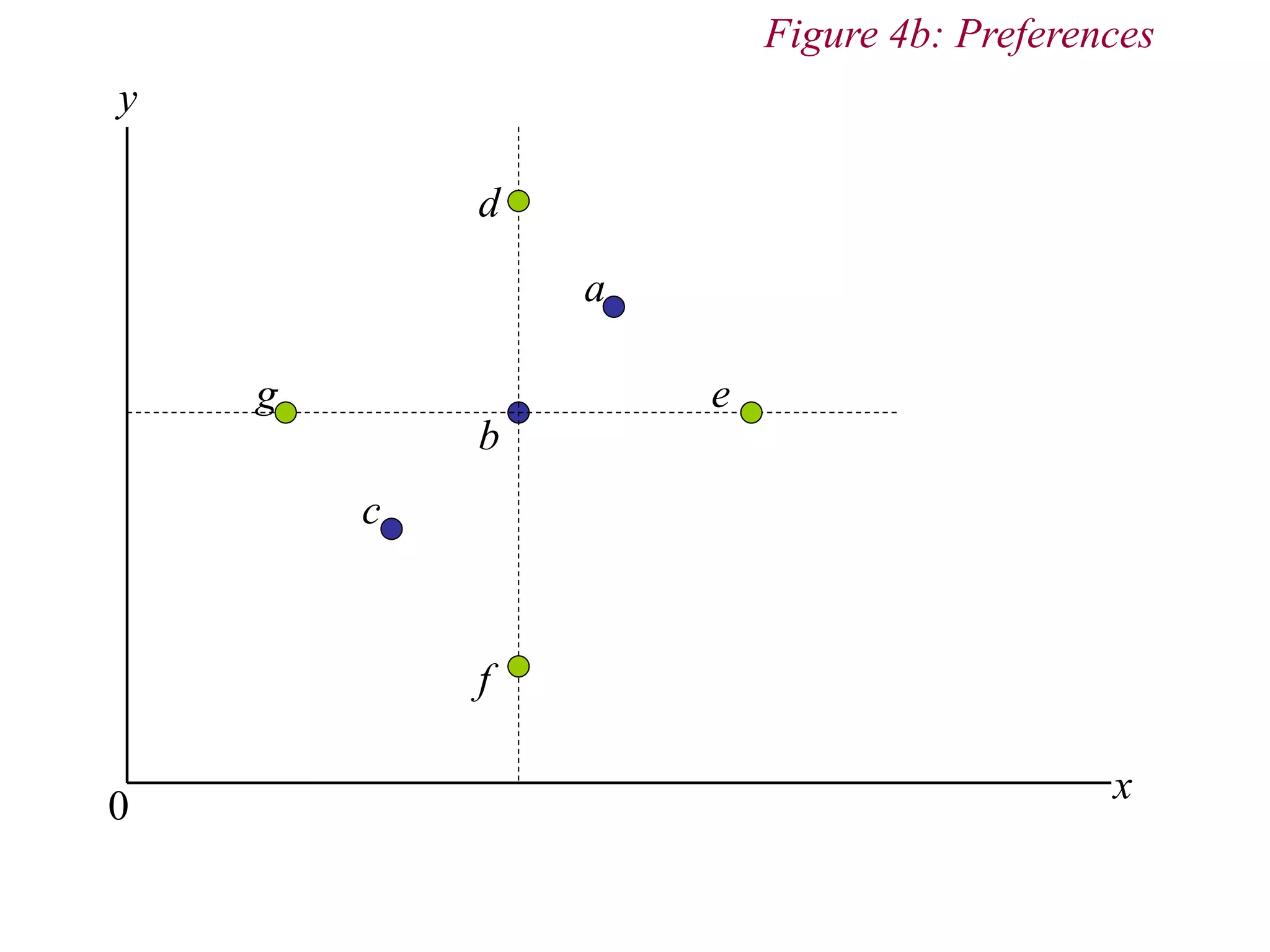
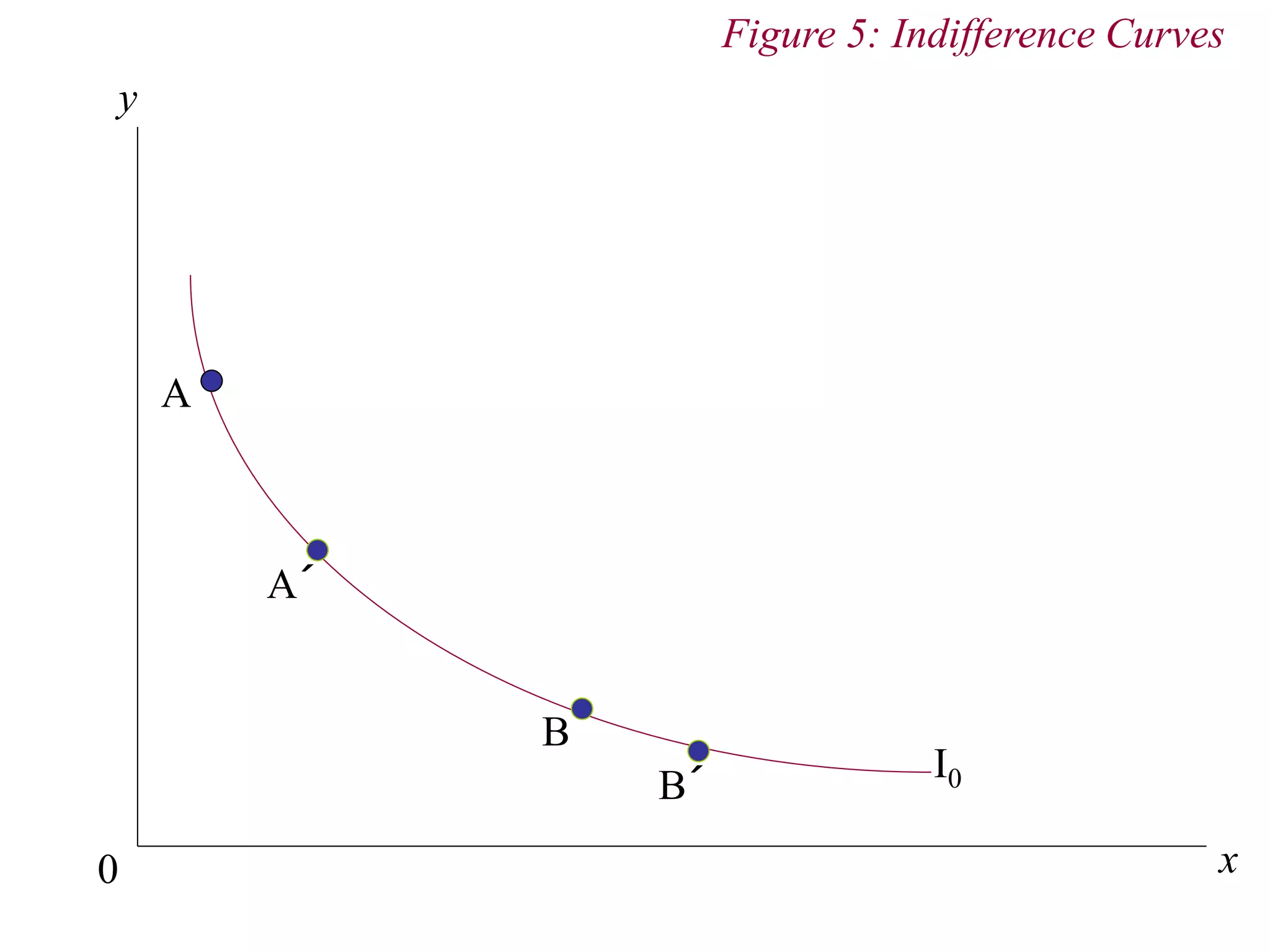
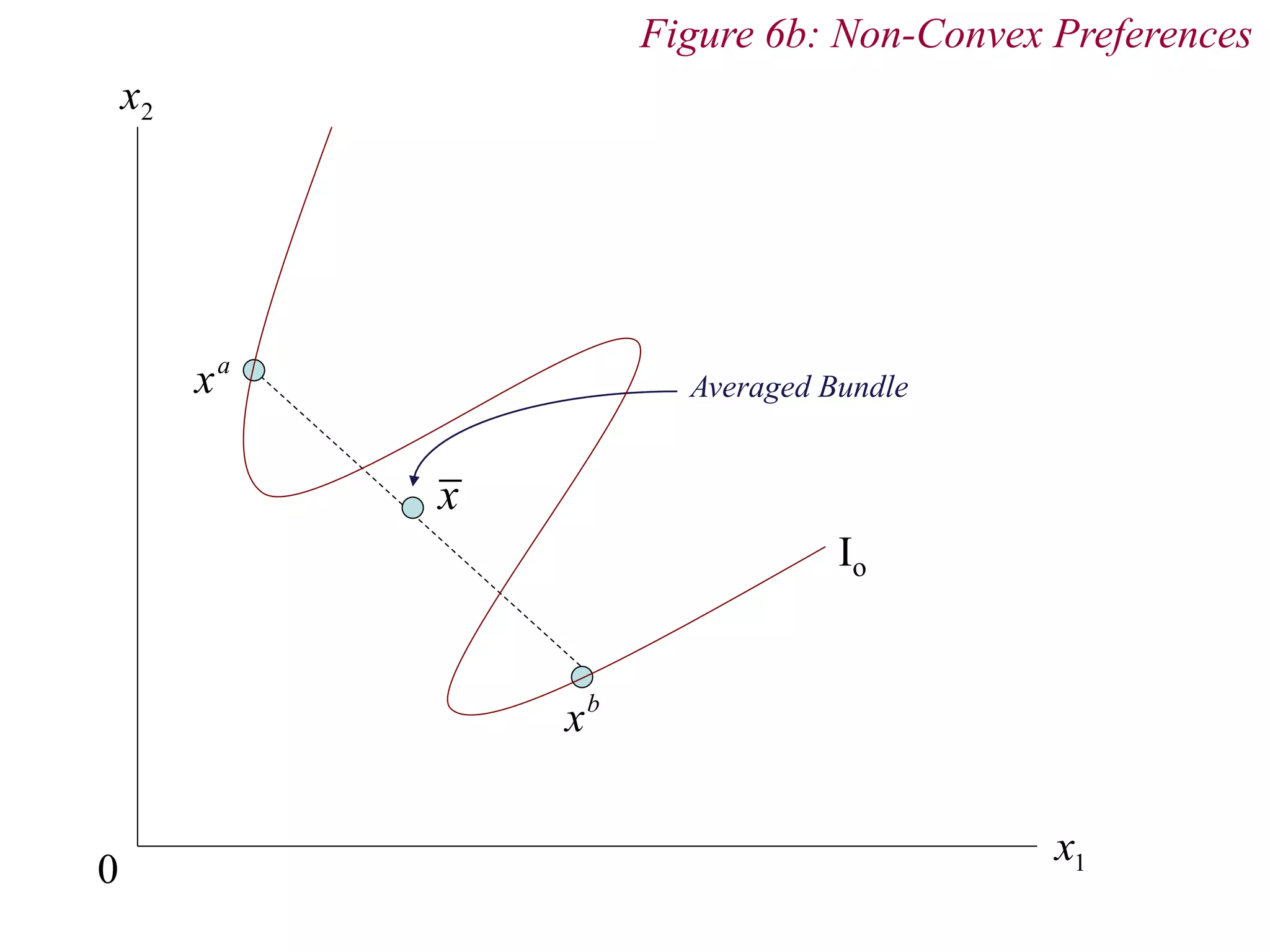
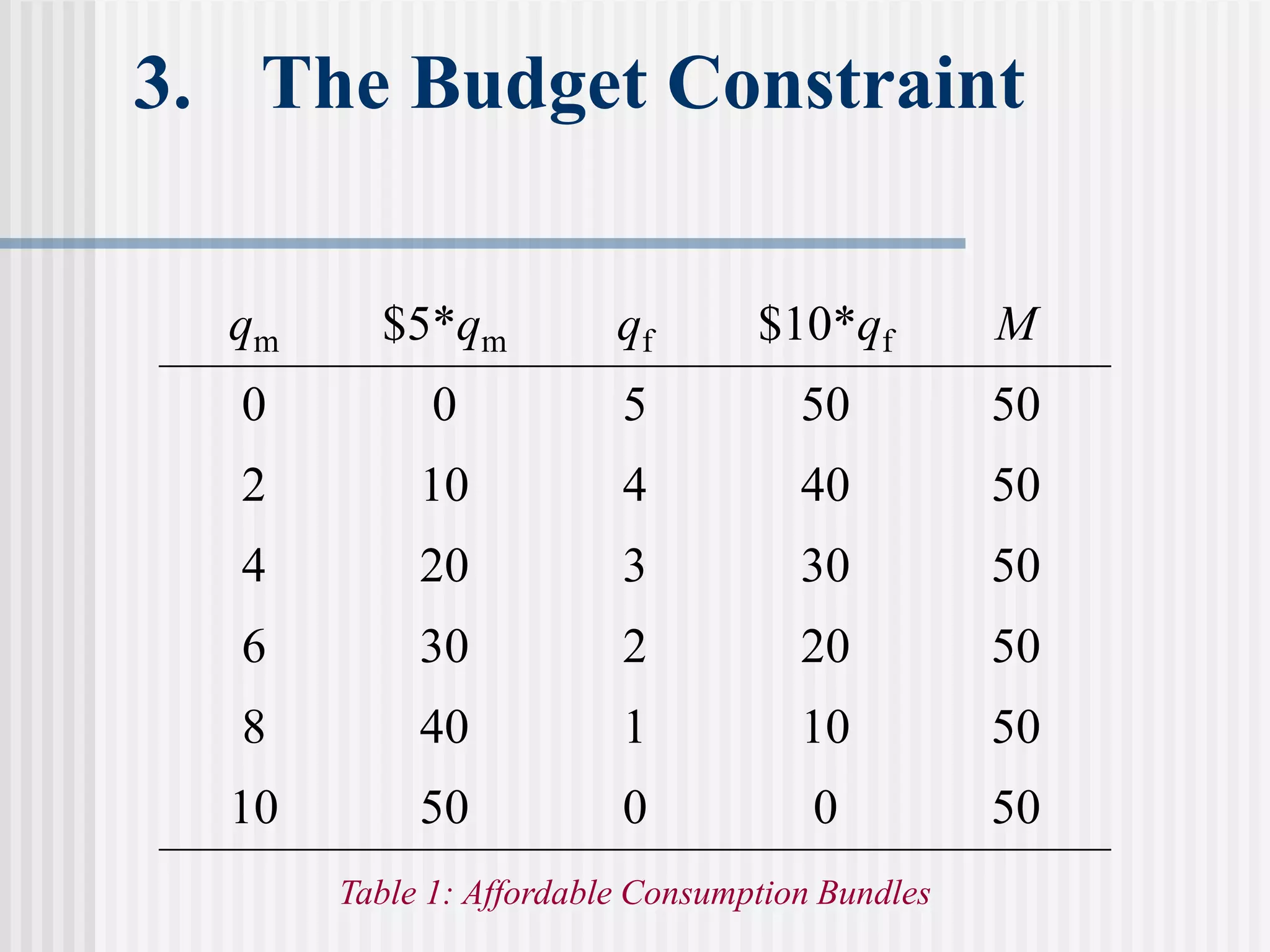
The document provides an overview of consumer theory and the budget constraint in microeconomics. It discusses how consumers maximize utility given their preferences for goods and a budget constraint determined by income and prices. Specifically, it defines the budget constraint graphically using indifference curves, explains how the slope of the budget line represents the trade-off between goods, and discusses how taxes, subsidies and rationing can impact the budget constraint. It also outlines the key assumptions of consumer preferences including completeness, consistency, non-satiation, and diminishing marginal rate of substitution.

1. Economics 3030
Intermediate Microeconomic Theory
Topic 2: Consumer Theory (ii)

2. 1. Introduction
 We have seen how demand curves may be used to
represent consumer behaviour.
 But we said very little about the nature of the
demand curve; why it slopes down for example.
 Now we go ‘behind’ the demand curve
 i.e. we investigate how buyers reconcile what they
want with what they can get

3. 1. Introduction
 N.B. We can use this theory in many ways - not
simply as household consumer buying goods.
 For example:
 Modelling decision of worker as regards his supply
of labour (i.e. demand for leisure)
 Allocation of income across time (saving and
investment)

4. 2. Theory of Consumer Choice
 Four elements:
(i) Consumer’s income
(ii) Prices of goods
(iii) Consumer’s tastes
(iv) Rational Maximisation

5. 3. The Budget Constraint
 The first two elements define the budget constraint
 The feasibility of the consumer’s desired
consumption bundle depends upon two factors:
(i) Income
(ii) Prices
 Note: We assume, for the time being, that both are
exogenous (i.e. beyond consumer's control)

6. 3. The Budget Constraint
 Example (N.B two goods)
 Two goods - films and meals
 Student grant = $50 per week (p.w.)
 Price of meal = $5
 Price of film = $10

7. 3. The Budget Constraint
 Thus student can ‘consume’ maximum p.w. of 10
meals or 5 films by devoting all of his grant to the
consumption of only one of these goods.
 Alternatively, he can consume some combination of
the two goods
 For example, giving up one film a week (saving $10)
enables student to buy two additional meals (costing
$5 each)
.

8. 3. The Budget Constraint
qm $5*qm qf $10*qf M
0 0 5 50 50
2 10 4 40 50
4 20 3 30 50
6 30 2 20 50
8 40 1 10 50
10 50 0 0 50
Table 1: Affordable Consumption Bundles

9. Films
0
Meals
A
B
Figure 1: Budget Constraint
2 8 10
1
4
5

10. Films
0
Meals
Figure 1: Budget Constraint
Budget Line
Budget (Feasible) Set

11. 3. The Budget Constraint
 The budget constraint defines the maximum
affordable quantity of one good available to the
consumer given the quantity of the other good that
is being consumed.
 N.B. Trade-off!
 Trade-off is represented slope of budget
constraint.

12. 3. The Budget Constraint
 Intercepts
Determined by income divided by the appropriate
price of the good
Define maximum quantity of a particular good
available to an individual
 Slope
Independent of income
Determined only by relative prices
• .

13. 3. The Budget Constraint
 If consumer is devoting all income to films (qf =
$50/$10 = 5), then 1 meal can only be obtained by
sacrificing consumption of some films.
 How many films must consumer give up?
 pm = $5; thus to obtain that $5, the consumer must
give up 1/2 a film

14. 3. The Budget Constraint
 The slope of the budget constraint in this
example is thus:
-
pm
pf
= -
$5
$10
= -
1
2

15. Films
0
Meals
Figure 2: Slope of Budget Constraint
1 10
4.5
5
Dqm
=1
Dqf
= -0.5

16. 3. The Budget Constraint
 More generally:
 Two goods (x,y), prices (px, py) and money income
(m)
 m = pxx + pyy
 Slope of budget constraint: - px/py

17. 3. The Budget Constraint
 Proof:
m = px
x + py
y
Þ
py
y = m - px
x
Þ
y =
m
py
-
px
py
x

18. 3. The Budget Constraint
 Thus:
 Such that
y =
m
py
æ
è
ç
ö
ø
÷
a
-
px
py
æ
è
ç
ö
ø
÷
b
x
Þ
y = a - bx
Dy = -bDx = -
px
py
æ
è
ç
ö
ø
÷ Dx

19. y
0
x
A
B
Figure 3: Budget Constraint
y = m/py - (px/py)x
m/px
m/py
Dx
Dy = -
px
py
æ
è
ç
ö
ø
÷ Dx

20. 3. The Budget Constraint
 Intuition:
 If additional units of x costs px
 Then their purchase requires a change in
consumption of y of –(px/py) (i.e. a sacrifice of y)
in order to maintain the budget constraint.

21. 3. The Budget Constraint
 Economic Rate of Substitution (ERS)
Amount of y the consumer is obliged to
sacrifice for one extra unit of x
 ERS = –(px/py)
 Slope of budget line

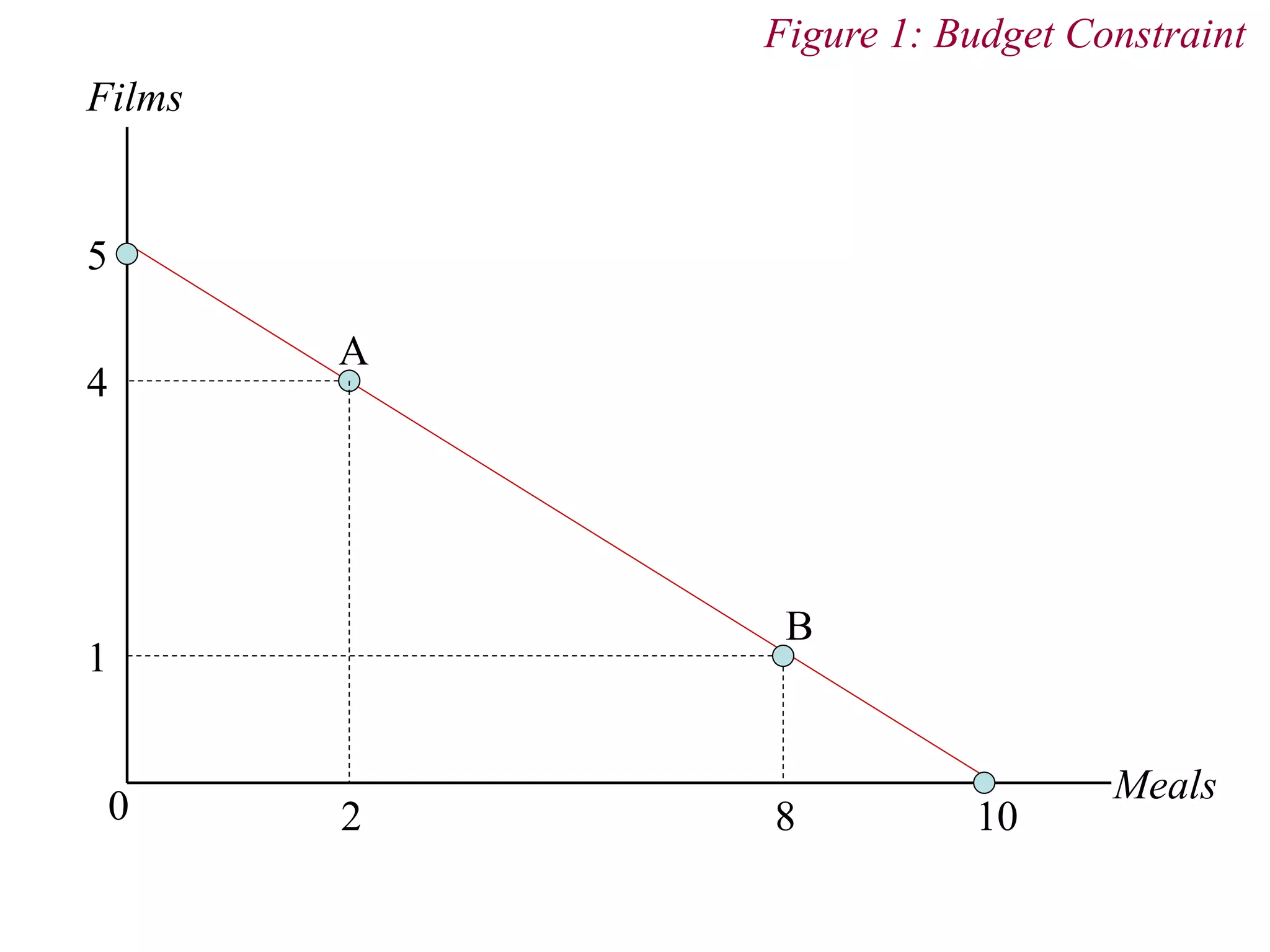
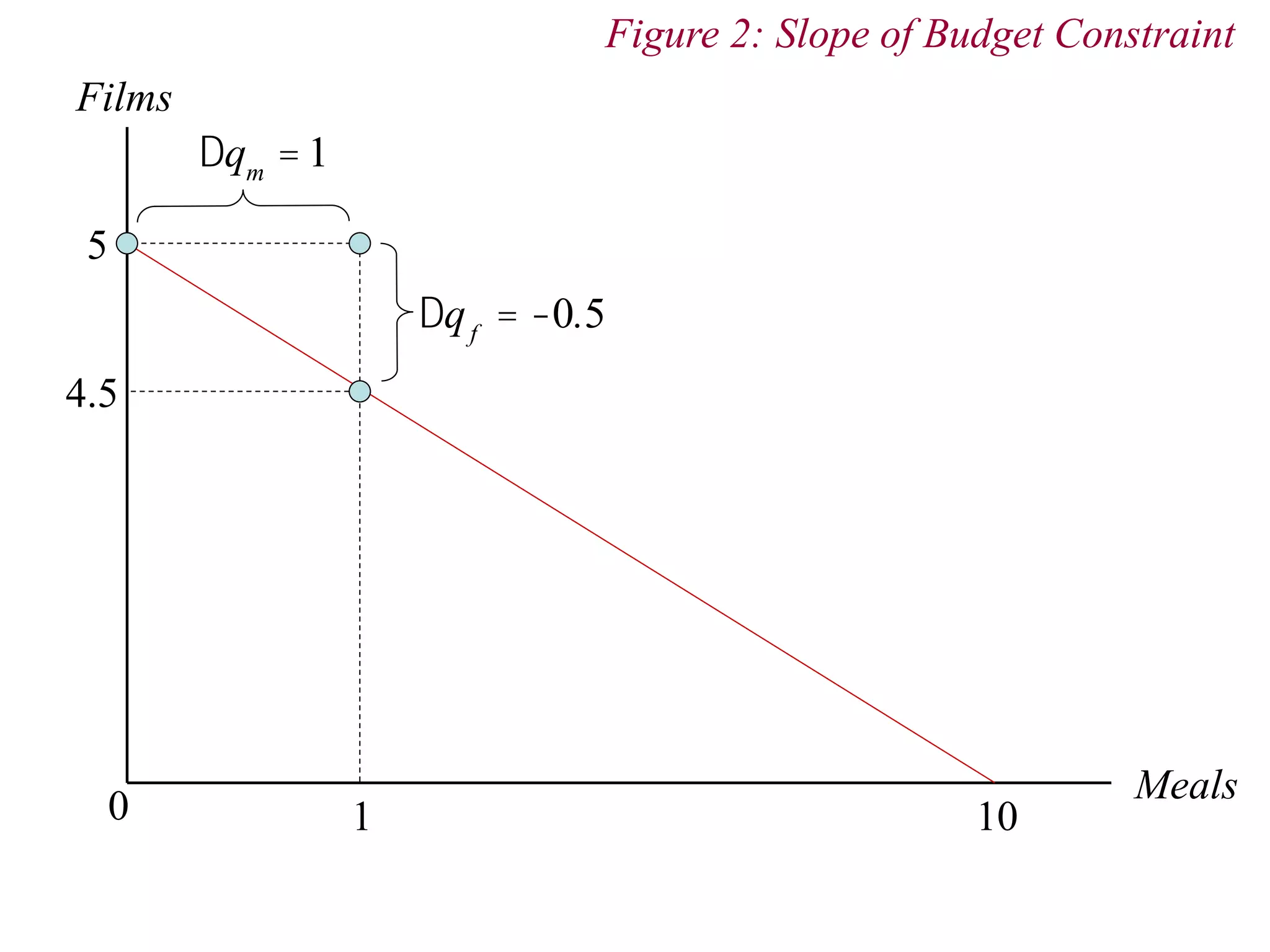
22. 3. Budget Constraint
 Taxes and Subsidies
Taxes can be imposed per unit (i.e. p + t) or ad
valorem [i.e. p(1+ t)]
 Subsidies are ‘negative’ taxes
 Rationing causes budget constraint to become
vertical or horizontal

23. y
0 m/px
Figure 4: Budget Constraint and Rationing
m/py
x
x

24. y
0 xt m/px
Figure 5: Budget Constraint and Taxation
m/py
x
Slope = -(px/py)
Slope = -[(px+t)/py]
x

25. 4. Preferences
 Consider now the consumer’s preferences; given
what consumer can do, what would he like to do?
 Four assumptions:
(i) Completeness
(ii) Consistency
(iii) Non-satiation
(iv) Diminishing Marginal Rate of Substitution

26. 4. Preferences
 Completeness
Consumers can rank alternative bundles according
to the satisfaction or utility they provide
Thus, given two bundles a and b, then ,
or
Preferences assumed only to be ordinal, not
cardinal; i.e. consumer simply has to be able to say
he prefers a to b, not to say by how much.
a ≻ b a ≻ b
a ≻ b

27. 4. Preferences
 Consistency
Preferences are also assumed to be consistent
Thus if and , then we would infer that
We assume consumer is logically consistent
a ≻ b a ≻ c
a ≻ c

28. 4. Preferences
 Non-satiation
Consumers assumed to always prefer more
‘goods’ to less.
We can accommodate economics ‘bads’ (e.g.
pollution) in this assumption by interpreting then
as ‘negative’ goods
 We can illustrate the first three assumptions
graphically as follows

29. y
0
x
a
Figure 4a: Preferences
c
b

30. y
0
x
a
Figure 4b: Preferences
c
f
d
e
g
b

31. y
0
x
a
Figure 4c: Preferences
b
c
f
d
e
g
h
i

32. y
0
x
a
Figure 4d: Preferences
b
c
f
d
e
g
h
i
Indifference Curve

33. 4. Preferences
 Marginal Rate of Substitution (MRS)
The quantity of y (i.e. the ‘vertical’ good) the consumer
must sacrifice to increase the quantity of x (i.e. ‘the
horizontal’ good) by one unit without changing total utility.
 We generally assume (smooth) diminishing MRS
 To hold utility constant, diminishing quantities of
one good must be sacrificed to obtain successive
equal increases in the quantity of the other good.

34. 4. Preferences
 Diminishing MRS derives from underlying
assumption of diminishing marginal utility
 Marginal utility of a good is defined as the change
in a consumer’s total utility from consuming the
good divided by the change in his consumption of
the good
 Diminishing MRS assumes that the increase in
utility from consuming additional units of a good
is declining

35. 4. Preferences
 Non-satiation implies downward sloping
indifference curves; increases in one good require
sacrifices in the other good to hold total utility
constant.
 However, we can go further; diminishing MRS
implies that indifference curves are convex to
origin, becoming flatter as we move to the right.
 Indeed, the MRS of x for y is simply the slope of
the indifference curve

36. y
x
0
I0
Figure 5: Indifference Curves

37. y
x
0
Figure 5: Indifference Curves
A
B
I0

38. y
x
0
I0
Figure 5: Indifference Curves
A
B
A´
B´

39. y
x
0
I0
Figure 5: Indifference Curves
A
B
A´
B´
Dy
Dy
Dx =1
Dx =1

40. 4. Preferences
 Diminishing MRS implies consumers prefer
consumption bundles containing mixtures of
goods rather than extremes
 For example, Bundle C = (5, 5) preferred to both
Bundle A = (2, 8) and Bundle B = (8, 2)
 Diminishing MRS (i.e. diminishing marginal
utility)

41. y
x
0
I0
Figure 6: Indifference Curves
A
B

42. y
x
0
I0
Figure 6: Indifference Curves
A
B
8
2
2 8

43. y
x
0
I0
Figure 6: Indifference Curves
A
B
8
2
2 5 8
5
C
I1

44. 4. Preferences
 Formally, such preferences are said to be convex
 Note also:
 Non-convex preferences
 Concave preferences

45. 0
xa
xb
x2
x1
Io
Averaged Bundle
x
Figure 6a: Convex Preferences

46. 0
xa
xb
x2
x1
Io
Averaged Bundle
x
Figure 6b: Non-Convex Preferences

47. 0
xa
xb
x2
x1
Io
Averaged Bundle
x
Figure 6c: Concave Preferences

48. 4. Preferences
 Note:
(i) Any point on the indifference map must lay on
an indifference curve;
and
(ii) indifference curves cannot cross
 Thus every point on the indifference map must lay
on one and only one indifference curve

49. y
x
0
I0
I1
I2
Figure 7: Indifference Curves

50. y
x
0
I1
I0
Figure 8: Indifference Curves Cannot Cross
a
b
c

51. 4. Preferences
 Non-Standard Preferences
 Perfect Substitutes
 Perfect Complements
 Neutral Goods
 Satiation and Bliss Points

52. 0
x2
x1
I0
I1
I2
Figure 8a: Perfect Substitutes

53. 0
x2
x1
I0
I1
I2
b = x2 x1
Figure 8b: Perfect Complements

54. 4. Preferences
 Comparing preferences
 Slope of indifference curve (MRS) measures
relative intensity of consumer’s demand
 Steeper (flatter) indifference curves implies
relatively higher (lower) demand for horizontal
good (x)