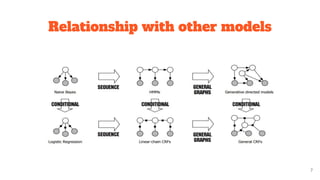
Conditional Random Fields (CRFs) are a probabilistic framework used for structured prediction, particularly in applications such as natural language processing and image recognition. They model the conditional distribution of output labels given input data, leveraging contextual information from previous labels. CRFs allow for highly expressive feature functions without needing to model distribution over irrelevant variables, thus enhancing prediction accuracy.

1. Conditional Random Fields
a popular probabilistic method for structured prediction
Nishant Mahat 074MSCSK006
Rachana Kunwar 074MSCSK009
Suresh Mainali 074MSCSK014
Suresh Pokharel 074MSCSK015
Presented by:
M.Sc. in Computer System and Knowledge Engineering
Institute of Engineering, Pulchowk Campus

2. Background
● Markov Property
○ Process has Markov property when the value of the next state only
depends on the current state
○ Does not depend on the sequence of events that preceded it, but only on
the state that the model is in at that point
● Generative and Discriminative Models
○ A generative model is a joint distribution that models p(t, w) = p(t)p(w|t)
or p(w)p(t|w).
○ Generative describe how the output is probabilistically generated as a
function of the input
○ Discriminative focus solely on the conditional distribution p(y|x).
2

3. Background Cont...
● Discriminative model just cares about the conditional distribution p(t|w),
does not model p(w)
● In practice, estimating p(w)p(t|w) and then finding p(t|w) yields a different
answer than just finding p(t|w) directly. This is due to the fact that we never
actually have the true distribution in our training data.
3

4. Background Cont...
● Hidden Markov Model
○ Models a sequence of observations X = {xt} T t=1 by assuming that there is an underlying
sequence of states Y = {yt} T t=1 drawn from a finite state set S
○ To model the joint distribution p(y, x) tractably, an HMM makes two independence
assumptions.
○ It assumes that each state depends only on its immediate predecessor, that is, each state yt is
independent of all its ancestors y1, y2, . . . , yt−2 given the preceding state yt−1
It also assumes that each observation variable xt depends only on the current state yt
○ With these assumptions, we can specify an HMM using three probability distributions: first,
the distribution p(y1) over initial states; second, the transition distribution p(yt |yt−1); and
finally, the observation distribution p(xt |yt).
4

5. Introduction
● More commonly used variance of Markov Networks
● Undirected graphical model that is discriminative, used for predicting
sequences.
● Construct conditional model p(Y|X)
● Commonly used in pattern recognition, machine learning and used for
structured prediction.
● It uses contextual information from previous labels, thus increasing the
amount of information the model has to make a good prediction.
5

6. CRF - Definition
● Let G = (V, E) be a finite graph, and let A be a finite alphabet
● Y is indexed by the vertices of G
● Then (X,Y) is a conditional random field if the random variables Yv,
conditioned on X, obey the Markov property with respect to the graph:
● p(Y|X,Yw,w≠v) = p(Yv|X,Yw,w~v),
● where w~v means that w and v are neighbors in G
● Maximum random field were each random variable yi
is conditioned on the
complete input sequence x1
, …xn
6

7. Relationship with other models
7

8. Feature Function
● Expresses some characteristics of sequence that the data points represent
● Input :
● Set of input Vectors
● Position i of data point
● Label of data point i-1 in X
● Label of data point i in X
● Output : Any real value (Mostly 0 or 1)
● Feature function = f ( X , i , li-1
, li
)
8

9. Example: Part of Speech Tagging
In a CRF, each feature function is a function that takes in as input:
● a sentence s
● the position i of a word in the sentence
● the label lili of the current word
● the label li−1li−1 of the previous word
Output:
● f (X, i, L{i - 1}, L{i} ) = 1 if L{i - 1} is a Noun, and L{i} is a Verb. 0 otherwise
● f (X, i, L{i - 1}, L{i} ) = 1 if L{i - 1} is a Verb and L{i} is an Adverb. 0 otherwise.
9

10. Example: Part of Speech Tagging
10
Normalizing between 0 and 1 by exponentiating and normalizing:

11. Example Contd...
● Each feature function is based on label of previous word and current word
● Next, assign weights λj
to each feature function fj
.
● Use optimization algorithms, e.g. gradient descent, to learn the weights.
11

12. Applications of CRFs
● Natural Language Processing,
○ Parts-of-Speech tagging
○ Named Entity recognition
○ Parsing text
○ Extracting Proper nouns from sentences
● Parts-recognition in Images
● Estimating the score in a game
● Gene prediction
Conditional Random Fields can be used to predict any sequence in which multiple
variables depend on each other
12

13. Examples of use in vision
● Grid-shaped CRFs for pixel labelling (e.g. segmentation), using boosted
classifiers.
13

14. Conclusion
● Conditional Random Fields are a probabilistic framework for labeling and
segmenting structured data, such as sequences, trees.
● Don’t need to model distribution over variables, we don’t care about.
● Allows models with highly expressive features, without worrying about wrong
independencies.
● The primary advantage of CRFs is the relaxation of the independence
assumption
14

15. References
● https://medium.com/ml2vec/overview-of-conditional-random-fields-68a2a20fa
541
● https://arxiv.org/pdf/1011.4088.pdf
● https://www3.nd.edu/~dchiang/teaching/nlp/2015/notes/chapter8v1.pdf
15

16. Thank You!
16