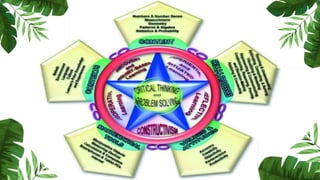
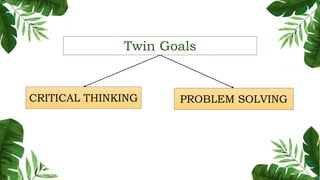
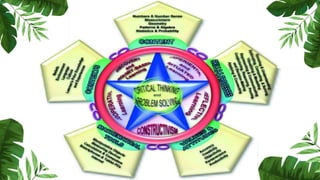
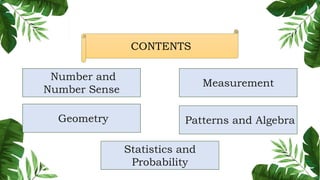
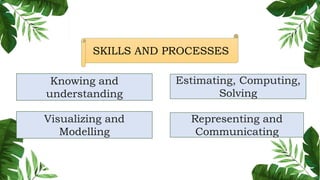
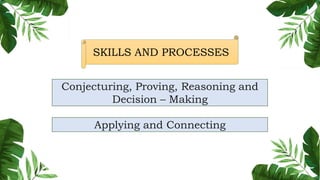
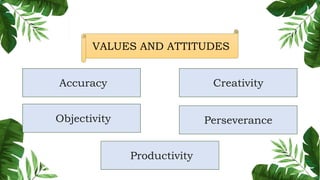
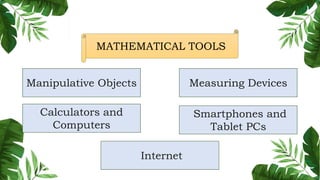
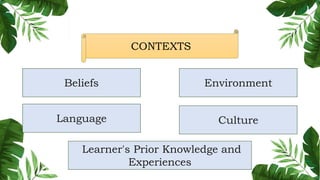
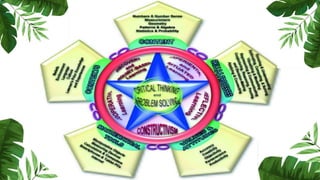
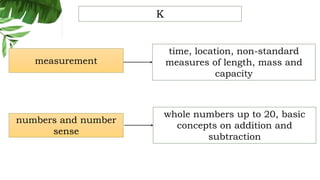
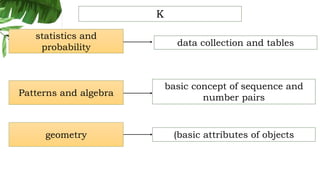
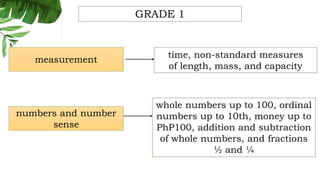
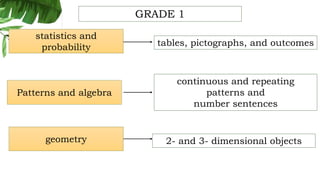
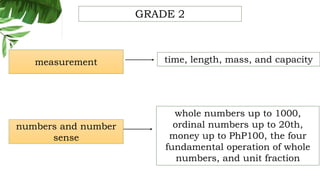
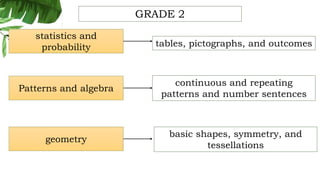
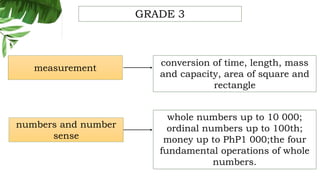
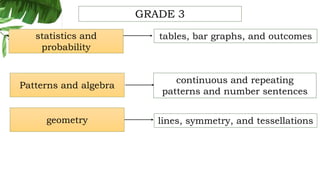
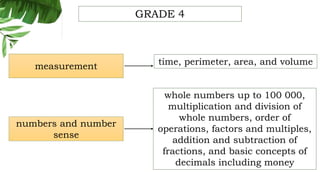
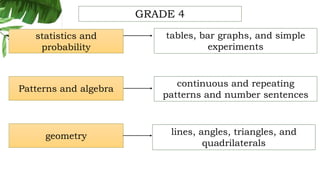
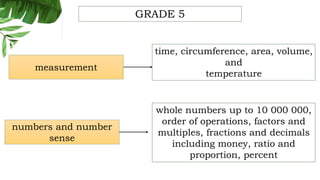
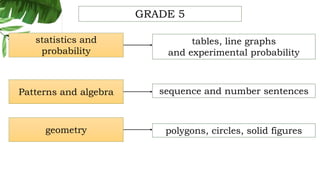
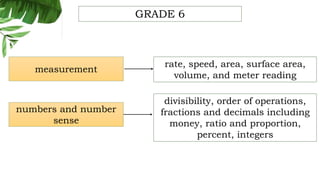
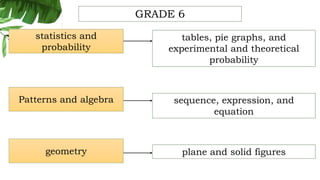
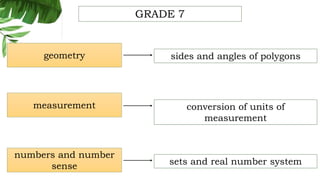
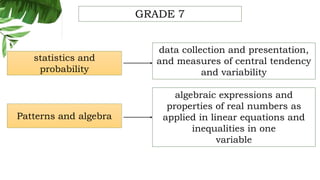
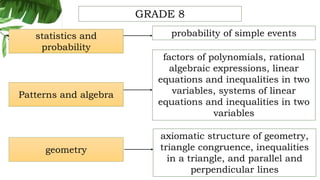
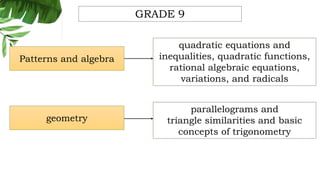
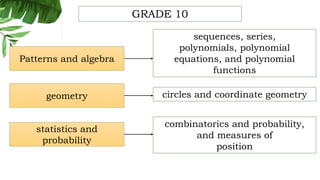
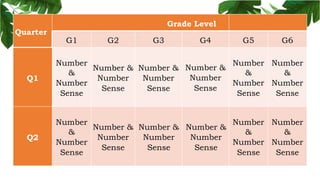
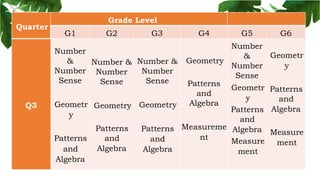
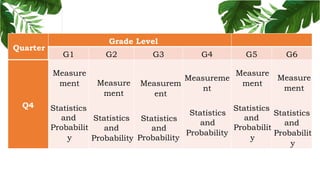
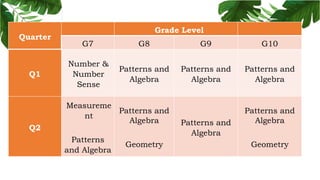
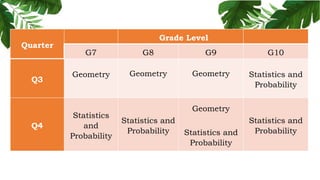
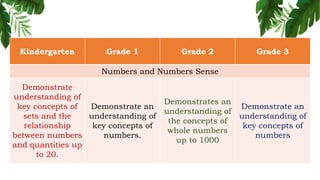
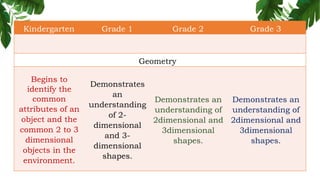
The document outlines the conceptual framework and pedagogical approaches of the Philippines K-12 mathematics curriculum. It describes the twin goals of critical thinking and problem solving. It also explains the spiral approach where mathematical concepts increase in depth and breadth as students progress through grades, ensuring a seamless transition in learning.