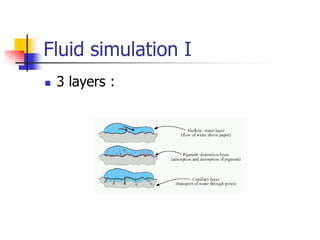
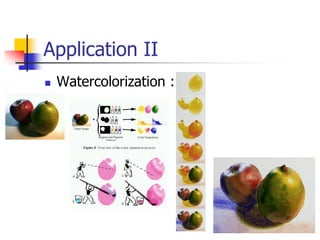
This document summarizes a 1997 paper on computer-generated watercolor painting. It describes how the paper simulates watercolor effects like flow, granulation and edge darkening through fluid simulation and applies the Kubelka-Munk model for optical rendering. Applications include interactive painting, watercolorizing photos, and applying effects to 3D models. While making assumptions, the model effectively captures watercolor's appearance for artistic purposes. Future work could explore additional effects and animation capabilities.

1. Computer Generated Watercolor
Curtis, Anderson, Seims, Fleisher, Salesin
SIGGRAPH 1997
Presented by
Yann SEMET
Universite of Illinois at Urbana Champaign
Universite de Technologie de Compiegne

2. Background
 NPR
 Purpose : aesthetic rather than
technical
 Artificial art ?

3. Harold Cohen – 80’s

4. Haeberli - 1990

5. Meier - 1995

6. Litwinowicz - 1997

7. Hertzmann – 1998, 2001

8. Gooch - 2001

9. Today : Curtis et al. - 1997

10. Overview
 Particularities of Watercolor
 Computer simulation
 Fluid simulation
 Kubelka-Munk rendering
 Applications
 Discussion

11. Like no other medium
 Beautiful textures and patterns
 Reveals the motion of water
 Luminous, glowing

12. Blake (1757-1827)

13. Turner (1775-1851)

14. Constable (1776-1837)

15. Cezanne (1839-1906)

16. Kandinski (1866-1944)

17. Klee (1879-1940)

18. Carter (1955-)

19. Watercolor materials
 Paper
 Pigments

20. Watercolor effects
a) Dry brush d) Granulation
b) Edge darkening e) Flow
c) Back runs f) Glazing

21. Simulation..

22. Fluid simulation I
 3 layers :

23. Fluid simulation II
 Parameters of the simulation :
 Wet-area mask : M
 Velocities : u,v
 Pressure : p
 Concentration : gk
 Height of paper : h
 Physical properties : density, staining power,
granularity, etc.
 Fluid properties : saturation, capacity, etc.

24. Paper simulation
 Supposedly : shape of every fiber
matters
 A simpler model : a height field
 Generation : Perlin’s noise and Worley’s
cellular textures

25. Main loop
 For each time step
 Move Water
 Update velocities
 Relax Divergence
 Flow Outward
 Move Pigment
 Transfer Pigment
 Simulate Capillary Flow

26. Conditions for realism
 Flow must be constrained so water
remains within M
 Surplus of water causes flow outward
 Flow must be damped to minimize
oscillating waves
 Flow is perturbed by texture of paper
 Local changes have global effects
 Outward flow to darken edges

27. Rendering : Kubelka-Munk
 For each pigment, 2 coeff. Per RGB layer :
 K : absorbtion
 S : scattering
 Supposedly : K and S are measured
 Here : user provides Rw and Rb

28. Types of paints
 Opaque (e.g. Indian Red)
 Transparent (e.g. Quinacridone Rose)
 Interference (e.g. Interference Lilac)
 Different hues (e.g. Hansa Yellow)

29. Optical compositing
 Compute R and T :
 Then compose :
 Weight relatively to relative thicknesses

30. Discussion of the KM model
 Assumptions partially satisfied :
 Identical refractive indices
 Random orientation of pigments
 Diffuse illumination
 1 wavelength at a time
 No chemical interaction
 Works surprisingly well !
 OK, because we’re looking for appearance,
not actual modeling

31. Application I
 Interactive painting :

32. Application II
 Watercolorization :

33. Application III
 3D models :

34. Future work
 Other effects
 Automatic rendering
 Generalization
 Animation

35. Summary
 A particular painting technique
 A physically based simulation
 Fluid motion
 Optical compositing
 Application and results

36. Conclusion and discussion
 Efficiency issues and long term interest
 Border between art, physics and
computer science