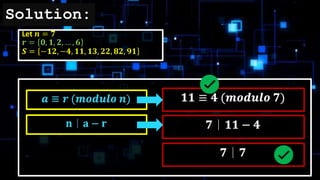
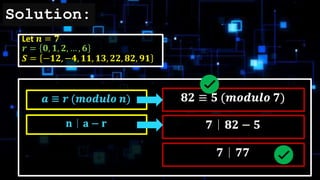
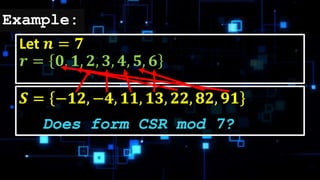
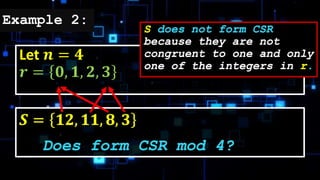
The document defines a complete system of residues as a set of n integers modulo n that each correspond to the residues 0, 1, ..., n-1. It provides examples of complete systems of residues for n=7 and n=4, with sets of integers that each cover the possible residues when divided by n. The complete system of residues contains one and only one integer corresponding to each possible residue.