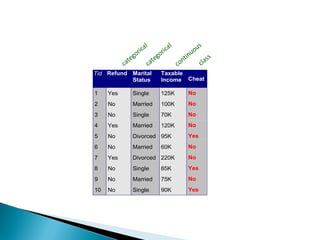
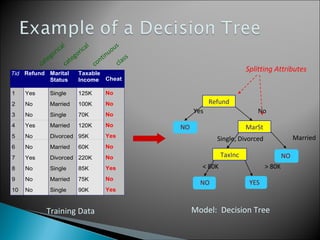
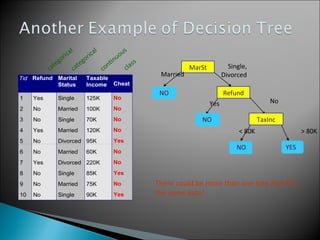
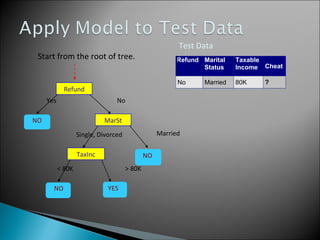
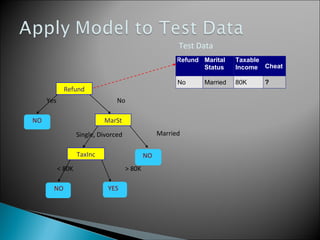
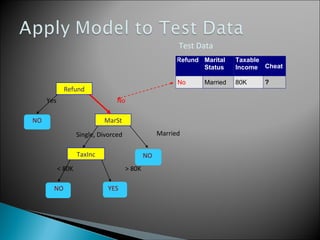
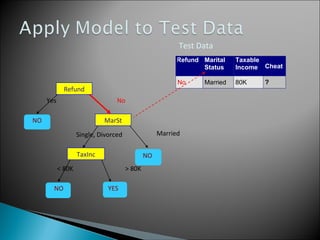
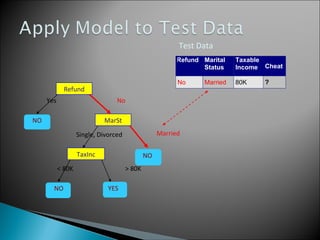
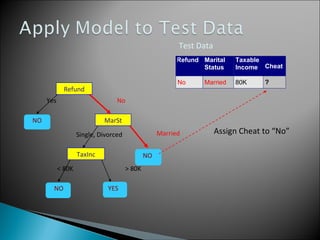
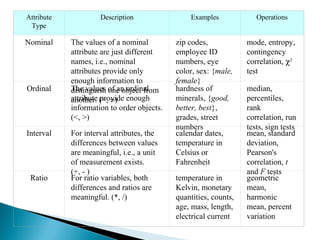
The document discusses classification, which involves using a training dataset containing records with attributes and classes to build a model that can predict the class of previously unseen records. It describes dividing the dataset into training and test sets, with the training set used to build the model and test set to validate it. Decision trees are presented as a classification method that splits records recursively into partitions based on attribute values to optimize a metric like GINI impurity, allowing predictions to be made by following the tree branches. The key steps of building a decision tree classifier are outlined.

1. Classification

2.  Given a collection of records (training set )
◦ Each record contains a set of attributes, one of the
attributes is the class.
 Find a model for class attribute as a function of
the values of other attributes.
 Goal: previously unseen records should be
assigned a class as accurately as possible.
◦ A test set is used to determine the accuracy of the
model. Usually, the given data set is divided into
training and test sets, with training set used to build
the model and test set used to validate it.

3. Tid Refund Marital
Status
Taxable
Income Cheat
1 Yes Single 125K No
2 No Married 100K No
3 No Single 70K No
4 Yes Married 120K No
5 No Divorced 95K Yes
6 No Married 60K No
7 Yes Divorced 220K No
8 No Single 85K Yes
9 No Married 75K No
10 No Single 90K Yes
10
categorical
categorical
continuous
class
Refund Marital
Status
Taxable
Income Cheat
No Single 75K ?
Yes Married 50K ?
No Married 150K ?
Yes Divorced 90K ?
No Single 40K ?
No Married 80K ?
10
Test
Set
Training
Set
Model
Learn
Classifier

4.  Direct Marketing
◦ Goal: Reduce cost of mailing by targeting a set of
consumers likely to buy a new cell-phone product.
◦ Approach:
 Use the data for a similar product introduced before.
 We know which customers decided to buy and which decided
otherwise. This {buy, don’t buy} decision forms the class
attribute.
 Collect various demographic, lifestyle, and company-interaction
related information about all such customers.
 Type of business, where they stay, how much they earn, etc.
 Use this information as input attributes to learn a classifier
model.
From [Berry & Linoff] Data Mining Techniques, 1997

5.  Fraud Detection
◦ Goal: Predict fraudulent cases in credit card
transactions.
◦ Approach:
 Use credit card transactions and the information on its account-
holder as attributes.
 When does a customer buy, what does he buy, how often he pays
on time, etc
 Label past transactions as fraud or fair transactions. This forms
the class attribute.
 Learn a model for the class of the transactions.
 Use this model to detect fraud by observing credit card
transactions on an account.

6.  Customer Attrition:
◦ Goal: To predict whether a customer is likely to be lost to
a competitor.
◦ Approach:
 Use detailed record of transactions with each of the past and
present customers, to find attributes.
 How often the customer calls, where he calls, what time-of-the
day he calls most, his financial status, marital status, etc.
 Label the customers as loyal or disloyal.
 Find a model for loyalty.
From [Berry & Linoff] Data Mining Techniques, 1997

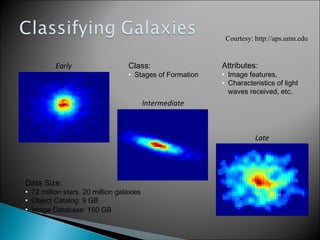
7.  Sky Survey Cataloging
◦ Goal: To predict class (star or galaxy) of sky objects,
especially visually faint ones, based on the telescopic
survey images (from Palomar Observatory).
 3000 images with 23,040 x 23,040 pixels per image.
◦ Approach:
 Segment the image.
 Measure image attributes (features) - 40 of them per object.
 Model the class based on these features.
 Success Story: Could find 16 new high red-shift quasars, some
of the farthest objects that are difficult to find!
From [Fayyad, et.al.] Advances in Knowledge Discovery and Data Mining, 1996

8. Early
Intermediate
Late
Data Size:
• 72 million stars, 20 million galaxies
• Object Catalog: 9 GB
• Image Database: 150 GB
Class:
• Stages of Formation
Attributes:
• Image features,
• Characteristics of light
waves received, etc.
Courtesy: http://aps.umn.edu

9.  Decision Tree based Methods
 Rule-based Methods
 Memory based reasoning
 Neural Networks
 Naïve Bayes and Bayesian Belief Networks
 Support Vector Machines

10. Decision
Tree

18. Tid Refund Marital
Status
Taxable
Income Cheat
1 Yes Single 125K No
2 No Married 100K No
3 No Single 70K No
4 Yes Married 120K No
5 No Divorced 95K Yes
6 No Married 60K No
7 Yes Divorced 220K No
8 No Single 85K Yes
9 No Married 75K No
10 No Single 90K Yes
10
categorical
categorical
continuous
class

19. Tid Refund Marital
Status
Taxable
Income Cheat
1 Yes Single 125K No
2 No Married 100K No
3 No Single 70K No
4 Yes Married 120K No
5 No Divorced 95K Yes
6 No Married 60K No
7 Yes Divorced 220K No
8 No Single 85K Yes
9 No Married 75K No
10 No Single 90K Yes
10
categorical
categorical
continuous
class
Refund
MarSt
TaxInc
YESNO
NO
NO
Yes No
MarriedSingle, Divorced
< 80K > 80K
Splitting Attributes
Training Data Model: Decision Tree

20. Tid Refund Marital
Status
Taxable
Income Cheat
1 Yes Single 125K No
2 No Married 100K No
3 No Single 70K No
4 Yes Married 120K No
5 No Divorced 95K Yes
6 No Married 60K No
7 Yes Divorced 220K No
8 No Single 85K Yes
9 No Married 75K No
10 No Single 90K Yes
10
categorical
categorical
continuous
class
MarSt
Refund
TaxInc
YESNO
NO
NO
Yes No
Married
Single,
Divorced
< 80K > 80K
There could be more than one tree that fits
the same data!

21. Refund
MarSt
TaxInc
YESNO
NO
NO
Yes No
MarriedSingle, Divorced
< 80K > 80K
Refund Marital
Status
Taxable
Income Cheat
No Married 80K ?
10
Test Data
Start from the root of tree.

22. Refund
MarSt
TaxInc
YESNO
NO
NO
Yes No
MarriedSingle, Divorced
< 80K > 80K
Refund Marital
Status
Taxable
Income Cheat
No Married 80K ?
10
Test Data

23. Refund
MarSt
TaxInc
YESNO
NO
NO
Yes No
MarriedSingle, Divorced
< 80K > 80K
Refund Marital
Status
Taxable
Income Cheat
No Married 80K ?
10
Test Data

24. Refund
MarSt
TaxInc
YESNO
NO
NO
Yes No
MarriedSingle, Divorced
< 80K > 80K
Refund Marital
Status
Taxable
Income Cheat
No Married 80K ?
10
Test Data

25. Refund
MarSt
TaxInc
YESNO
NO
NO
Yes No
MarriedSingle, Divorced
< 80K > 80K
Refund Marital
Status
Taxable
Income Cheat
No Married 80K ?
10
Test Data

26. Refund
MarSt
TaxInc
YESNO
NO
NO
Yes No
MarriedSingle, Divorced
< 80K > 80K
Refund Marital
Status
Taxable
Income Cheat
No Married 80K ?
10
Test Data
Assign Cheat to “No”

27.  Collection of data objects and
their attributes
 An attribute is a property or
characteristic of an object
◦ Examples: eye color of a
person, temperature, etc.
◦ Attribute is also known as
variable, field, characteristic, or
feature
 A collection of attributes
describe an object
◦ Object is also known as record,
point, case, sample, entity, or
instance
Tid Refund Marital
Status
Taxable
Income Cheat
1 Yes Single 125K No
2 No Married 100K No
3 No Single 70K No
4 Yes Married 120K No
5 No Divorced 95K Yes
6 No Married 60K No
7 Yes Divorced 220K No
8 No Single 85K Yes
9 No Married 75K No
10 No Single 90K Yes
10
Attributes
Objects

28.  Attribute values are numbers or symbols assigned
to an attribute
 Distinction between attributes and attribute values
◦ Same attribute can be mapped to different attribute values
 Example: height can be measured in feet or meters
◦ Different attributes can be mapped to the same set of
values
 Example: Attribute values for ID and age are integers
 But properties of attribute values can be different
 ID has no limit but age has a maximum and minimum value

29.  There are different types of attributes
◦ Nominal
 Examples: ID numbers, eye color, zip codes
◦ Ordinal
 Examples: rankings (e.g., taste of potato chips on a scale
from 1-10), grades, height in {tall, medium, short}
◦ Interval
 Examples: calendar dates, temperatures in Celsius or
Fahrenheit.
◦ Ratio
 Examples: temperature in Kelvin, length, time, counts

30.  The type of an attribute depends on which of the
following properties it possesses:
◦ Distinctness: = ≠
◦ Order: < >
◦ Addition: + -
◦ Multiplication: * /
◦ Nominal attribute: distinctness
◦ Ordinal attribute: distinctness & order
◦ Interval attribute: distinctness, order & addition
◦ Ratio attribute: all 4 properties

31. Attribute
Type
Description Examples Operations
Nominal The values of a nominal
attribute are just different
names, i.e., nominal
attributes provide only
enough information to
distinguish one object from
another. (=, ≠)
zip codes,
employee ID
numbers, eye
color, sex: {male,
female}
mode, entropy,
contingency
correlation, χ2
test
Ordinal The values of an ordinal
attribute provide enough
information to order objects.
(<, >)
hardness of
minerals, {good,
better, best},
grades, street
numbers
median,
percentiles,
rank
correlation, run
tests, sign tests
Interval For interval attributes, the
differences between values
are meaningful, i.e., a unit
of measurement exists.
(+, - )
calendar dates,
temperature in
Celsius or
Fahrenheit
mean, standard
deviation,
Pearson's
correlation, t
and F tests
Ratio For ratio variables, both
differences and ratios are
meaningful. (*, /)
temperature in
Kelvin, monetary
quantities, counts,
age, mass, length,
electrical current
geometric
mean,
harmonic
mean, percent
variation

32. Attribute
Level
Transformation Comments
Nominal Any permutation of values If all employee ID numbers
were reassigned, would it
make any difference?
Ordinal An order preserving change of
values, i.e.,
new_value = f(old_value)
where f is a monotonic function.
An attribute encompassing
the notion of good, better
best can be represented
equally well by the values
{1, 2, 3} or by { 0.5, 1,
10}.
Interval new_value =a * old_value + b
where a and b are constants
Thus, the Fahrenheit and
Celsius temperature scales
differ in terms of where
their zero value is and the
size of a unit (degree).
Ratio new_value = a * old_value Length can be measured in
meters or feet.

33.  Discrete Attribute
◦ Has only a finite or countably infinite set of values
◦ Examples: zip codes, counts, or the set of words in a collection of
documents
◦ Often represented as integer variables.
◦ Note: binary attributes are a special case of discrete attributes
 Continuous Attribute
◦ Has real numbers as attribute values
◦ Examples: temperature, height, or weight.
◦ Practically, real values can only be measured and represented using
a finite number of digits.
◦ Continuous attributes are typically represented as floating-point
variables.

34.  Greedy strategy.
◦ Split the records based on an attribute test that optimizes
certain criterion.
 Issues
◦ Determine how to split the records
 How to specify the attribute test condition?
 How to determine the best split?
◦ Determine when to stop splitting

35.  Greedy strategy.
◦ Split the records based on an attribute test that optimizes
certain criterion.
 Issues
◦ Determine how to split the records
 How to specify the attribute test condition?
 How to determine the best split?
◦ Determine when to stop splitting

36.  Depends on attribute types
◦ Nominal
◦ Ordinal
◦ Continuous
 Depends on number of ways to split
◦ 2-way split
◦ Multi-way split

37.  Multi-way split: Use as many partitions as distinct
values.
 Binary split: Divides values into two subsets.
Need to find optimal partitioning.
CarType
Family
Sports
Luxury
CarType
{Family,
Luxury} {Sports}
CarType
{Sports,
Luxury} {Family} OR

38.  Multi-way split: Use as many partitions as distinct
values.
 Binary split: Divides values into two subsets.
Need to find optimal partitioning.
 What about this split?
Size
Small
Medium
Large
Size
{Medium,
Large} {Small}
Size
{Small,
Medium} {Large}
OR
Size
{Small,
Large} {Medium}

39.  Different ways of handling
◦ Discretization to form an ordinal categorical attribute
 Static – discretize once at the beginning
 Dynamic – ranges can be found by equal interval
bucketing, equal frequency bucketing
(percentiles), or clustering.
◦ Binary Decision: (A < v) or (A ≥ v)
 consider all possible splits and finds the best cut
 can be more compute intensive

41.  Used in CART, SLIQ, SPRINT.
 When a node p is split into k partitions (children), the
quality of split is computed as,
where, ni = number of records at child i,
n = number of records at node p.
∑=
=
k
i
i
split iGINI
n
n
GINI
1
)(

42. Splits into two partitions
Effect of Weighing partitions:
– Larger and Purer Partitions are sought for.
B?
Yes No
Node N1 Node N2
Parent
C1 6
C2 6
Gini = 0.500
N1 N2
C1 5 1
C2 2 4
Gini= 0.333
Gini(N1)
= 1 – (5/6)2
– (2/6)2
= 0.194
Gini(N2)
= 1 – (1/6)2
– (4/6)2
= 0.528
Gini(Children)
= 7/12 * 0.194 +
5/12 * 0.528
= 0.333

43.  For each distinct value, gather counts for each class in
the dataset
 Use the count matrix to make decisions
CarType
{Sports,
Luxury}
{Family}
C1 3 1
C2 2 4
Gini 0.400
CarType
{Sports}
{Family,
Luxury}
C1 2 2
C2 1 5
Gini 0.419
CarType
Family Sports Luxury
C1 1 2 1
C2 4 1 1
Gini 0.393
Multi-way split Two-way split
(find best partition of values)

44.  Use Binary Decisions based on one
value
 Several Choices for the splitting value
◦ Number of possible splitting values
= Number of distinct values
 Each splitting value has a count matrix
associated with it
◦ Class counts in each of the
partitions, A < v and A ≥ v
 Simple method to choose best v
◦ For each v, scan the database to
gather count matrix and compute its
Gini index
◦ Computationally Inefficient!
Repetition of work.

45.  For efficient computation: for each attribute,
◦ Sort the attribute on values
◦ Linearly scan these values, each time updating the count matrix and
computing gini index
◦ Choose the split position that has the least gini index
Cheat No No No Yes Yes Yes No No No No
Taxable Income
60 70 75 85 90 95 100 120 125 220
55 65 72 80 87 92 97 110 122 172 230
<= > <= > <= > <= > <= > <= > <= > <= > <= > <= > <= >
Yes 0 3 0 3 0 3 0 3 1 2 2 1 3 0 3 0 3 0 3 0 3 0
No 0 7 1 6 2 5 3 4 3 4 3 4 3 4 4 3 5 2 6 1 7 0
Gini 0.420 0.400 0.375 0.343 0.417 0.400 0.300 0.343 0.375 0.400 0.420
Split Positions
Sorted Values

46.  Entropy at a given node t:
(NOTE: p( j | t) is the relative frequency of class j at node t).
◦ Measures homogeneity of a node.
 Maximum (log nc) when records are equally distributed among
all classes implying least information
 Minimum (0.0) when all records belong to one class, implying
most information
◦ Entropy based computations are similar to the GINI index
computations
∑−= j
tjptjptEntropy )|(log)|()(

47.  Many Algorithms:
◦ Hunt’s Algorithm (one of the earliest)
◦ CART
◦ ID3, C4.5
◦ SLIQ,SPRINT

48. Thank You