수학

1. 프로그래머, 수학으로 생각하라
Chapter 1

2. Chapter 1
0 이야기

3. 이 장에서 배울 내용
10진법
2진법
숫자표기 기수법
0의 역할

4. 초등학교 1학년의 추억
선생님 : 공책을 펴고 ‘십이’라고 쓰세요.
필자 : 102
선생님 : 틀렸네요 12 라고 쓰는 겁니다.

5. 다양한 표기법….
‘십이’
아라비아 숫자 : 12
로마자 표기법 : ⅩⅡ
등등

6. 10 진법
• 사용하는 숫자 : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9  10종류
• 자릿수에 의미가 있으며 오른쪽 부터 1의자리, 10의자리, 100의 자리 자리로 표기

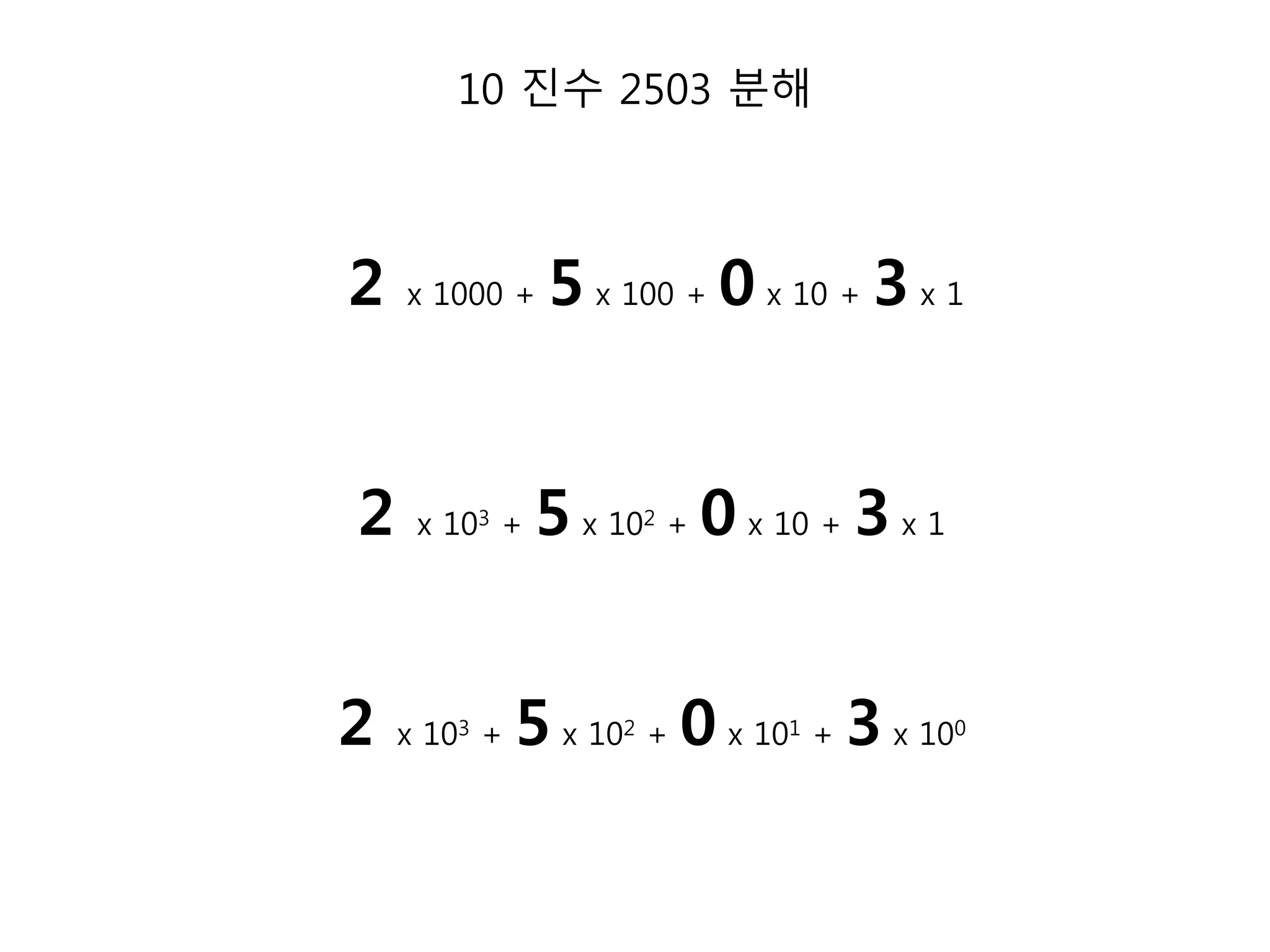
7. 10 진수 2503 분해
2 5 0 3
2는 ‘1000의 개수’를 나타냄
5는 ‘100의 개수’를 나타냄
0은 ’10의 개수’를 나타냄
3은 ‘1의 개수’를 나타냄

8. 10 진수 2503 분해
2 x 1000 + 5 x 100 + 0 x 10 + 3 x 1
2 x 103 + 5 x 102 + 0 x 10 + 3 x 1
2 x 103 + 5 x 102 + 0 x 101 + 3 x 100

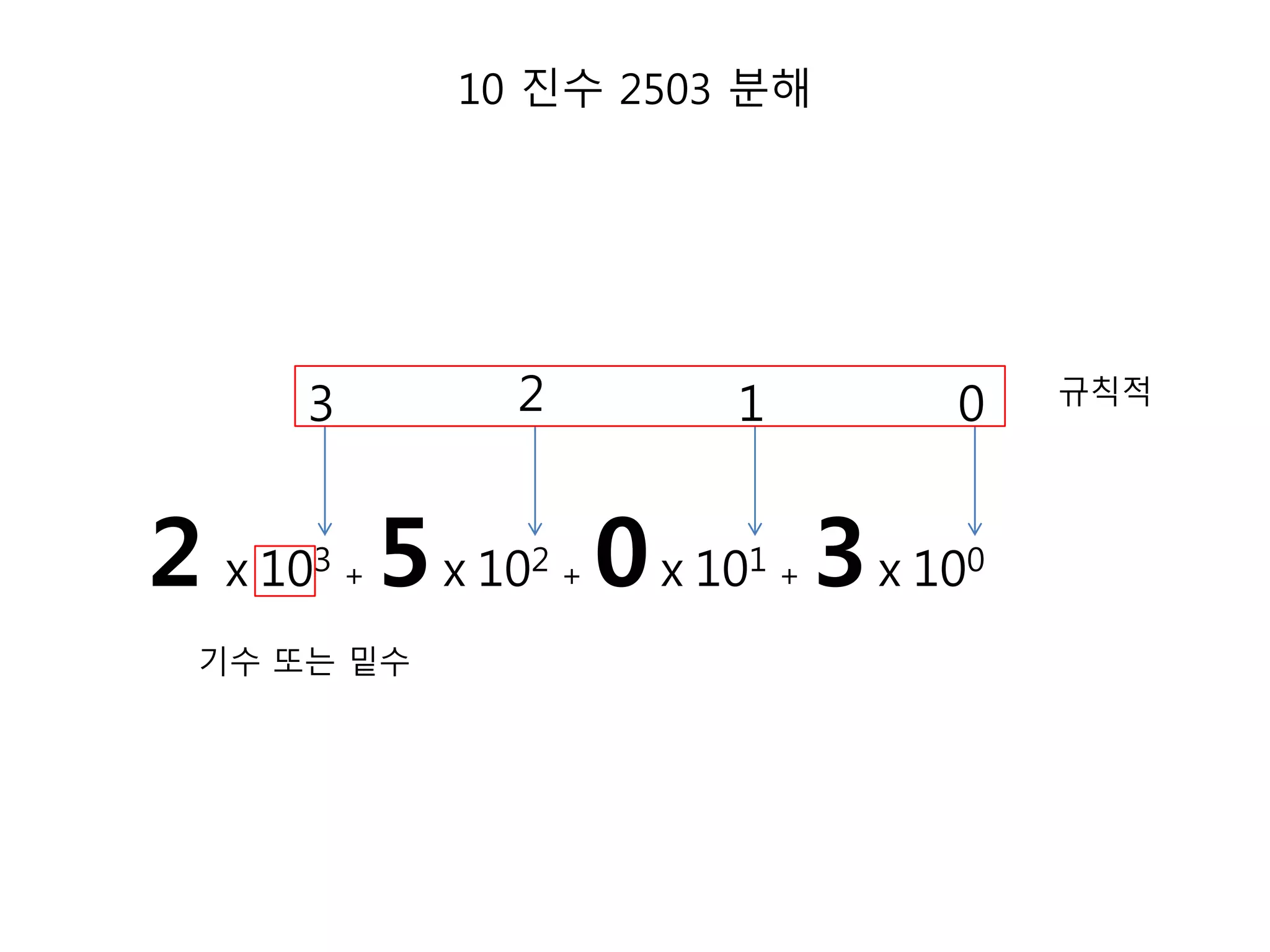
9. 10 진수 2503 분해
3 2 1 0 규칙적
2 x 103 + 5x 102 + 0x 101 + 3x 100
기수 또는 밑수

10. • 사용하는 숫자 : 0, 1  2종류
2 진법
• 자릿수에 의미가 있으며 오른쪽 부터 1의자리, 2의자리, 4의 자리 자리로 표기

11. 2 진수 1100 분해
1 1 0 0
1는 ‘8의 개수’를 나타냄
1는 ‘4의 개수’를 나타냄
0은 ’2의 개수’를 나타냄
0은 ‘1의 개수’를 나타냄

12. 2 진수 1100 분해
1 x 23 + 1x 22 + 0x 21 + 0x 20

13. 2 진법으로 쓴 1100 을 10진법으로 변환
1 x 23 + 1 x 22 + 0 x 21 + 0 x 20
= 1 x 8 + 1 x 4 + 0 x 2 + 0 x 1
= 8 + 4 + 0 + 0
= 12

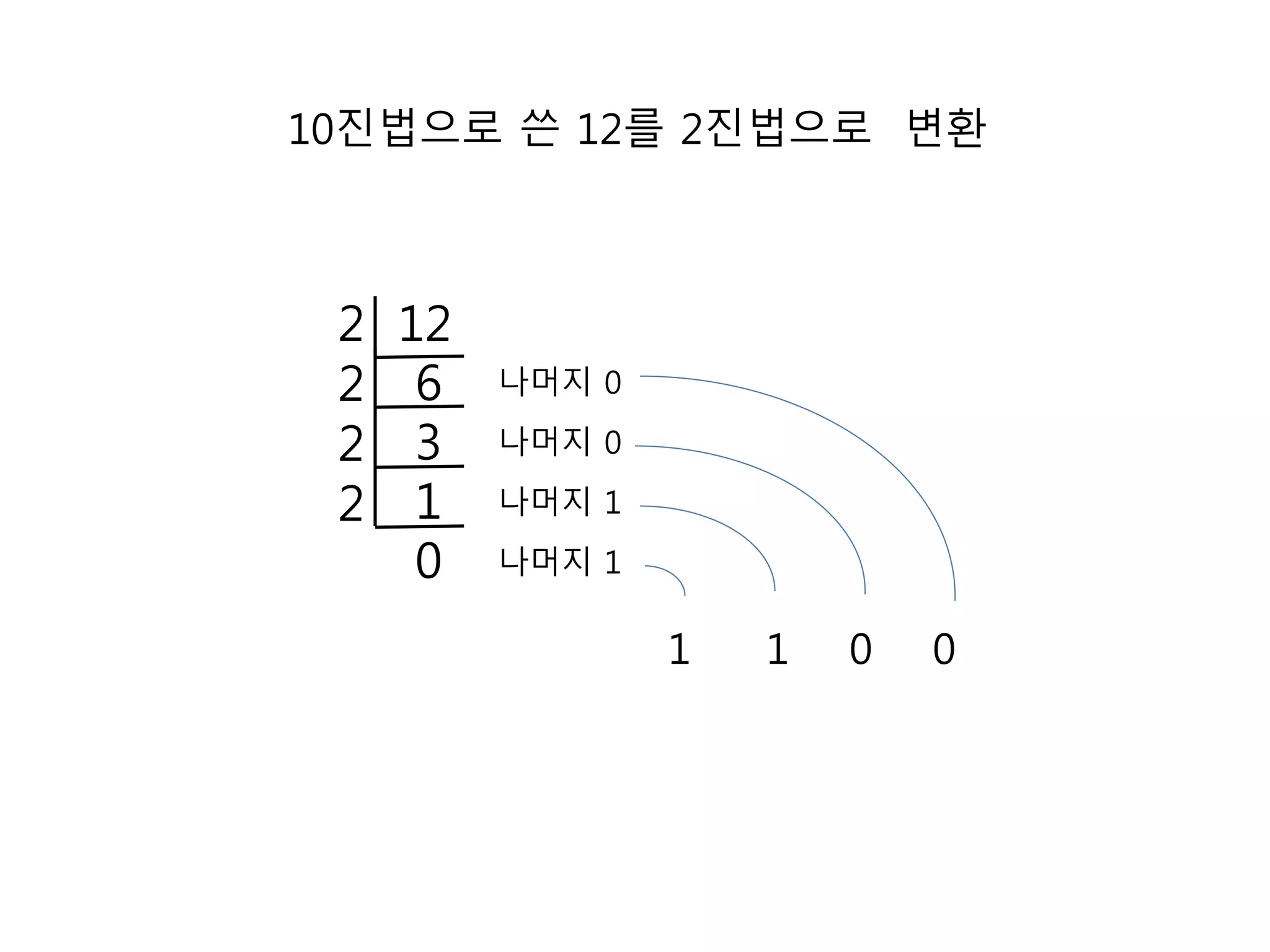
14. 10진법으로 쓴 12를 2진법으로 변환
12
6
3
1
0
2
2
2
2
나머지 0
나머지 0
나머지 1
나머지 1
1 1 0 0

15. 10진법으로 쓴 12를 2진법으로 변환
1 x 101 + 2 x 100
1 x 23 + 1 x 22 + 0 x 21 + 0 x 20
10진법은 밑수가 10이고 2진법은 밑수가 2가 됨
10진법 에서 2진법 표기 형식을 바꾸는 것을 진법변환(기수 교환) 이라고 함

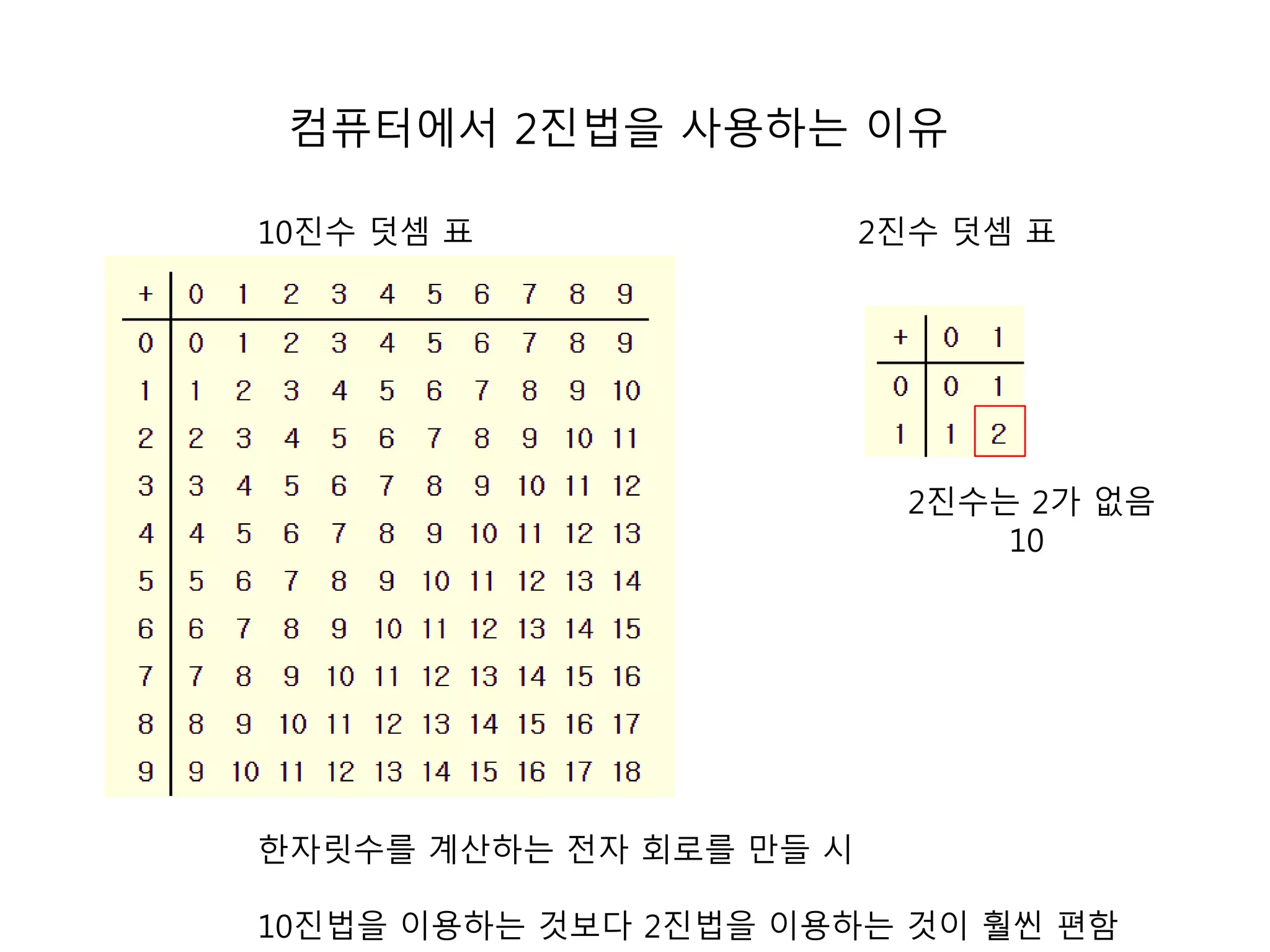
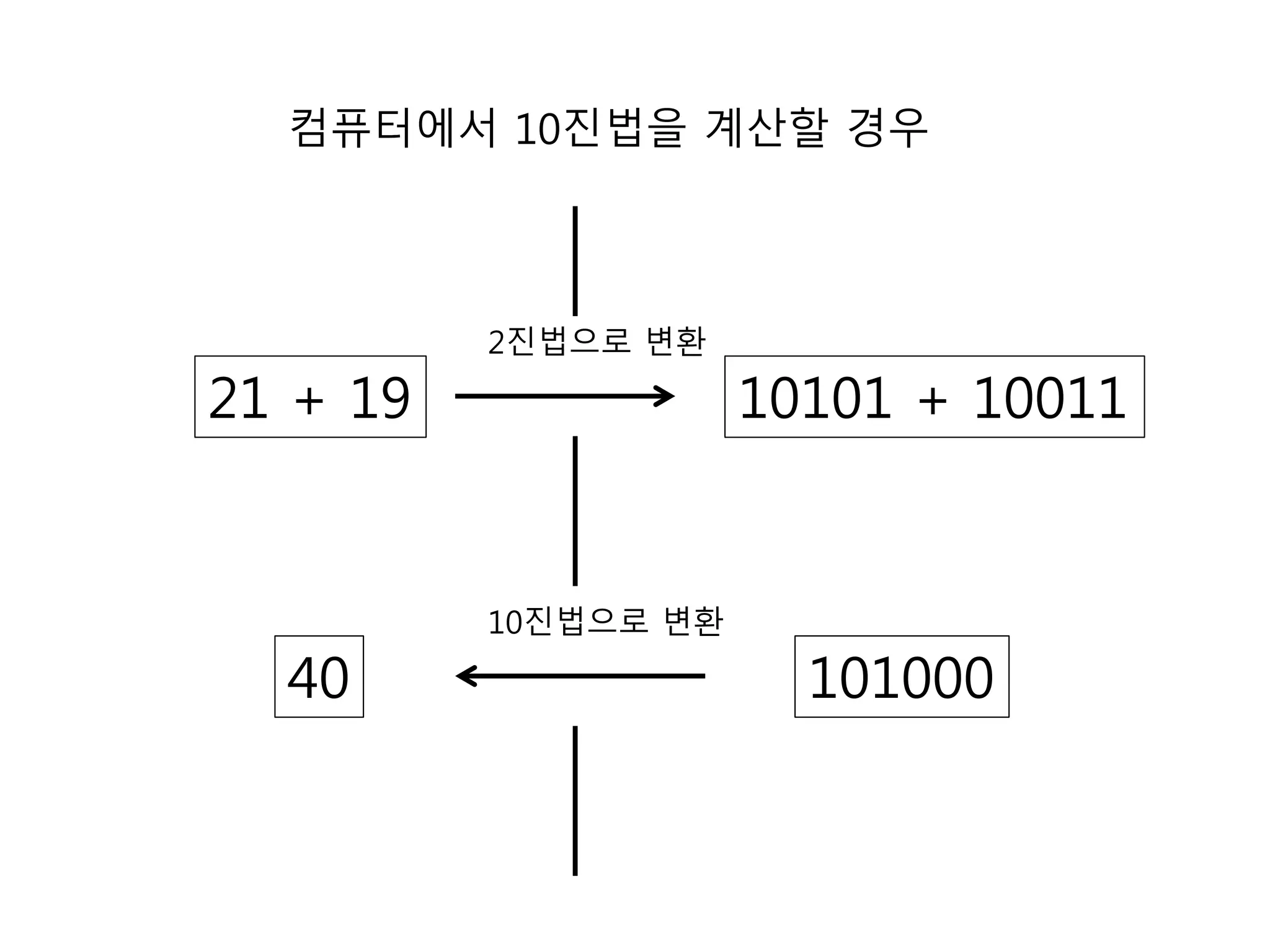
16. 컴퓨터에서 2진법을 사용하는 이유
10진수 덧셈 표 2진수 덧셈 표
2진수는 2가 없음
10
한자릿수를 계산하는 전자 회로를 만들 시
10진법을 이용하는 것보다 2진법을 이용하는 것이 훨씬 편함

17. 컴퓨터에서 2진법을 사용하는 이유
10진법 : 자릿수가 적어지지만, 숫자의 종류가 많아짐
2진법 : 숫자의 종류는 적지만, 자릿수가 많아짐

18. 컴퓨터에서 2진법을 사용하는 이유
사람 :
자릿수가 많으면 연산하기 어려움
컴퓨터 :
연산이 아주 빠르기 때문에 자릿수의 많고 적음이 없고
사람처럼 계산 실수를 하지 않음 따라서 계산 규칙이 간단한 것을 선호

19. 컴퓨터에서 10진법을 계산할 경우
2진법으로 변환
21 + 19 10101 + 10011
10진법으로 변환
40 101000

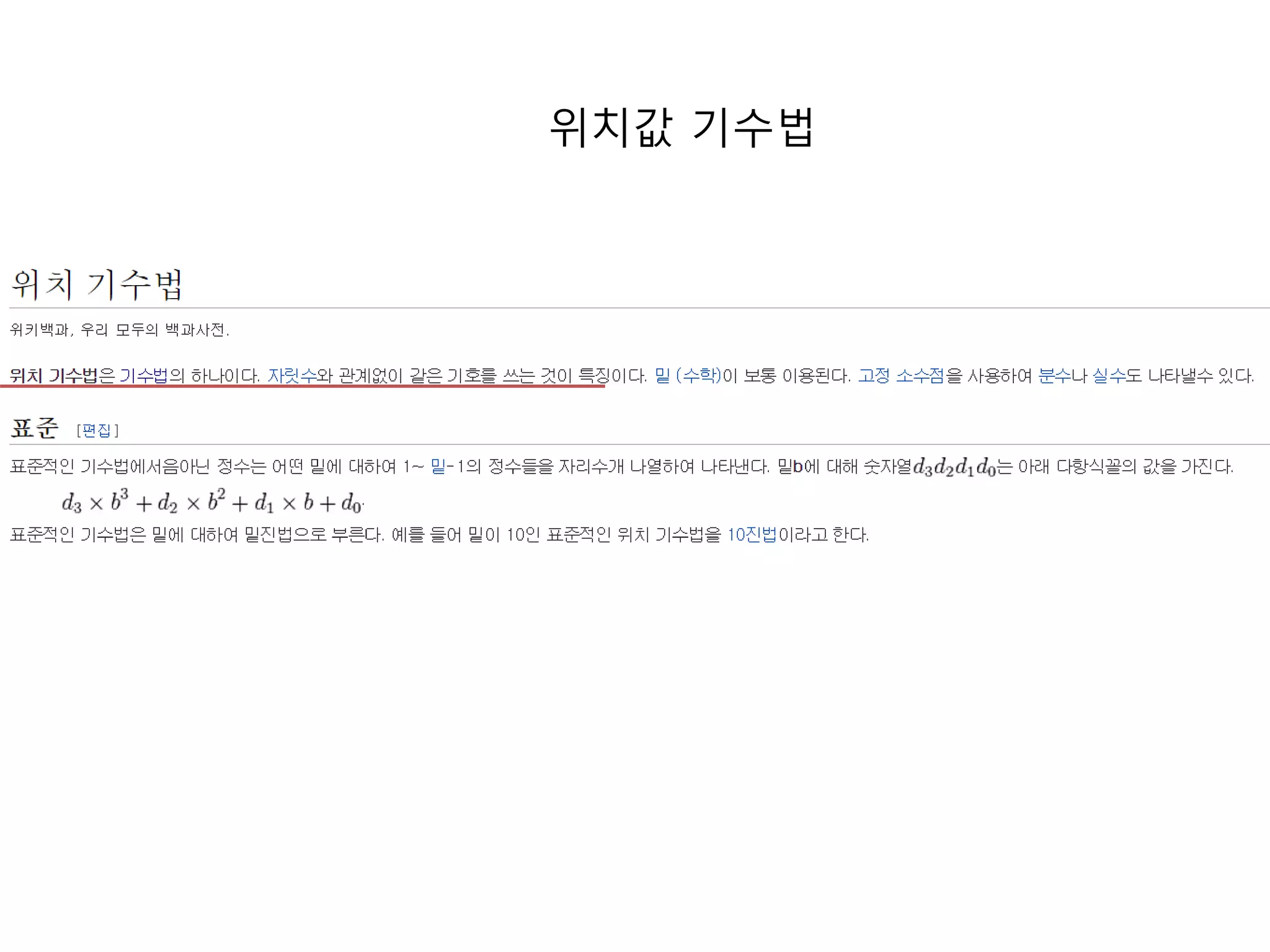
20. 위치값 기수법

21. 위치값 기수법을 사용하지 않는 로마 숫자
로마 숫자 표기법의 특징
숫자의 자리는 의미가 없으며 숫자 그 자체가 그 수를 나타냄
0이 없습니다.
Ⅰ(1), Ⅴ(5), Ⅹ(10), L(50), C(100), D(500), M(1000) 등의 문자를 사용
나열한 문자가 나타내는 수를 모두 더한 것이 전체 수가 됨

22. 위치값 기수법을 사용하지 않는 로마 숫자
로마 숫자 표기법 덧셈
Ⅲ + Ⅲ = ⅢⅢ (x)
Ⅲ + Ⅲ = Ⅵ (o)
(자릿수와는 무관)

23. ‘1은 100(10의 0승)’  100 = 1
지수법칙
‘102은 10을 2번 곱한 수’  100은 10을 0번 곱한 수  1이 아니라 0 이 아닌가????
100은 10을 0번 곱한 수라는 의미를 어떻게 해석해야 하는가?

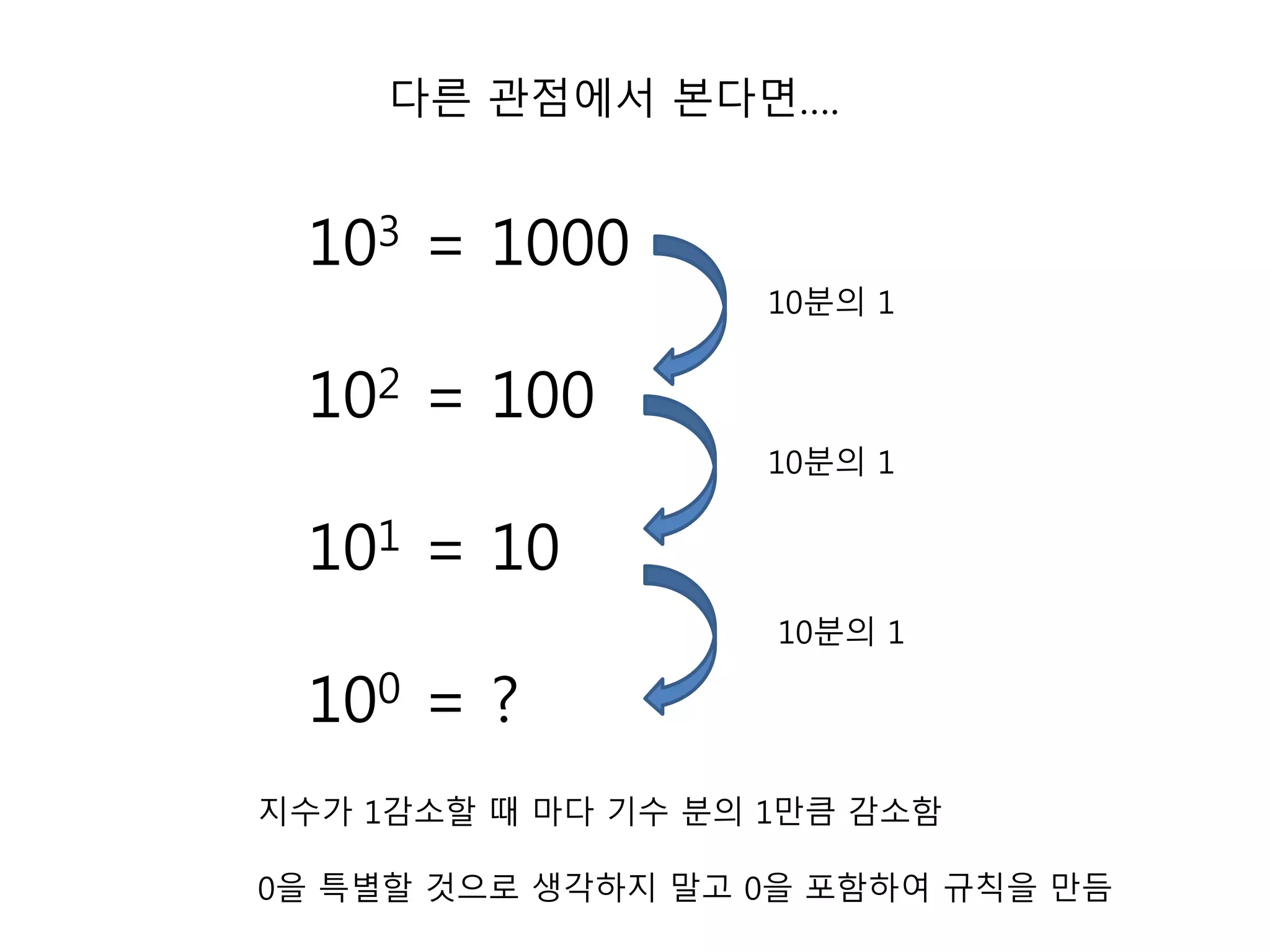
24. 다른 관점에서 본다면….
103 = 1000
102 = 100
101 = 10
100 = ?
10분의 1
10분의 1
10분의 1
지수가 1감소할 때 마다 기수 분의 1만큼 감소함
0을 특별할 것으로 생각하지 말고 0을 포함하여 규칙을 만듬

25. 다른 관점에서 본다면….
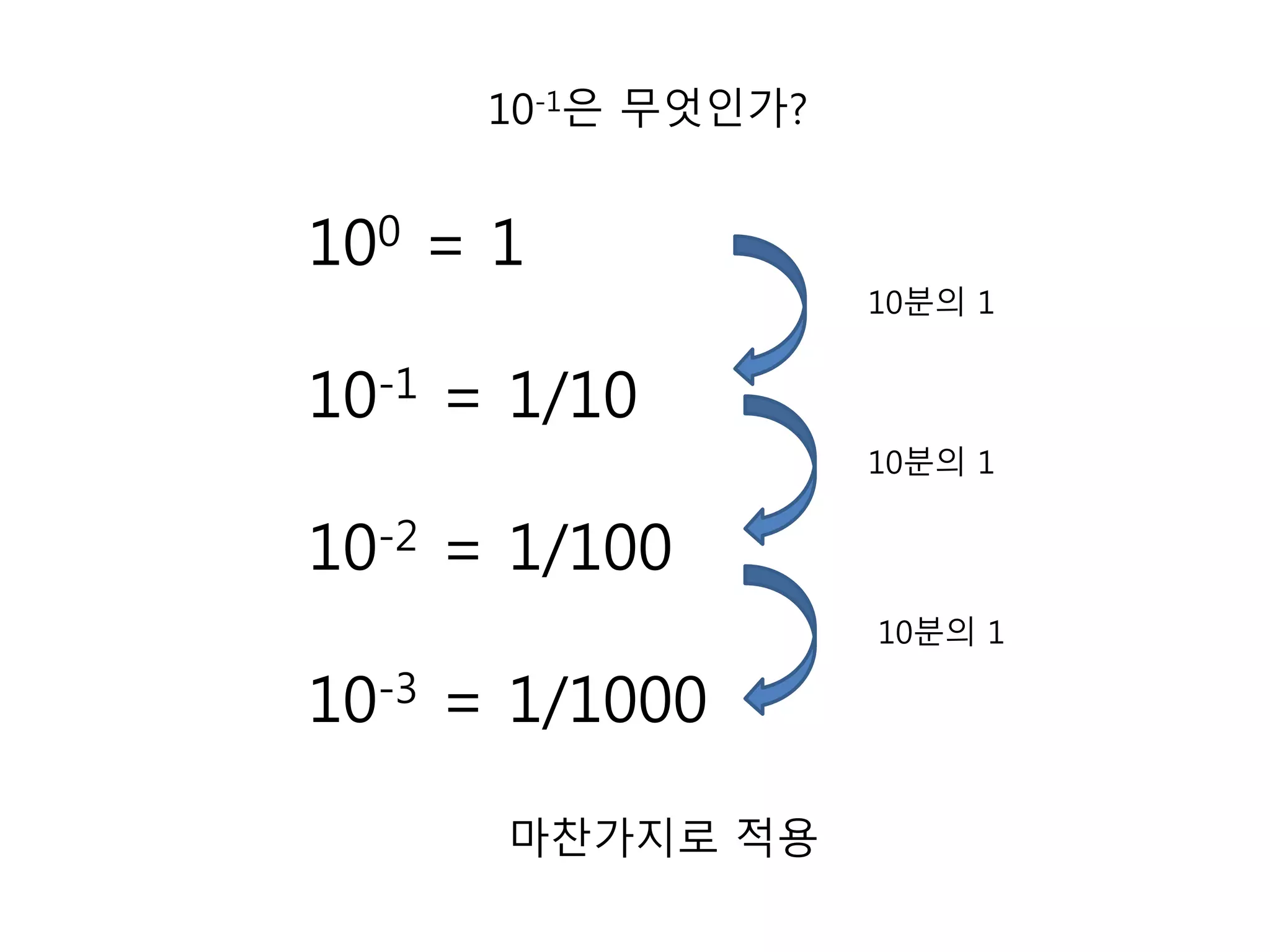
“지수가 1 줄어들면 전체는 밑수 분의 1이 된다”

26. 10-1은 무엇인가?
100 = 1
10-1 = 1/10
10-2 = 1/100
10-3 = 1/1000
10분의 1
10분의 1
10분의 1
마찬가지로 적용

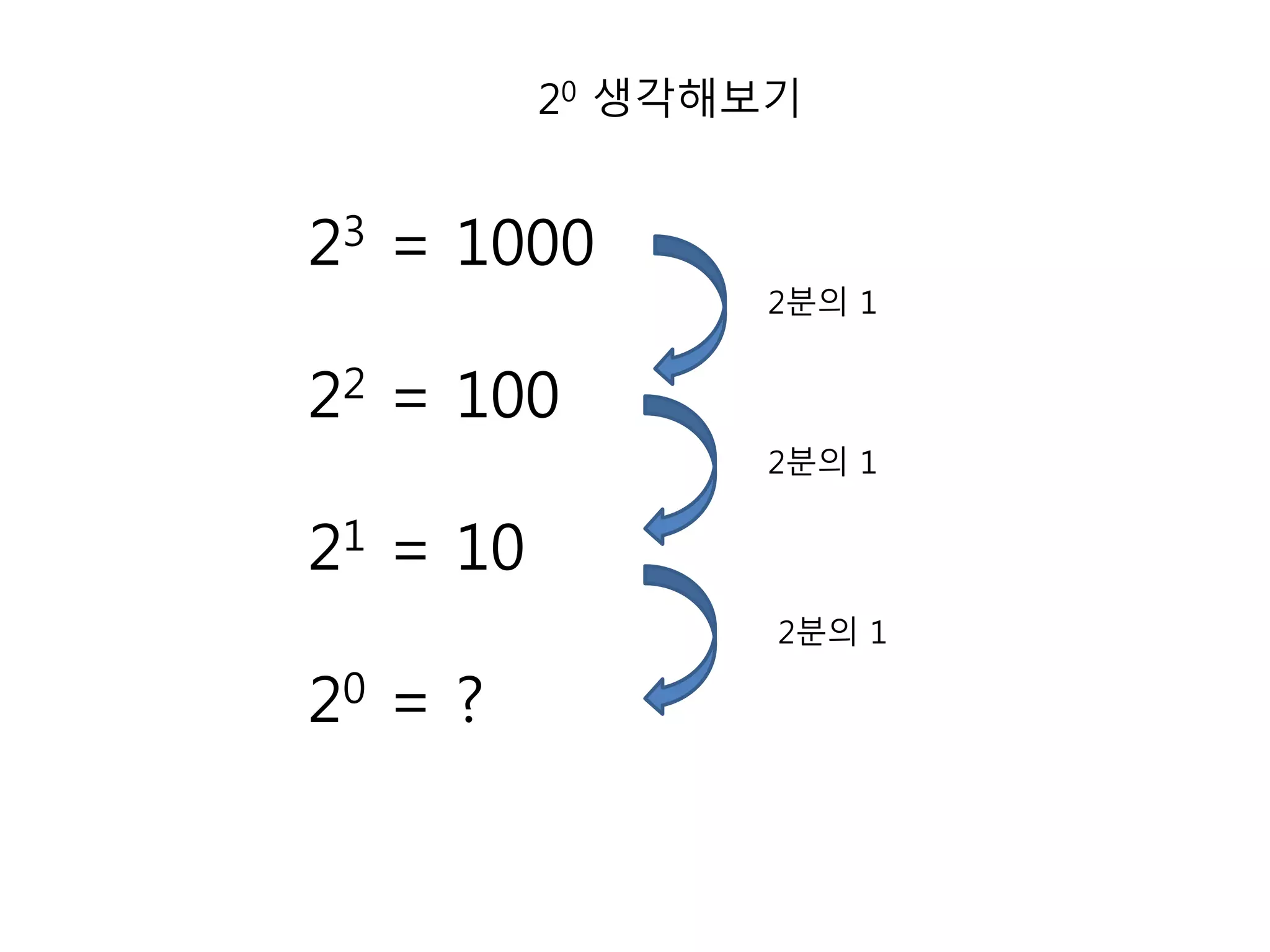
27. 20 생각해보기
23 = 1000
22 = 100
21 = 10
20 = ?
2분의 1
2분의 1
2분의 1

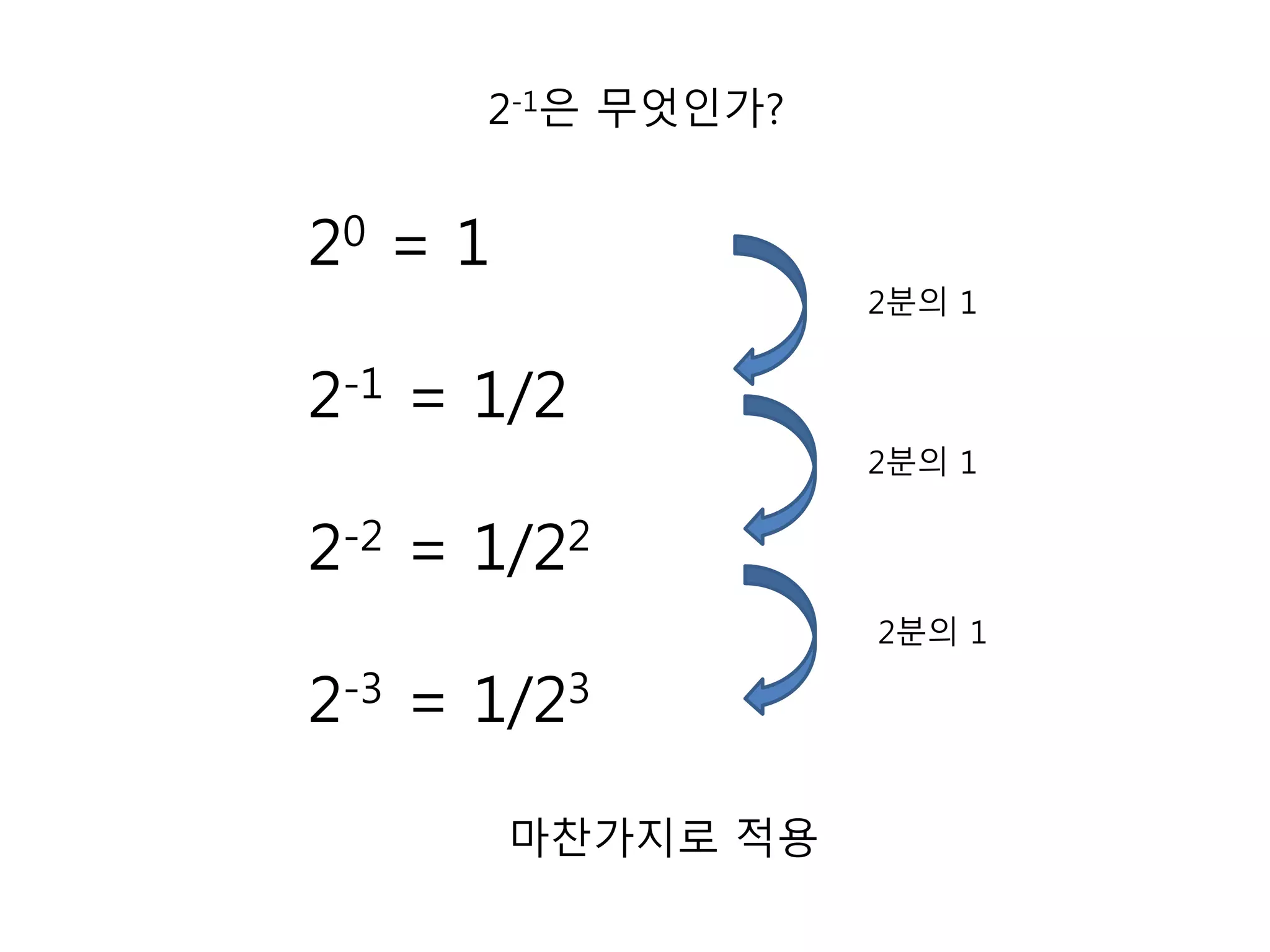
28. 2-1은 무엇인가?
20 = 1
2-1 = 1/2
2-2 = 1/22
2-3 = 1/23
2분의 1
2분의 1
2분의 1
마찬가지로 적용

29. 패턴 찾기
10+5 = 1 x 10 x 10 x 10 x 10 x 10
10+4 = 1 x 10 x 10 x 10 x 10
10+3 = 1 x 10 x 10 x 10
10+2 = 1 x 10 x 10
10+1 = 1 x 10
100 = 1
10-1 = 1 ÷ 10
10-2 = 1 ÷ 10 ÷ 10
10-3 = 1 ÷ 10 ÷ 10 ÷ 10
10-4 = 1 ÷ 10 ÷ 10 ÷ 10 ÷ 10
10-5 = 1 ÷ 10 ÷ 10 ÷ 10 ÷ 10 ÷ 10
2+5 = 1 x 2 x 2 x 2 x 2 x 2
2+4 = 1 x 2 x 2 x 2 x 2
2+3 = 1 x 2 x 2 x 2
2+2 = 1 x 2 x 2
2+1 = 1 x 2
20 = 1
2-1 = 1 ÷ 2
2-2 = 1 ÷ 2 ÷ 2
2-3 = 1 ÷ 2 ÷ 2 ÷ 2
2-4 = 1 ÷ 2 ÷ 2 ÷ 2 ÷ 2
2-5 = 1 ÷ 2 ÷ 2 ÷ 2 ÷ 2 ÷ 2
지수법칙 : Na x Nb = Na+b

30. 0의 역할
1) 자리확보
2) 패턴을 만들어 규칙을 간단하게 하기

31. 자리 확보
2 5 0 3 0을 생략 하면? 2 5 3

32. 자리 확보
위치값 기수법에서는 자리가 중요한 의미가 있으므로
10의 자릿수가 없어도 그곳에 무언가 숫자를 두어야 함
0의 역할은 자리를 확보하는 역할

33. 패턴을 만들어 규칙을 간단하게 하기
0을 사용하여 위치값 기수법의 각 자리의 크기를 10n 으로 통일해서 나타낼 수 있음
그렇지 않으면 1자리만 특별하게 취급해 다뤄야 함
0을 사용하면 패턴을 만들어내고 그 패턴을 이용하여 식을 표현할 수 있게 됨

34. 인간의 한계
10000000000000 과 1000000000000 중 어느 값이 더 큰가???
위치값 표기법으론 바로 알기가 쉽지 않음
1013 과 1012 으론 쉽기 알 수 있음  지수 표기법을 사용

35. End