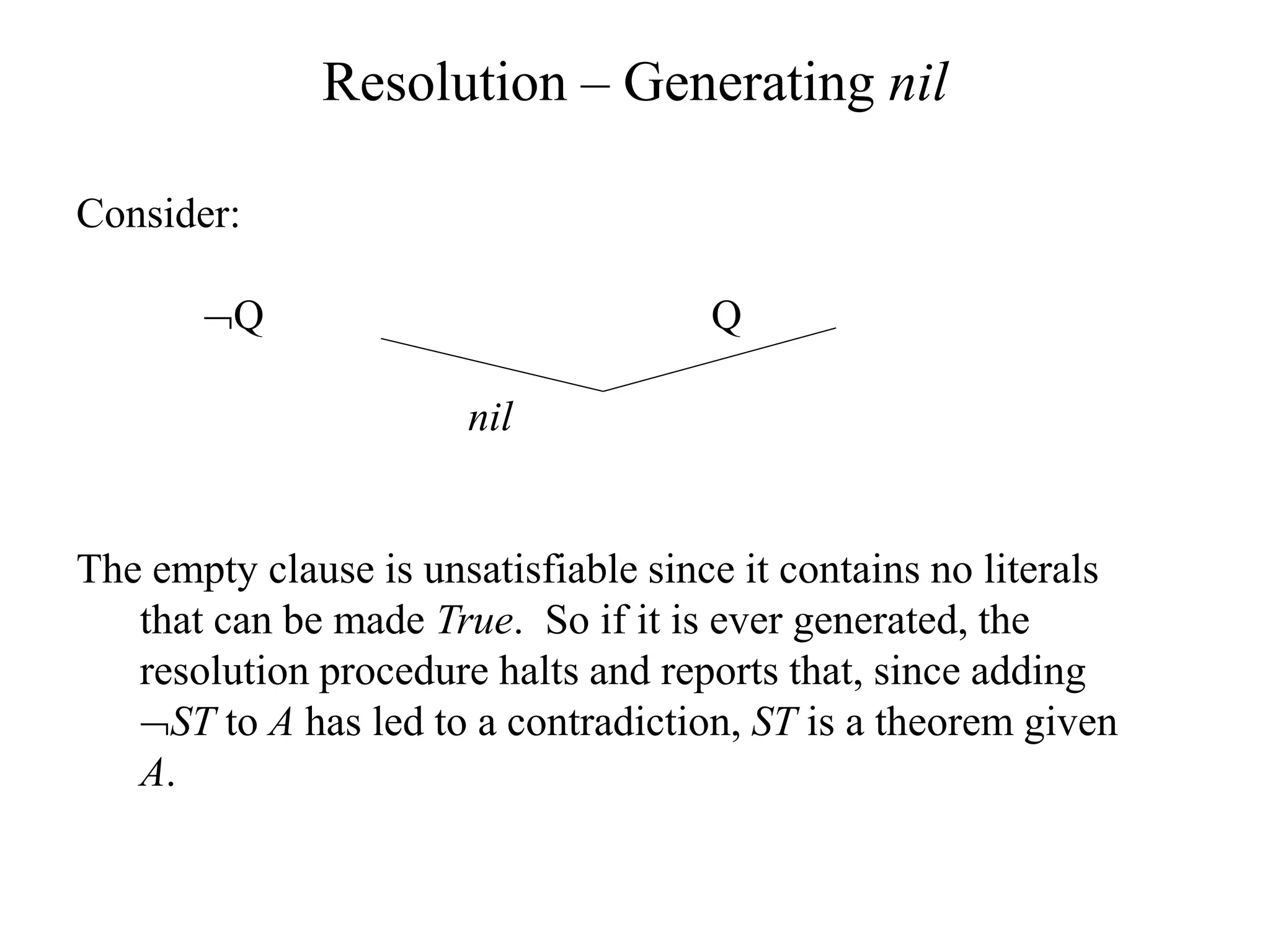
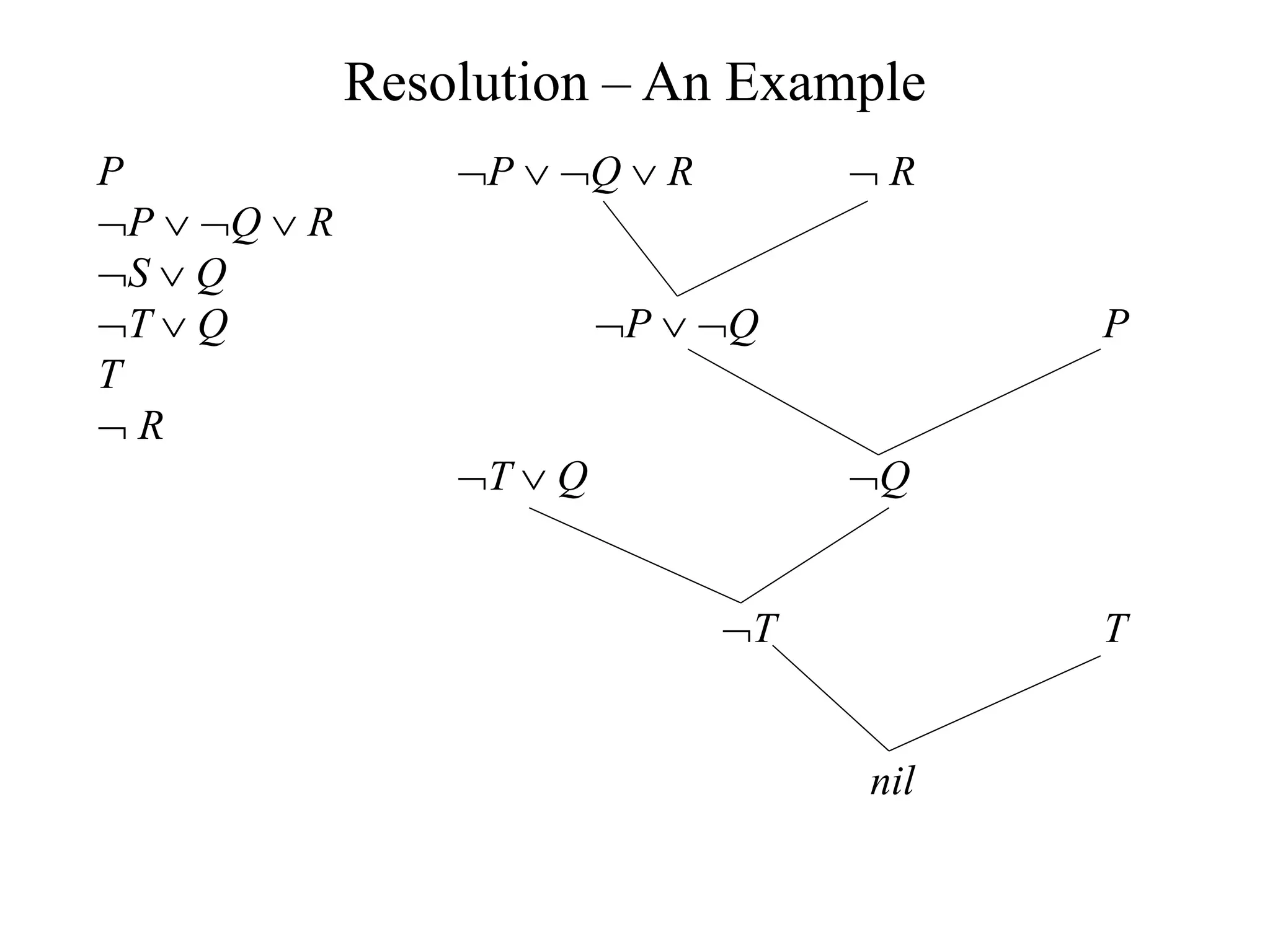
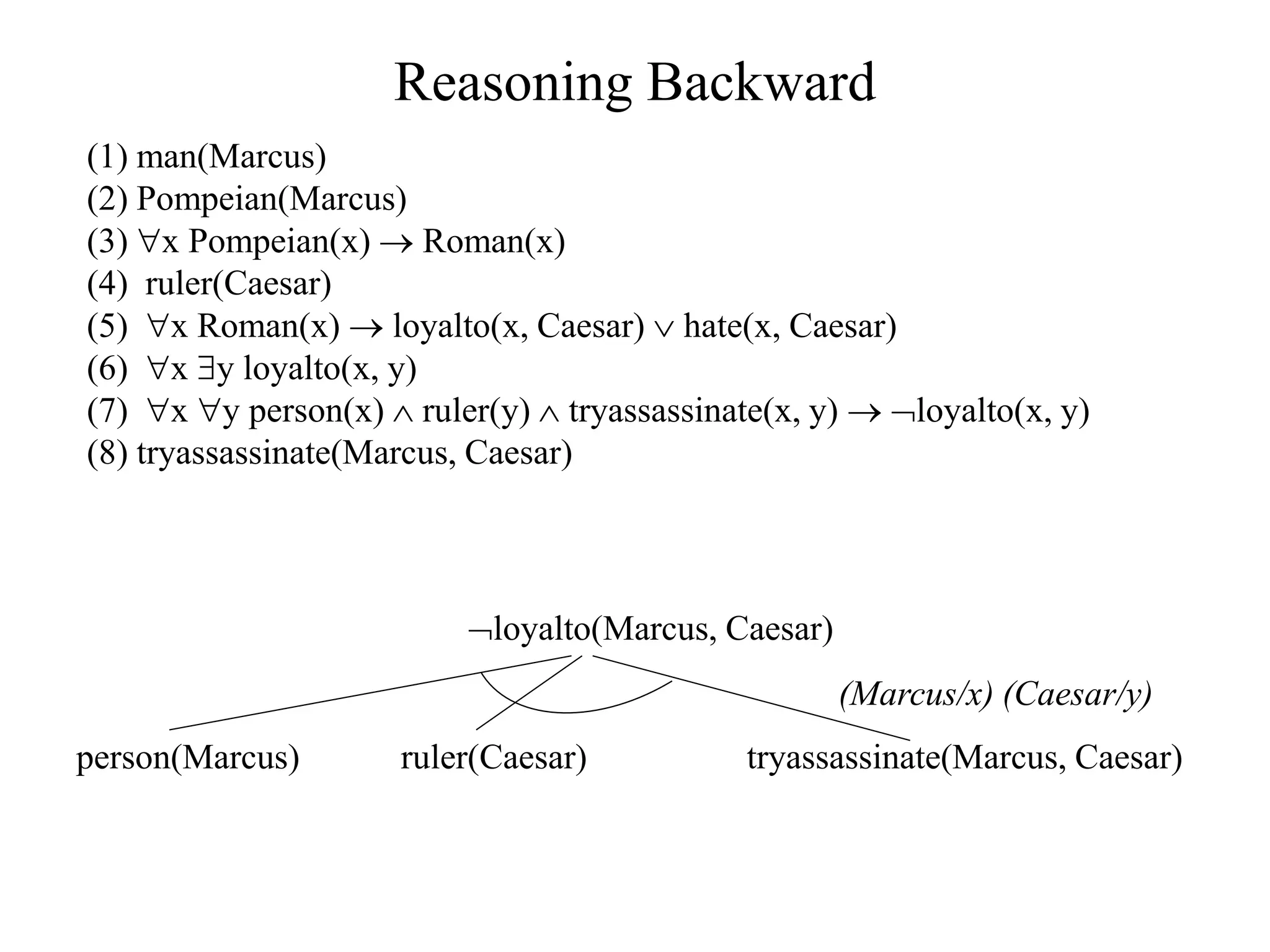
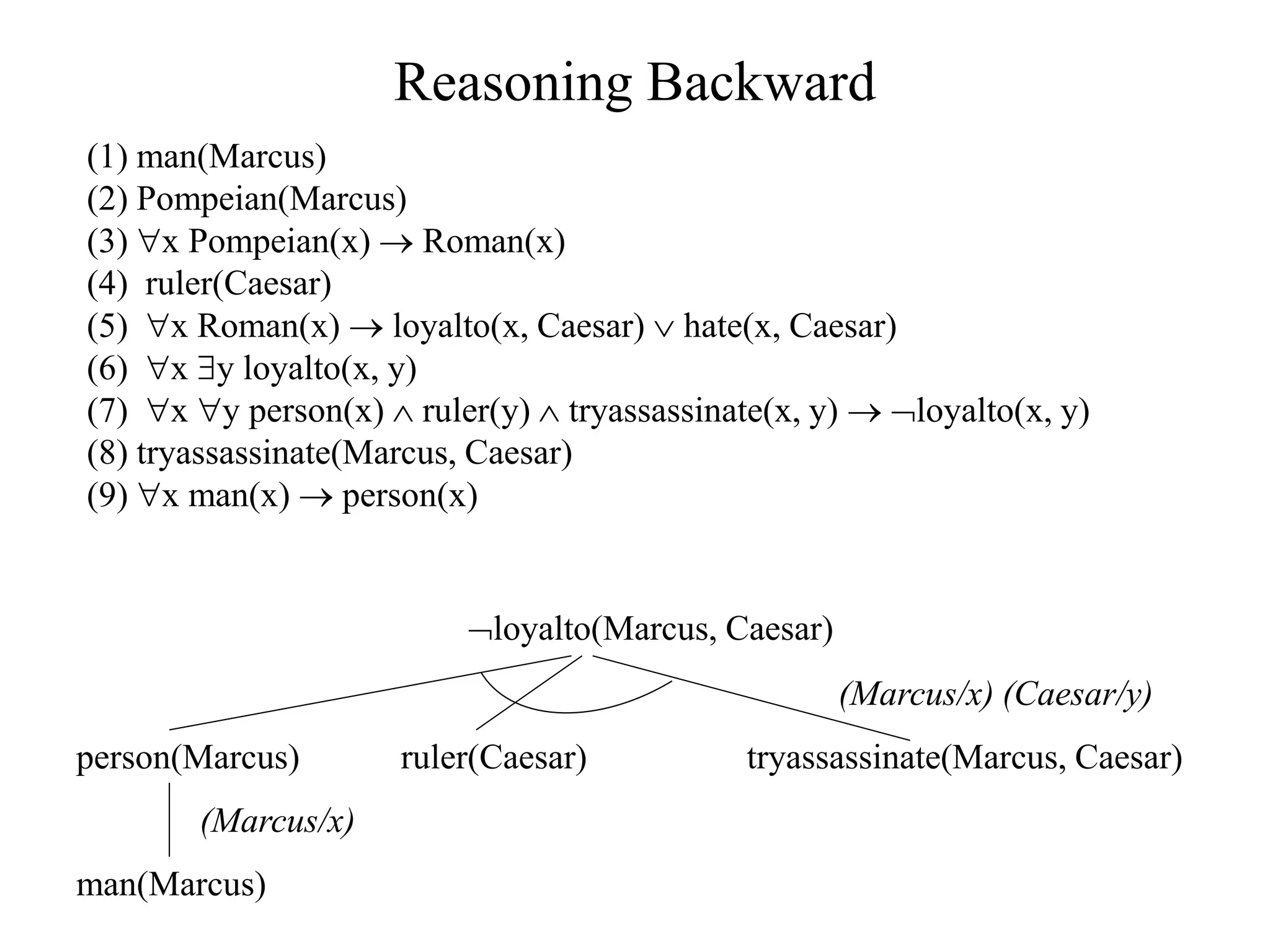
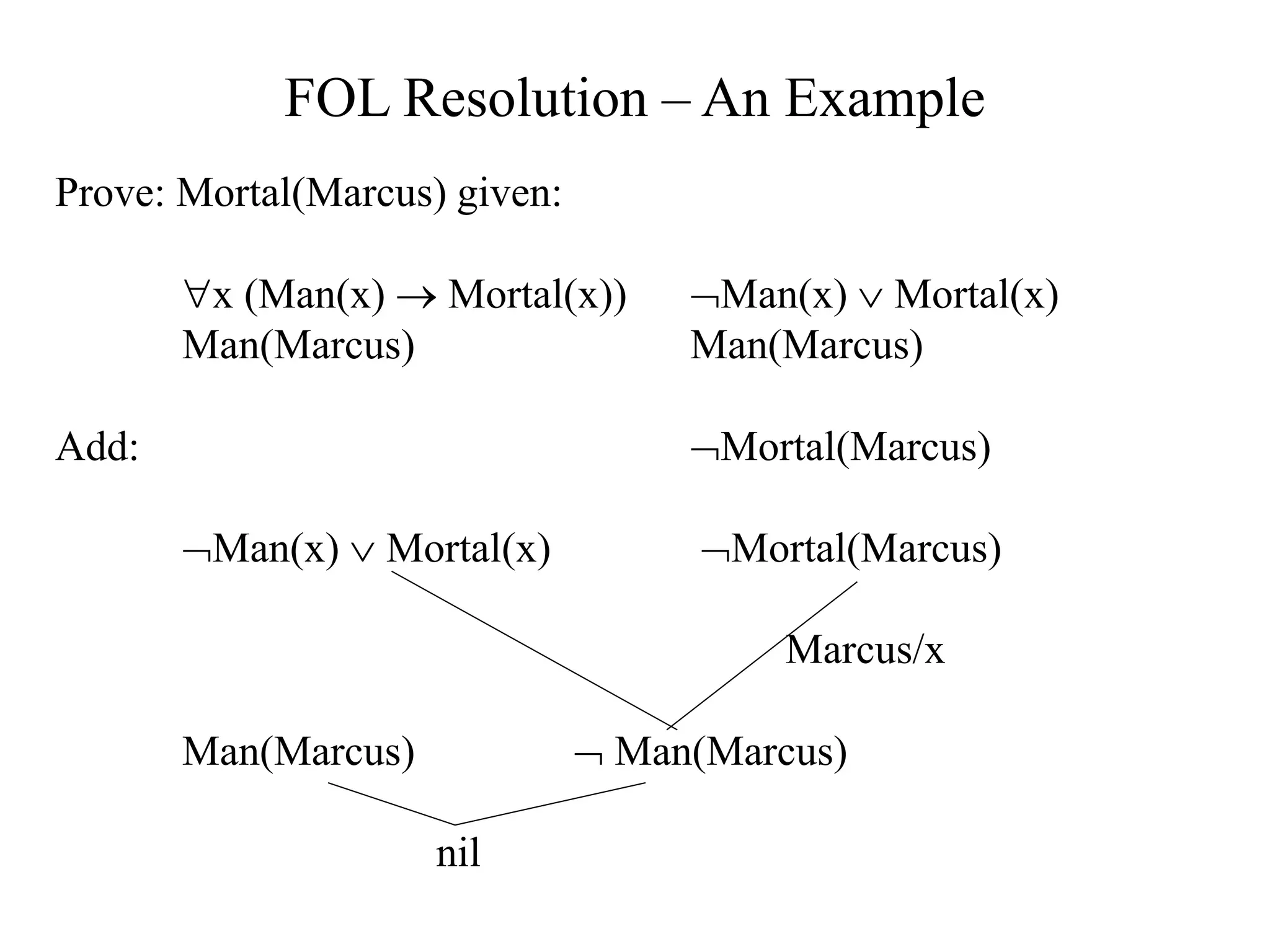
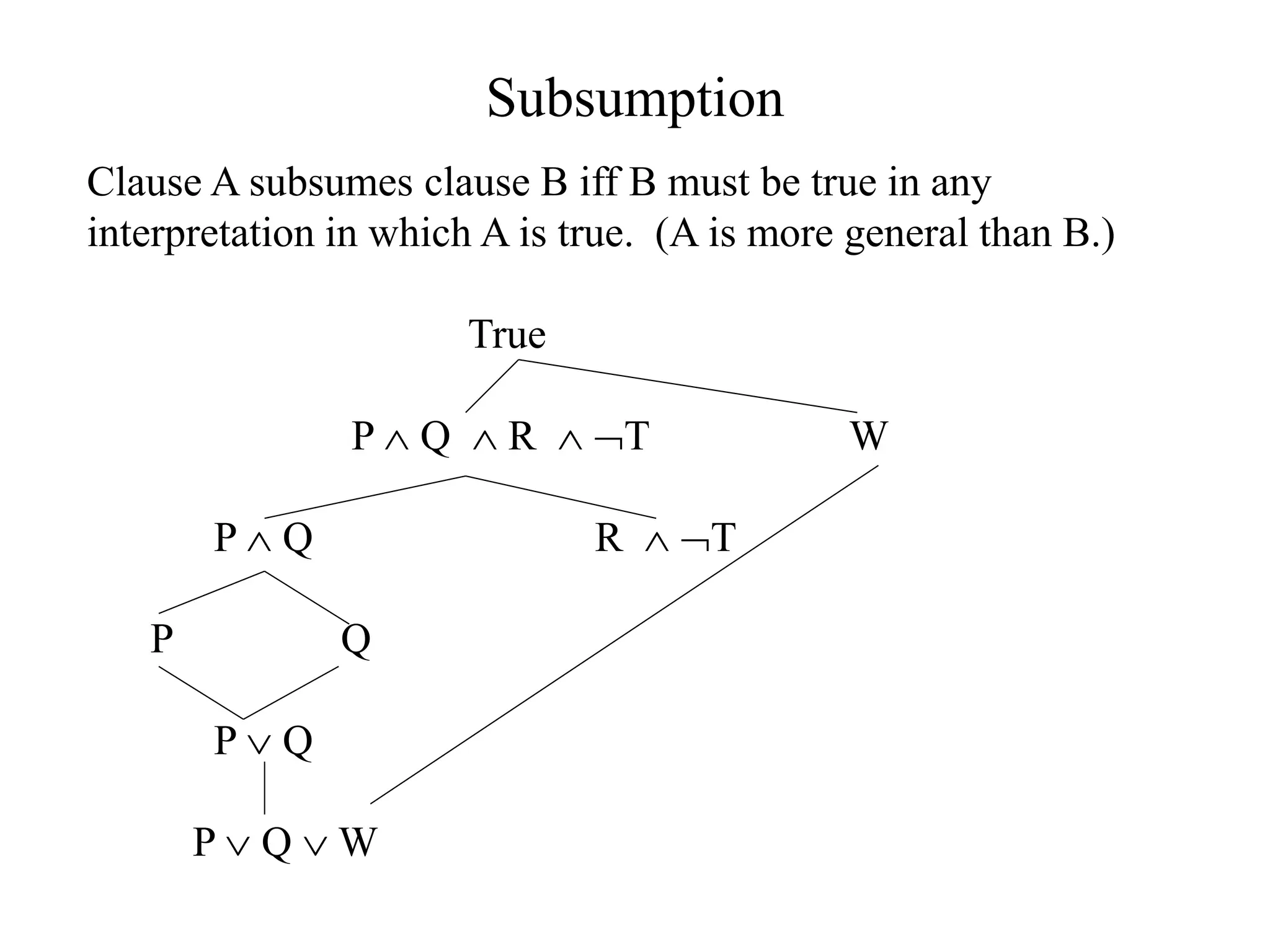
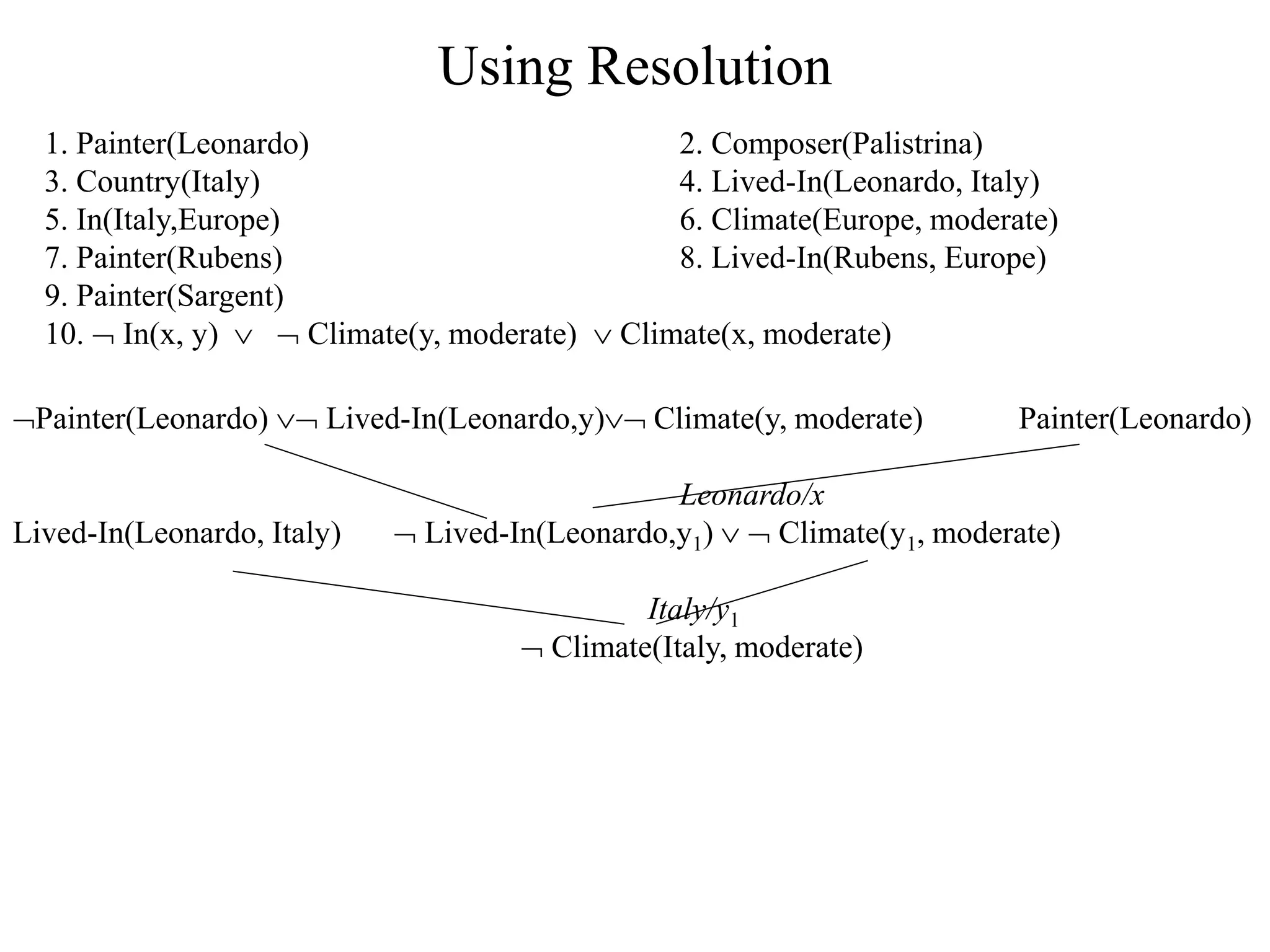
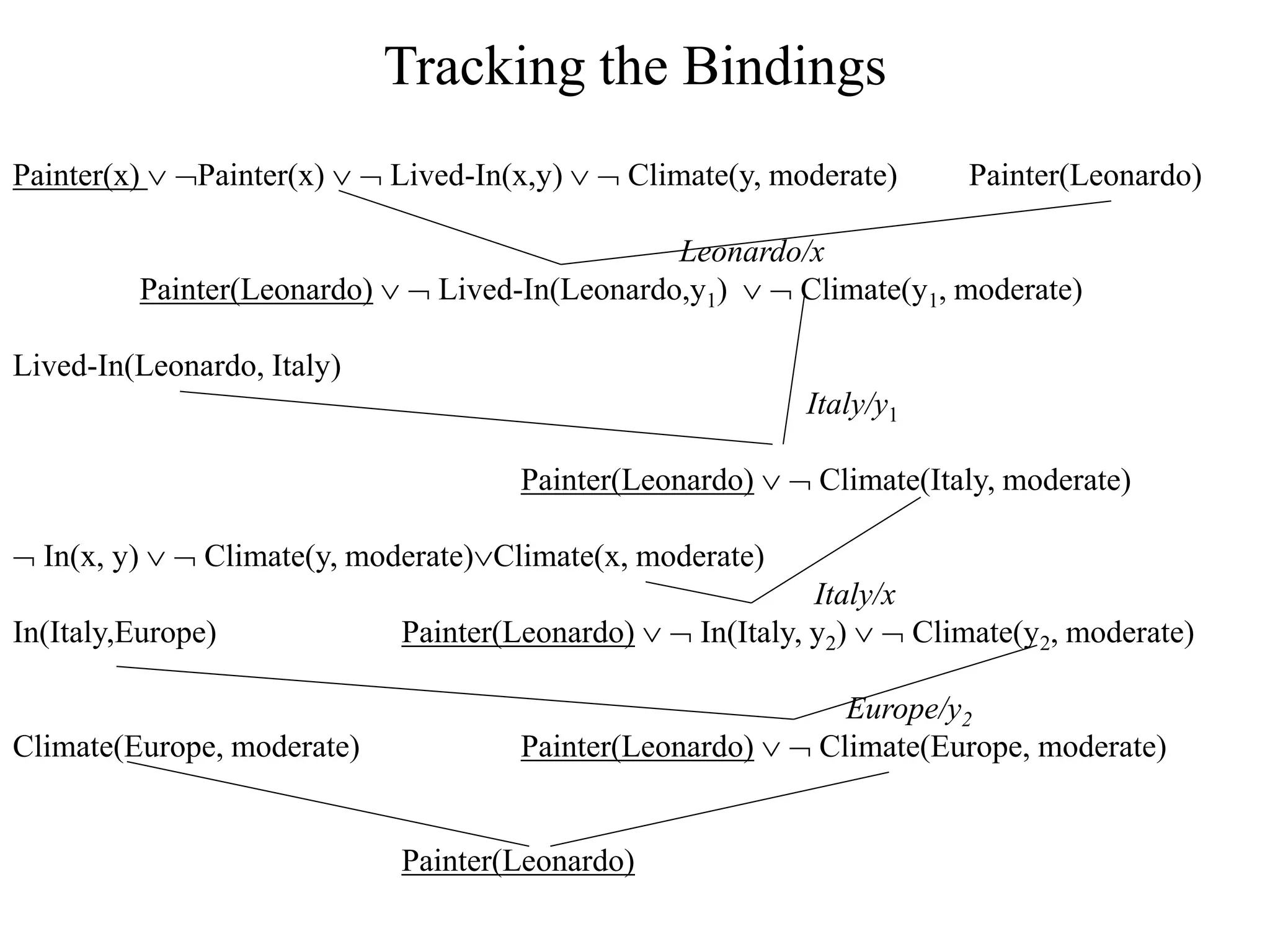
The document discusses logical representations and resolution. It begins by covering Boolean logic and conjunctive normal form (CNF). It defines literals, clauses, and well-formed formulas (wffs) in CNF. It then proves that every wff can be converted to an equivalent wff in CNF. The document provides an example of this conversion. It also discusses resolution, which allows deducing new facts by resolving clauses based on complementary literals. Resolution is used to determine logical entailment and prove theorems. An example of using resolution to prove a statement is also provided.



















![A Harder One
Given:
x [Roman(x) know(x, Marcus)]
[hate(x, Caesar) (y (z hate(y, z)) thinkcrazy(x, y))]
Roman(Isaac)
hate(Isaac, Caesar)
hate(Paulus, Marcus)
thinkcrazy(Isaac, Paulus)
Prove:
know(Isaac, Marcus)](https://image.slidesharecdn.com/ch8-logicalrepresentationandreasoning-240108161546-01079ab3/75/Ch8-LogicalRepresentationAndReasoning-ppt-24-2048.jpg)


![Clause Form Simplifies the Process
x [Roman(x) know(x, Marcus)]
[hate(x, Caesar) (y (z hate(y, z)) thinkcrazy(x, y))]
becomes:
Roman(x) know(x, Marcus) hate(x, Caesar) hate(y, z)
thinkcrazy(x, y)](https://image.slidesharecdn.com/ch8-logicalrepresentationandreasoning-240108161546-01079ab3/75/Ch8-LogicalRepresentationAndReasoning-ppt-27-2048.jpg)
![Conversion to Clause Form - Step 1
1. Eliminate , using the fact that a b is equivalent to
a b
x [Roman(x) know(x, Marcus)]
[hate(x, Caesar) (y (z hate(y, z)) thinkcrazy(x, y))]
x [Roman(x) know(x, Marcus)]
[hate(x, Caesar) (y (z hate(y, z)) thinkcrazy(x, y))]](https://image.slidesharecdn.com/ch8-logicalrepresentationandreasoning-240108161546-01079ab3/75/Ch8-LogicalRepresentationAndReasoning-ppt-28-2048.jpg)
![Conversion to Clause Form - Step 2
2. Reduce the scope of each to a single term, using:
•(p) = p
•deMorgan’s laws
•x P(x) x P(x)
•x P(x) x P(x)
x [Roman(x) know(x, Marcus)]
[hate(x, Caesar) (y (z hate(y, z)) thinkcrazy(x, y))]
x [ Roman(x) know(x, Marcus)]
[hate(x, Caesar) (y z hate(y, z) thinkcrazy(x, y))]](https://image.slidesharecdn.com/ch8-logicalrepresentationandreasoning-240108161546-01079ab3/75/Ch8-LogicalRepresentationAndReasoning-ppt-29-2048.jpg)

![Conversion to Clause Form - Step 4
4. Move all quantifiers to the left without changing their relative
order.
x [ Roman(x) know(x, Marcus)]
[hate(x, Caesar) (y z hate(y, z) thinkcrazy(x, y))]
x y z [ Roman(x) know(x, Marcus)]
[hate(x, Caesar) ( hate(y, z) thinkcrazy(x, y))]
At this point, we have prenex normal form.](https://image.slidesharecdn.com/ch8-logicalrepresentationandreasoning-240108161546-01079ab3/75/Ch8-LogicalRepresentationAndReasoning-ppt-31-2048.jpg)

![Conversion to Clause Form - Step 6
6. Drop the prefix since all remaining quantifiers are universal.
x y z [ Roman(x) know(x, Marcus)]
[hate(x, Caesar) ( hate(y, z) thinkcrazy(x, y))]
[ Roman(x) know(x, Marcus)]
[hate(x, Caesar) ( hate(y, z) thinkcrazy(x, y))]](https://image.slidesharecdn.com/ch8-logicalrepresentationandreasoning-240108161546-01079ab3/75/Ch8-LogicalRepresentationAndReasoning-ppt-33-2048.jpg)
![Conversion to Clause Form - Step 7
7. Convert the matrix into a conjunction of disjuncts by using:
•Associative properties of and .
[ Roman(x) know(x, Marcus)]
[hate(x, Caesar) ( hate(y, z) thinkcrazy(x, y))]
Roman(x) know(x, Marcus)
hate(x, Caesar) hate(y, z) thinkcrazy(x, y)
•Distributivity of and .
(P(x) Q(x)) T(x)
(P(x) T(x)) (Q(x)) T(x))](https://image.slidesharecdn.com/ch8-logicalrepresentationandreasoning-240108161546-01079ab3/75/Ch8-LogicalRepresentationAndReasoning-ppt-34-2048.jpg)










![Unification Examples
Inputs
[1] Roman(x),
Roman(Paulus)
[2] Roman(x),
Ancient(Paulus)
[3] Roman(father-of(Marcus)),
Roman(x)
[4] Roman(father-of(Marcus)),
Roman(Flavius),
[5] Roman(x),
Roman(y),
[6] Roman(father-of(x)),
Roman(x)
[7] Likes(x, y),
Likes(Flavius, Marcus)
Result
Succeed
Fail
Succeed
Fail
Succeed
Fail (fails occur
check)
Succeed
Substitution
Paulus/x
father-of(Marcus)/x
x/y
Flavius/x, Marcus/y](https://image.slidesharecdn.com/ch8-logicalrepresentationandreasoning-240108161546-01079ab3/75/Ch8-LogicalRepresentationAndReasoning-ppt-45-2048.jpg)









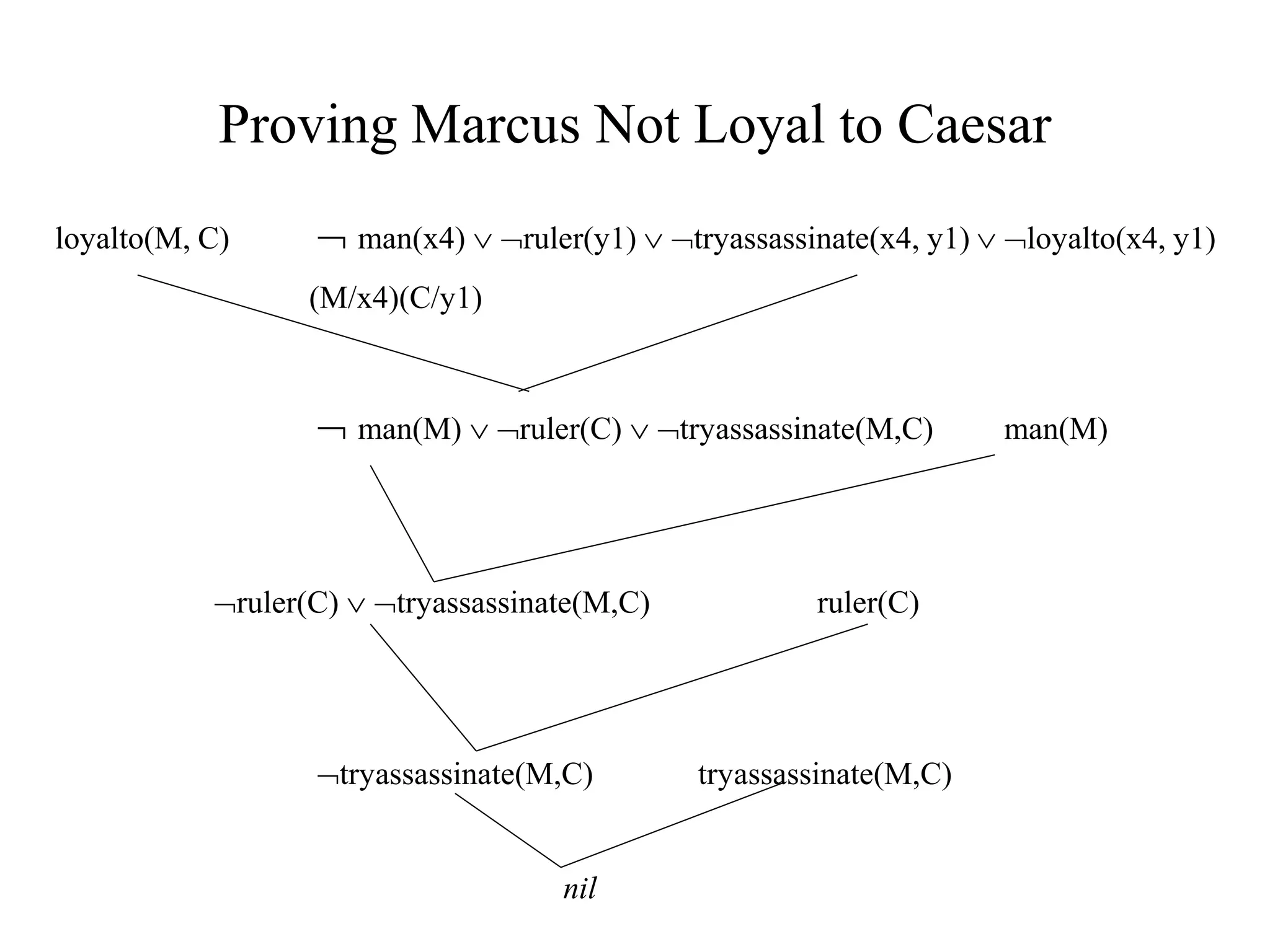
![Does Isaac Know Marcus?
Given:
1. x [Roman(x) know(x, Marcus)]
[hate(x, Caesar) (y (z hate(y, z)) thinkcrazy(x, y))]
Roman(x) know(x, Marcus) hate(x, Caesar)
hate(y, z) thinkcrazy(x, y)
2. Roman(Isaac)
3. hate(Isaac, Caesar)
4. hate(Paulus, Marcus)
5. thinkcrazy(Isaac, Paulus)
Prove:
know(Isaac, Marcus) * know(Isaac, Marcus)](https://image.slidesharecdn.com/ch8-logicalrepresentationandreasoning-240108161546-01079ab3/75/Ch8-LogicalRepresentationAndReasoning-ppt-60-2048.jpg)






