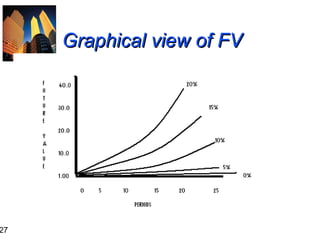
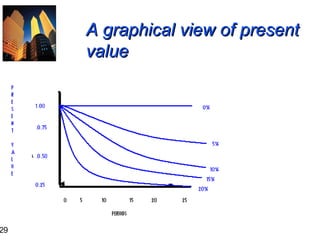
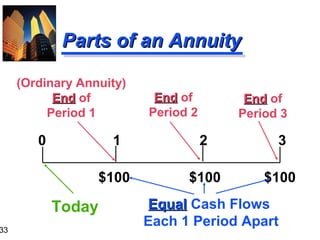
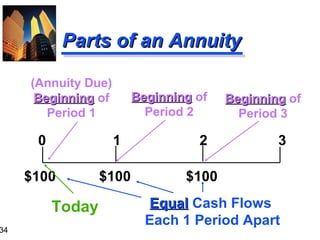
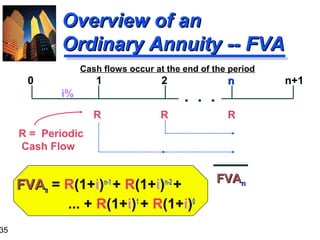
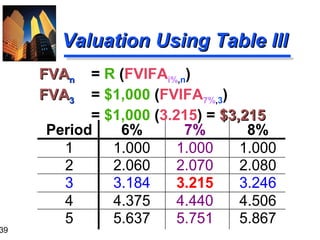
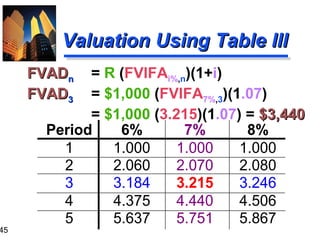
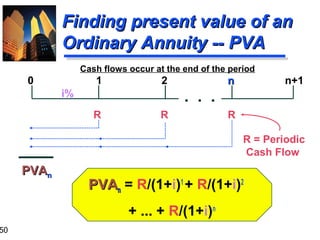
1. The document discusses the concepts of time value of money, interest rates, and different types of interest including simple and compound interest. 2. It provides formulas for calculating future value and present value using simple and compound interest, and examples of applying these formulas. 3. The document also covers annuities, explaining the differences between ordinary annuities and annuities due. It provides formulas and examples for calculating future and present value of both types of annuities.

1. 1
Chapter 3
Time Value of
Money

2. 2
The Time Value of Money
The Interest Rate
Simple Interest
Compound Interest
Amortizing a Loan

3. 3
The Interest Rate
Which would you prefer -- $10,000 today or $10,000 in 5 years?
years
Interest is the money paid for the use of money.
Obviously, $10,000 today.
today
You already recognize that there is TIME VALUE TO MONEY!!
MONEY

4. 4
Why TIME?
Why is TIME such an important
element in your decision?
TIME allows you the opportunity to
postpone consumption and earn
INTEREST.
INTEREST

5. 5
Types of Interest
Simple Interest
Interest paid (earned) on only the original
amount, or principal borrowed (lend).
Compound Interest
Interest paid (earned) on any previous
interest earned, as well as on the
principal borrowed (lent).

6. 6
Simple Interest Formula
Formula
SI = P0(i)(n)
SI:
Simple Interest
P0:
Deposit today (t=0)
i:
Interest Rate per Period
n:
Number of Time Periods

7. 7
Simple Interest Example
Assume that you deposit $1,00 in an
account earning 8% simple interest for
10 years. What is the accumulated
interest at the end of the 10nd year?
SI
= P0(i)(n)
= $1,00(.08)(10)
= $80

8. 8
Simple Interest (FV)
What is the Future Value (FV) of the
FV
deposit?
FV
= P0 + SI
= $1,00 + $80
= $180
Future Value is the value at some future
time of a present amount of money, or a
series of payments, evaluated at a given
interest rate.

9. 9
Simple Interest (PV)
What is the Present Value (PV) of the
PV
previous problem?
The Present Value is simply the
$1,00 you originally deposited.
That is the value today!
Present Value is the current value of a
future amount of money, or a series of
payments, evaluated at a given interest
rate.

10. 10
Compound interest
Interest that is earned on a given
deposit and has become part of
principal at the end of a specified
period
Future value of a present amount at a
future date, found by applying
compound interest over a specified
period of time.

11. 11
The equation for future value
FV=PV*(1+i)n
If Fred places $100 in a savings account paying 8% interest compounded
annually, at the end of 1 year he will have $108 in the
account.<100*(1.08)=$108>
If Fred were to leave this money in the account for another year, he would
be paid interest at the rate of 8% on the new principal of $108.At the end of
this second year there would be $116.64 in the
account.<108*(1.08)=116.64> or <100*(1.08)2=116.64>

12. 12
General Future
Value Formula
FV1 = P0(1+i)1
FV2 = P0(1+i)2
etc.
General Future Value Formula:
FVn = P0 (1+i)n
or
FVn = P0 (FVIFi,n) -- See Table I

13. 13
Valuation Using Table I
FVIFi,n is found on Table I at the end
of the book or on the card insert.
Period
1
2
3
4
5
6%
1.060
1.124
1.191
1.262
1.338
7%
1.070
1.145
1.225
1.311
1.403
8%
1.080
1.166
1.260
1.360
1.469

14. 14
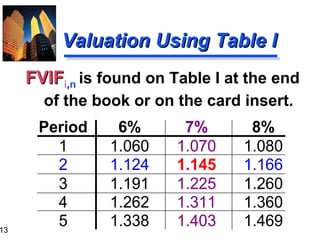
Using Future Value Tables
FV2
= $1,000 (FVIF7%,2)
= $1,000 (1.145)
= $1,145 [Due to Rounding]
Period
6%
7%
8%
1
1.060
1.070
1.080
2
1.124
1.145
1.166
3
1.191
1.225
1.260
4
1.262
1.311
1.360
5
1.338
1.403
1.469

15. 15
Story Problem Example
Julie Miller wants to know how large her deposit
of $10,000 today will become at a compound
annual interest rate of 10% for 5 years.
years
0
10%
1
2
3
4
5
$10,000
FV5

16. 16
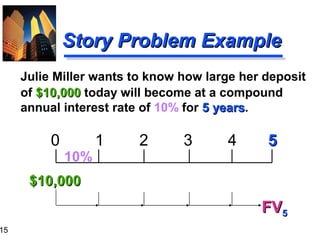
Story Problem Solution
Calculation based on general formula:
FVn = P0 (1+i)n
FV5 = $10,000 (1+ 0.10)5
= $16,105.10
Calculation based on Table I:
FV5 = $10,000 (FVIF10%, 5)
= $10,000 (1.611)
= $16,110 [Due to Rounding]

17. 17
Present value of a single
amount
The current dollar value of a
future amount-the amount of
money that would have to be
invested today at a given interest
rate over a specified period to
equal the future amount.

18. 18
Concept of present value
The process of finding present
value is often referred to as
discounting cash flows. It is
concerned with answering the following
question:" if I can earn i percent on my
money, what is the most I would be willing
to pay now for an opportunity to receive
FV n dollars n periods from today?”

19. 19
Equation for calculating PV
PV*(1+i)n=FV
PV=FV/(1+i)n

20. 20
Present Value
Single Deposit (Graphic)
Assume that you need $1,000 in 2 years.
Let’s examine the process to determine
how much you need to deposit today at a
discount rate of 7% compounded
annually.
0
7%
1
2
$1,000
PV0
PV1

21. 21
Present Value
Single Deposit (Formula)
PV0 = FV2 / (1+i)2
= $1,000 / (1.07)2
= FV2 / (1+i)2
= $873.44
0
7%
1
2
$1,000
PV0

22. 22
General Present
Value Formula
PV0 = FV1 / (1+i)1
PV0 = FV2 / (1+i)2
etc.
General Present Value Formula:
PV0 = FVn / (1+i)n
or
PV0 = FVn (PVIFi,n) -- See Table II

23. 23
Valuation Using Table II
PVIFi,n is found on Table II at the end
of the book or on the card insert.
Period
1
2
3
4
5
6%
.943
.890
.840
.792
.747
7%
.935
.873
.816
.763
.713
8%
.926
.857
.794
.735
.681

24. 24
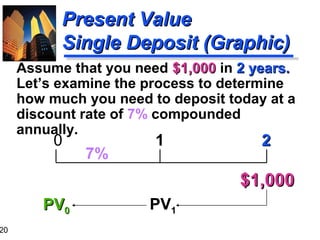
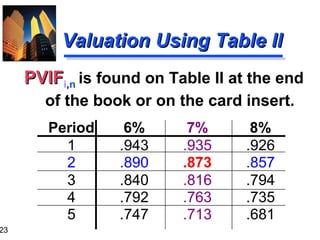
Using Present Value Tables
PV2
= $1,000 (PVIF7%,2)
= $1,000 (.873)
= $873 [Due to Rounding]
Period
6%
7%
1
.943
.935
2
.890
.873
3
.840
.816
4
.792
.763
5
.747
.713
8%
.926
.857
.794
.735
.681

25. 25
Story Problem Example
Julie Miller wants to know how large of a
deposit to make so that the money will
grow to $10,000 in 5 years at a discount
rate of 10%.
0
10%
1
2
3
4
5
$10,000
PV0

26. 26
Story Problem Solution
Calculation based on general formula:
PV0 = FVn / (1+i)n
PV0 = $10,000 / (1+ 0.10)5
= $6,209.21
Calculation based on Table I:
PV0 = $10,000 (PVIF10%, 5)
= $10,000 (.621)
= $6,210.00 [Due to Rounding]

27. 27
Graphical view of FV
GRAPHICAL VIEW OF FV

28. 28
Future value relationship
Higher the interest rates, higher the
future value
Longer the period of time, higher the
future value
For an interest rate of 0% the FV is
always equal to its PV(1.00). But for
any interest rate greater than zero,
future value is greater than the
present value

29. 29
A graphical view of present
value

30. 30
Present value relationship
The higher the discount rate, the
lower the present value
The longer the period of time, the
lower the present value
At the discount rate 0%,the
present value is always equal to
its future value

31. 31
Types of Annuities
An Annuity represents a series of equal
payments (or receipts) occurring over a
specified number of equidistant periods.
Ordinary Annuity: Payments or receipts
Annuity
occur at the end of each period.
Annuity Due: Payments or receipts
Due
occur at the beginning of each period.

32. 32
Examples of Annuities
Student Loan Payments
Car Loan Payments
Insurance Premiums
Mortgage Payments
Retirement Savings

33. 33
Parts of an Annuity
(Ordinary Annuity)
End of
Period 1
0
End of
Period 2
End of
Period 3
1
2
3
$100
$100
$100
Today
Equal Cash Flows
Each 1 Period Apart

34. 34
Parts of an Annuity
(Annuity Due)
Beginning of
Period 1
Beginning of
Period 2
0
1
2
$100
$100
Beginning of
Period 3
$100
Today
3
Equal Cash Flows
Each 1 Period Apart

35. 35
Overview of an
Ordinary Annuity -- FVA
Cash flows occur at the end of the period
0
1
2
n
. . .
i%
R
R
R
R = Periodic
Cash Flow
FVAn = R(1+i) + R(1+i) +
... + R(1+i)1 + R(1+i)0
n-1
n-2
FVAn
n+1

36. 36
Example of an
Ordinary Annuity -- FVA
Cash flows occur at the end of the period
0
1
2
3
$1,000
$1,000
4
$1,000
7%
$1,070
$1,145
FVA3 = $1,000(1.07)2 +
$1,000(1.07)1 + $1,000(1.07)0
= $1,145 + $1,070 + $1,000
= $3,215
$3,215 = FVA3

37. 37
Future value interest factor
for an ordinary annuity
FVIFi,n=1/i*<(1+i)n-1>
FVA=PMT*(FVIFAi,n)

38. 38
Hint on Annuity Valuation
The future value of an ordinary
annuity can be viewed as
occurring at the end of the last
cash flow period, whereas the
future value of an annuity due
can be viewed as occurring at
the beginning of the last cash
flow period.

39. 39
Valuation Using Table III
FVAn
FVA3
= R (FVIFAi%,n)
= $1,000 (FVIFA7%,3)
= $1,000 (3.215) = $3,215
Period
6%
7%
8%
1
1.000
1.000
1.000
2
2.060
2.070
2.080
3
3.184
3.215
3.246
4
4.375
4.440
4.506
5
5.637
5.751
5.867

40. 40
Overview View of an
Annuity Due -- FVAD
Cash flows occur at the beginning of the period
0
1
2
3
R
R
R
i%
R
. . .
FVADn = R(1+i)n + R(1+i)n-1 +
... + R(1+i)2 + R(1+i)1
= FVAn (1+i)
n-1
n
R
FVADn

41. 41
numerical
Martin has $10000 that she can deposit in any of three
saving counts for a 3 year period. Bank A compounds
interest on an annual basis, bank B compounds interest
twice each year, Bank C compounds interest each quarter.
All three banks have a stated annual interest rate of 4%
What amount would Ms.Martin have at the end of third
year?
On the basis of your findings in banks, which bank should
she prefer.

42. 42
NUMERICALS
Ramish wishes to choose the better of two equally costly cash
flow streams: annuity X and annuity Y.X is an annuity due with a
cash inflow of $9000 for each of 6 years is an ordinary annuity
with cash inflow of 410000 or each of 6 years. Assume that he can
earn 15% on his investment.
On a subject basis, which annuity do you think is more attractive
and why?
Find the future value at the end of year 6,for both annuity x and Y.

43. 43
NUMERICALS
what is the present value of $ 6000 to be received at the end
of 6 years if the discount rate is 12%?
$100 at the end of three years is worth how much today,
assuming a discount rate of
100%
10%
0%

44. 44
Example of an
Annuity Due -- FVAD
Cash flows occur at the beginning of the period
0
1
2
3
$1,000
$1,000
4
$1,070
7%
$1,000
$1,145
$1,225
FVAD3 = $1,000(1.07)3 +
$1,000(1.07)2 + $1,000(1.07)1
= $1,225 + $1,145 + $1,070
= $3,440
$3,440 = FVAD3

45. 45
Valuation Using Table III
FVADn
FVAD3
= R (FVIFAi%,n)(1+i)
= $1,000 (FVIFA7%,3)(1.07)
= $1,000 (3.215)(1.07) = $3,440
Period
6%
7%
8%
1
1.000
1.000
1.000
2
2.060
2.070
2.080
3
3.184
3.215
3.246
4
4.375
4.440
4.506
5
5.637
5.751
5.867

46. 46
Present value of ordinary
annuity
PVA=PMT(PVIFAi,n)
PVIF=
1 - 1
(1+i)n
i

47. 47
PRESENT VALUE OF
ANNUITY DUE
PVIF=PVIFA*(1+i)

48. 48
PV of an ordinary annuity
Braden company a small producer of toys wants to determine the
most it should pay to purchase a particular ordinary annuity. the
annuity consist of cash flows of 700v at the end of each year for 5
years. The firm requires the annuity to provide a minimum return
of 8%.

49. 49
Long method for finding the
present value of an ordinary
annuity
Year
CF
PVIF8%,n
(1)
(2)
1
700
0.926
2
700
0.857
3
700
0.794
4
700
0.735
5
700
0.681
present value of annuity=2795.10
PVIF=1/i*(1-1/(1+i)n)
PV
(1*2)
648.20
599.90
555.80
514.50
476.70

50. 50
Finding present value of an
Ordinary Annuity -- PVA
Cash flows occur at the end of the period
0
1
2
n
n+1
. . .
i%
R
R
R
R = Periodic
Cash Flow
PVAn
PVAn = R/(1+i)1 + R/(1+i)2
+ ... + R/(1+i)n

51. 51
Example of an
Ordinary Annuity -- PVA
Cash flows occur at the end of the period
0
1
2
3
$1,000
$1,000
$1,000
7%
$ 934.58
$ 873.44
$ 816.30
$2,624.32 = PVA3
PVA3 =
$1,000/(1.07)1 +
$1,000/(1.07)2 +
$1,000/(1.07)3
= $934.58 + $873.44 + $816.30
= $2,624.32
4

52. 52
Hint on Annuity Valuation
The present value of an ordinary
annuity can be viewed as
occurring at the beginning of the
first cash flow period, whereas
the present value of an annuity
due can be viewed as occurring
at the end of the first cash flow
period.

53. 53
Valuation Using Table IV
PVAn
PVA3
= R (PVIFAi%,n)
= $1,000 (PVIFA7%,3)
= $1,000 (2.624) = $2,624
Period
6%
7%
8%
1
0.943
0.935
0.926
2
1.833
1.808
1.783
3
2.673
2.624
2.577
4
3.465
3.387
3.312
5
4.212
4.100
3.993

54. 54
Overview of an
Annuity Due -- PVAD
Cash flows occur at the beginning of the period
0
1
2
PVADn
n
. . .
i%
R
n-1
R
R
R
R: Periodic
Cash Flow
PVADn = R/(1+i)0 + R/(1+i)1 + ... + R/(1+i)n-1
= PVAn (1+i)

55. 55
Example of an
Annuity Due -- PVAD
Cash flows occur at the beginning of the period
0
1
2
$1,000
3
$1,000
7%
$1,000.00
$ 934.58
$ 873.44
$2,808.02 = PVADn
PVADn = $1,000/(1.07)0 + $1,000/(1.07)1 +
$1,000/(1.07)2 = $2,808.02
4

56. 56
Valuation Using Table IV
PVADn = R (PVIFAi%,n)(1+i)
PVAD3 = $1,000 (PVIFA7%,3)(1.07)
= $1,000 (2.624)(1.07) = $2,808
Period
6%
7%
8%
1
0.943
0.935
0.926
2
1.833
1.808
1.783
3
2.673
2.624
2.577
4
3.465
3.387
3.312
5
4.212
4.100
3.993

57. 57
Steps to Solve Time Value
of Money Problems
1. Read problem thoroughly
2. Determine if it is a PV or FV problem
3. Create a time line
4. Put cash flows and arrows on time line
5. Determine if solution involves a single
CF, annuity stream(s), or mixed flow
6. Solve the problem
7. Check with financial calculator (optional)

58. 58
Mixed Flows Example
Julie Miller will receive the set of cash
flows below. What is the Present Value
at a discount rate of 10%?
10%
0
1
10%
$600
PV0
2
3
4
5
$600 $400 $400 $100

59. 59
How to Solve?
1. Solve a “piece-at-a-time” by
piece-at-a-time
discounting each piece back to t=0.
2. Solve a “group-at-a-time” by first
group-at-a-time
breaking problem into groups
of annuity streams and any single
cash flow group. Then discount
each group back to t=0.

60. 60
“Piece-At-A-Time”
0
1
10%
$600
2
3
4
5
$600 $400 $400 $100
$545.45
$495.87
$300.53
$273.21
$ 62.09
$1677.15 = PV0 of the Mixed Flow

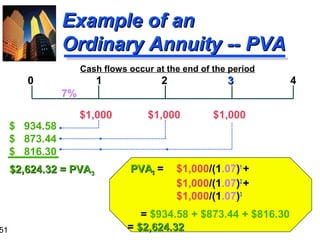
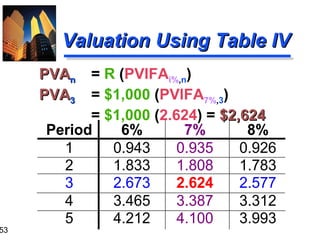
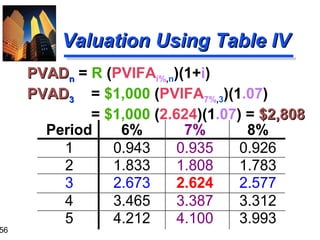
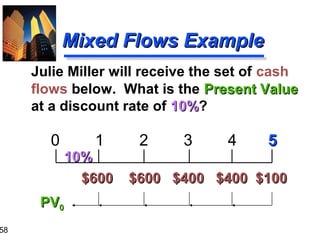
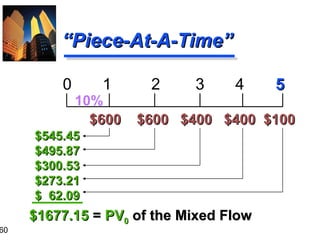
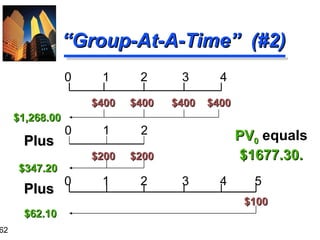
61. 61
“Group-At-A-Time” (#1)
0
10%
1
$600
2
3
4
5
$600 $400 $400 $100
$1,041.60
$ 573.57
$ 62.10
$1,677.27 = PV0 of Mixed Flow [Using Tables]
$600(PVIFA10%,2) =
$600(1.736) = $1,041.60
$400(PVIFA10%,2)(PVIF10%,2) = $400(1.736)(0.826) = $573.57
$100 (PVIF10%,5) =
$100 (0.621) =
$62.10

62. 62
“Group-At-A-Time” (#2)
0
Plus
$347.20
Plus
$62.10
0
3
$400
$400
1
2
$200
0
2
$400
$1,268.00
1
$200
1
2
4
$400
PV0 equals
$1677.30.
3
4
5
$100

63. 63
Frequency of
Compounding
General Formula:
FVn = PV0(1 + [i/m])mn
n:
Number of Years
m:
Compounding Periods per Year
i:
Annual Interest Rate
FVn,m: FV at the end of Year n
PV0:
PV of the Cash Flow today

64. 64
Impact of Frequency
Julie Miller has $1,000 to invest for 2
years at an annual interest rate of
12%.
Annual
FV2
= 1,000(1+ [.12/1])(1)(2)
1,000
= 1,254.40
Semi
FV2
= 1,000(1+ [.12/2])(2)(2)
1,000
= 1,262.48

65. 65
Impact of Frequency
Qrtly
FV2
= 1,000(1+ [.12/4])(4)(2)
1,000
= 1,266.77
Monthly
FV2
= 1,000(1+ [.12/12])(12)(2)
1,000
= 1,269.73
Daily
FV2
= 1,000(1+[.12/365])(365)(2)
1,000
= 1,271.20

66. 66
Present value of perpetuity
An annuity with an infinite life,
providing continual annual cash
flow
PVIF=1/i

67. 67
Effective Annual
Interest Rate
The annual rate of interest actually
paid or earned
The actual rate of interest earned
(paid) after adjusting the nominal
rate for factors such as the number
of compounding periods per year.
(1 + [ i / m ] )m - 1

68. 68
Nominal annual rate
Contractual annual rate of
interest charged by a lender or
promised by a borrower.

69. 69
BW’s Effective
Annual Interest Rate
Basket Wonders (BW) has a $1,000
CD at the bank. The interest rate
is 6% compounded quarterly for 1
year. What is the Effective Annual
Interest Rate (EAR)?
EAR
EAR = ( 1 + 6% / 4 )4 - 1
= 1.0614 - 1 = .0614 or 6.14%!

70. 70
Loan amortization
The determination of the equal
periodic loan payments
necessary to provide lender with
a specified interest return and to
repay the loan principal over a
specified period.

71. 71
Steps to Amortizing a Loan
1.
Calculate the payment per period.
2.
Determine the interest in Period t.
(Loan balance at t-1) x (i% / m)
3.
Compute principal payment in Period t.
(Payment - interest from Step 2)
4.
Determine ending balance in Period t.
(Balance - principal payment from Step 3)
5.
Start again at Step 2 and repeat.

72. 72
Amortizing a Loan Example
Julie Miller is borrowing $22,000 at a
compound annual interest rate of 12%.
Amortize the loan if annual payments are
made for 5 years.
Step 1: Payment
PV0 = R (PVIFA i%,n)
$22,000
= R (PVIFA 12%,5)
$22,000
= R (3.605)
R = $22,000 / 3.605 = $5351

73. 73
Amortizing a Loan Example
End of Payment
Year
0
---
Interest Principal Ending
(Pmt-int) Balance
----$22,000
1
$5351
2640
2711
19289
2
5351
2315
3036
16253
3
5351
1951
3400
12853
4
5351
1542
3809
9044
5
5351
1085
4266
4778
6
5351
573
4778
0

74. 74
Usefulness of Amortization
1.
2.
Determine Interest Expense -Interest expenses may reduce
taxable income of the firm.
Calculate Debt Outstanding -- The
quantity of outstanding debt
may be used in financing the
day-to-day activities of the firm.