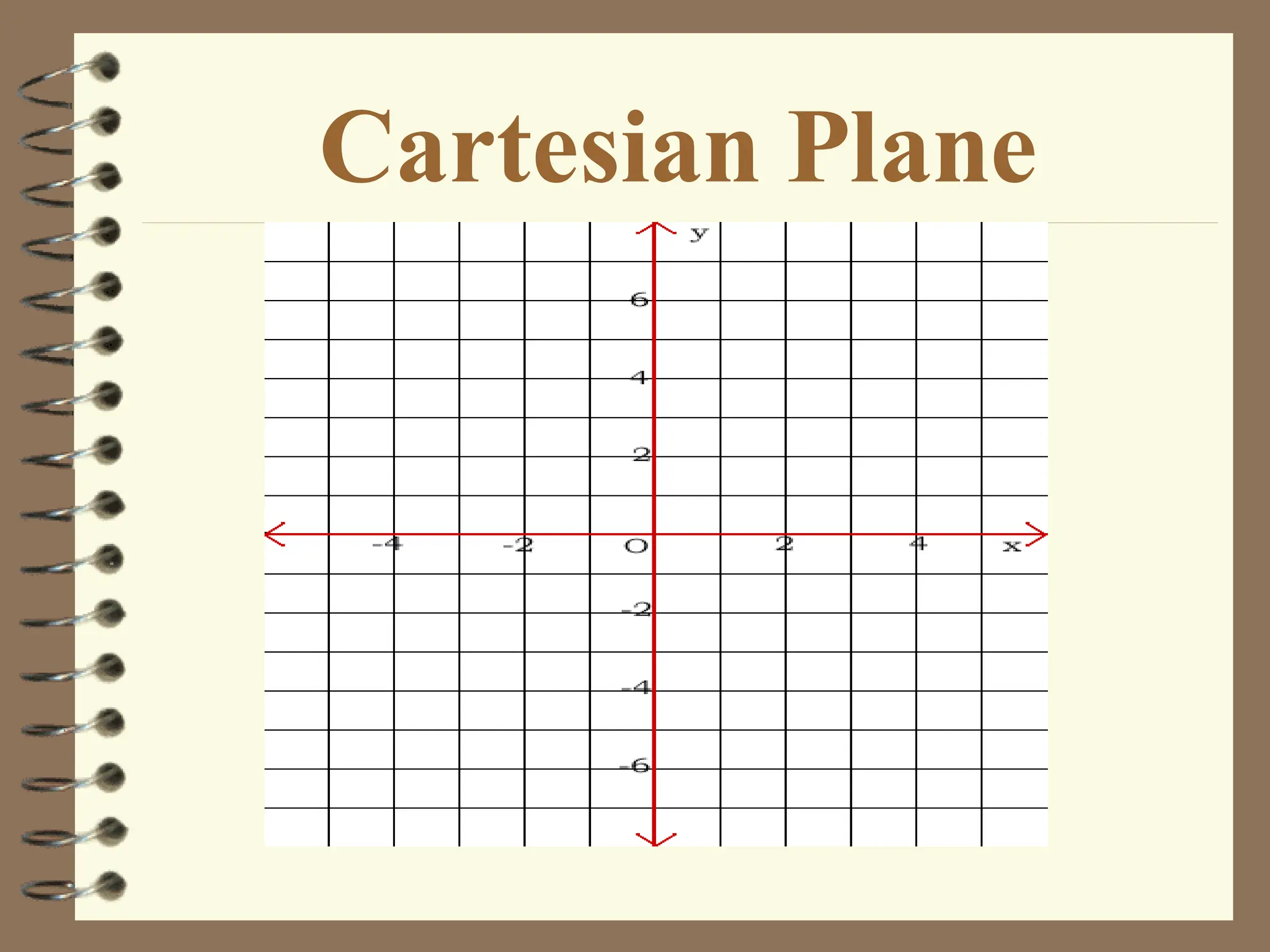
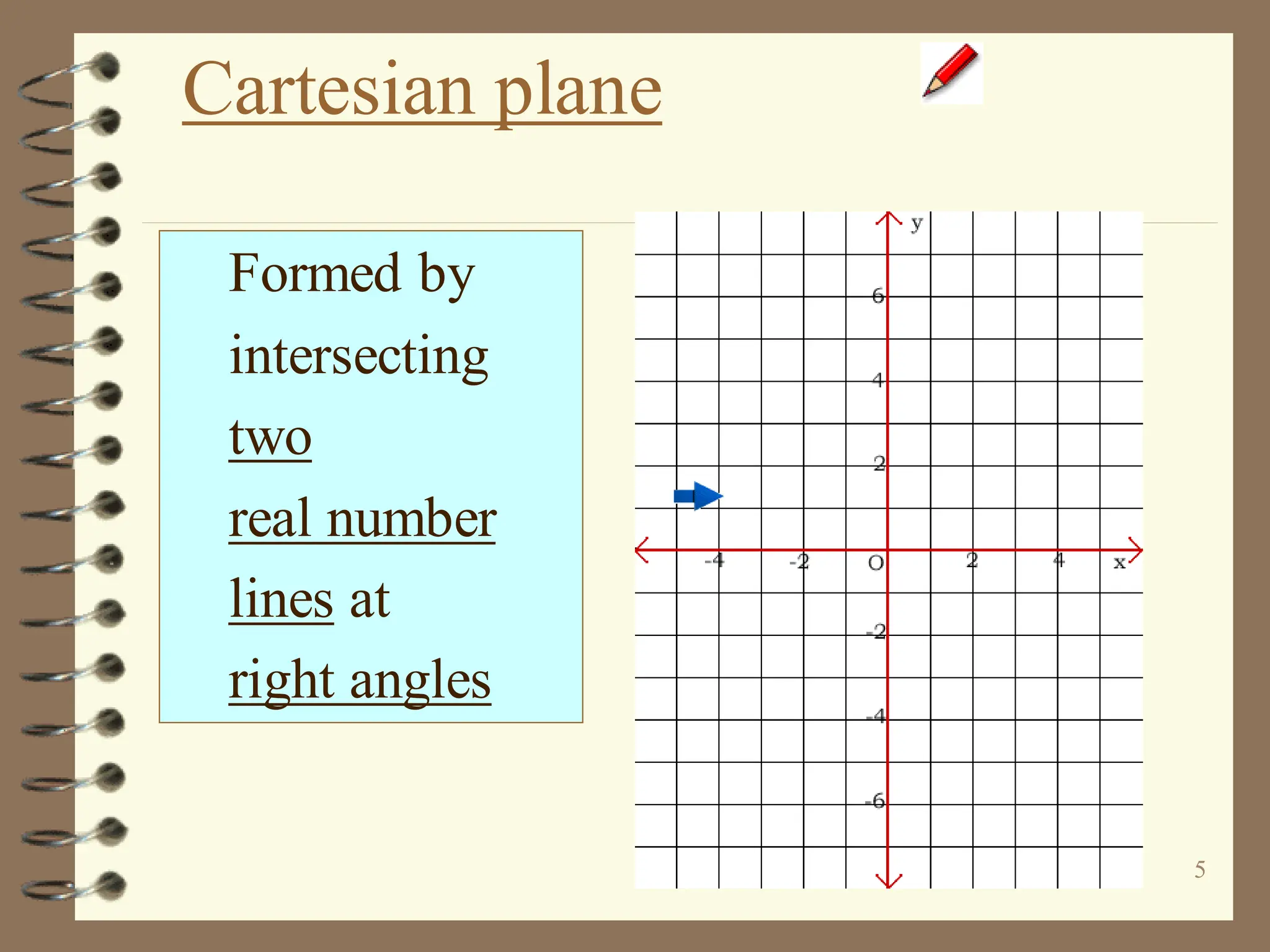
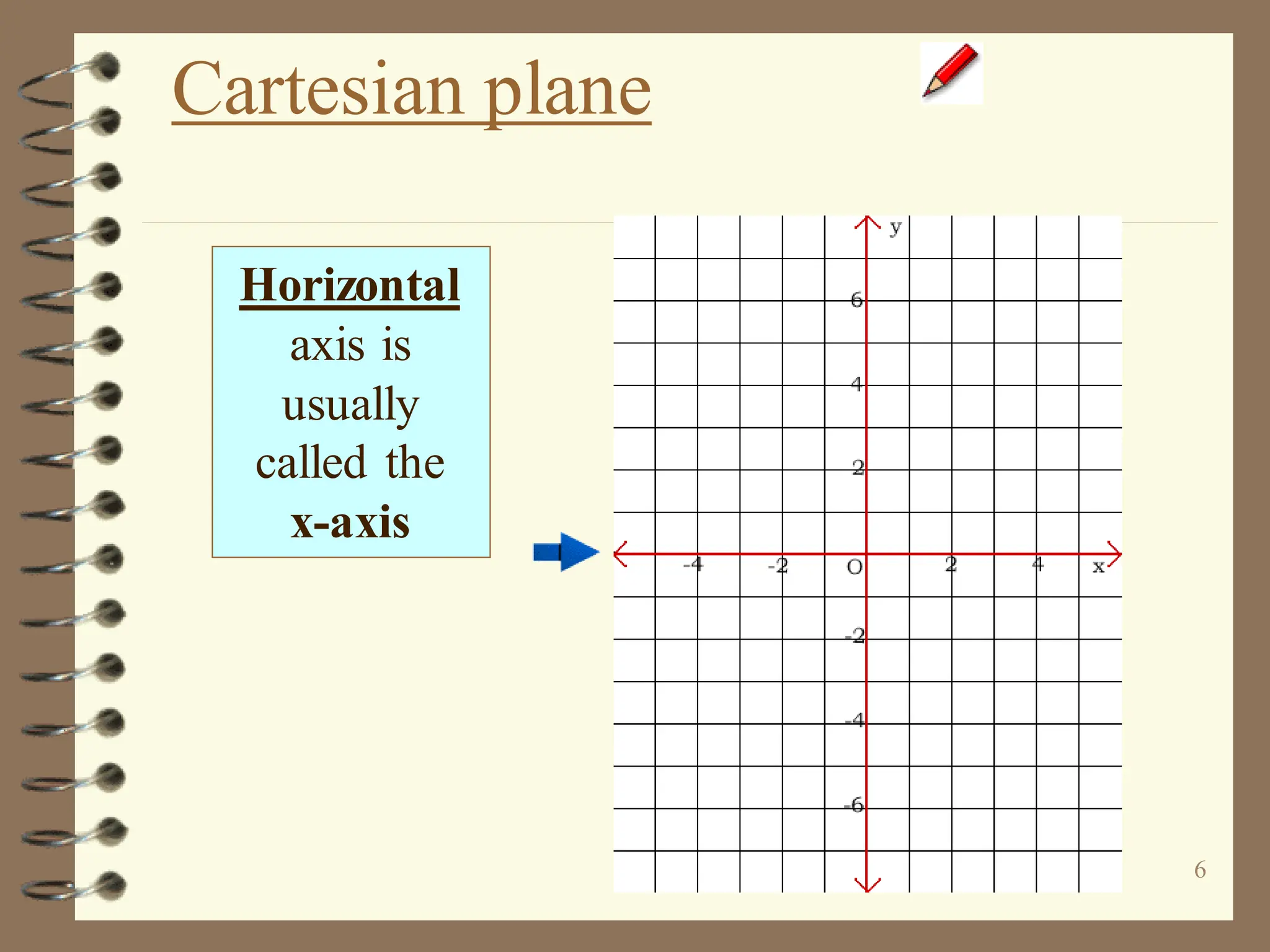
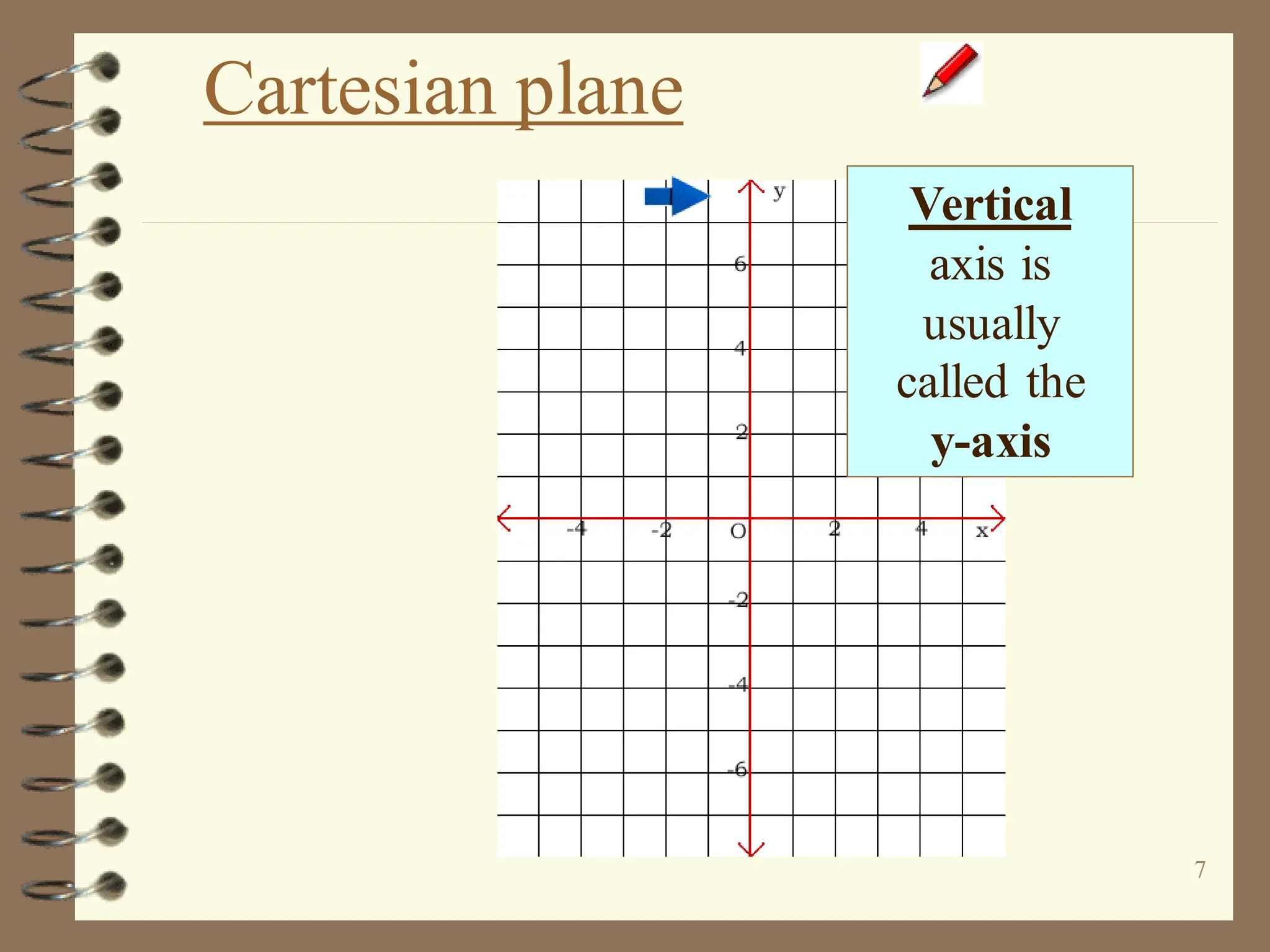
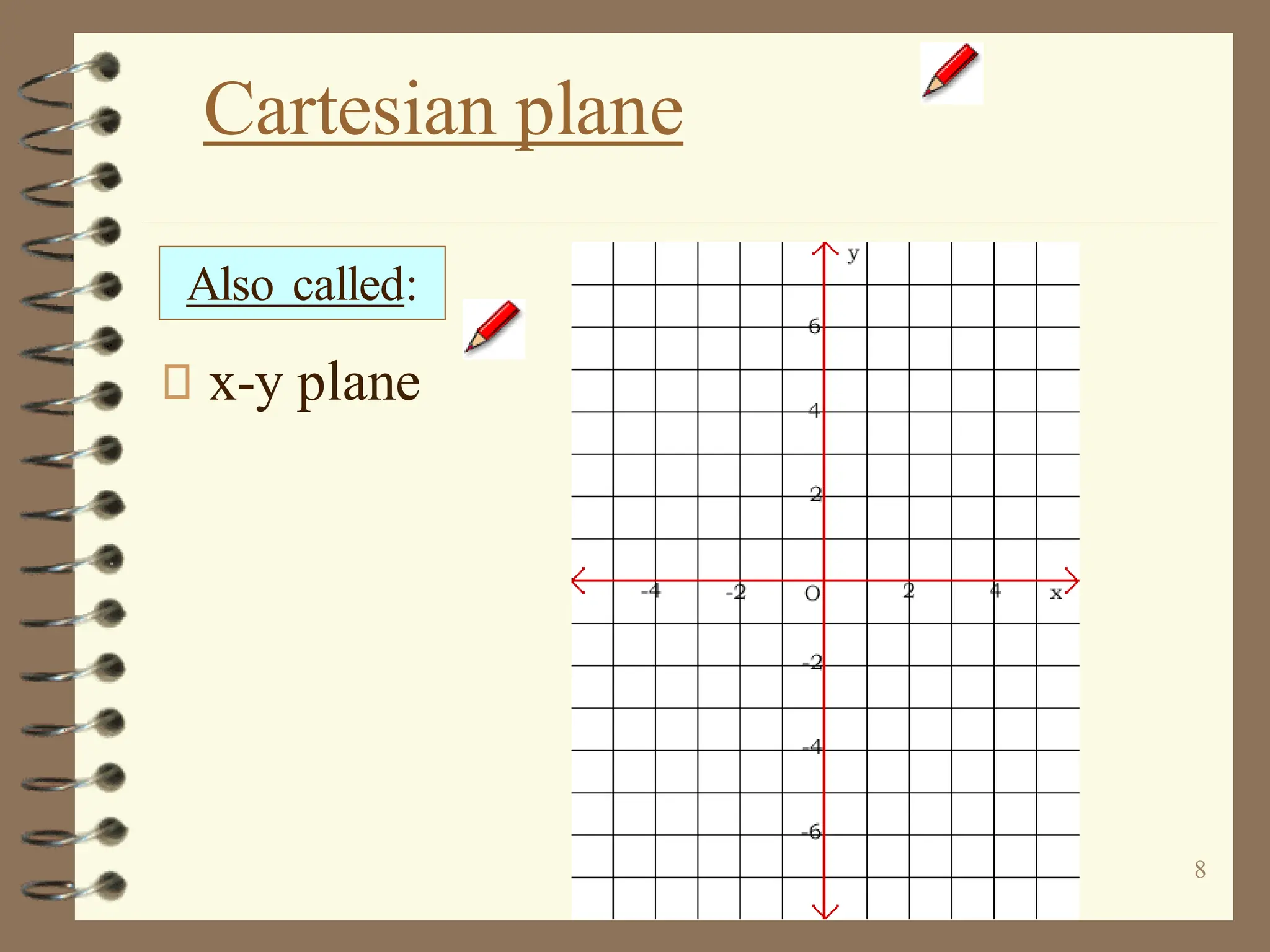
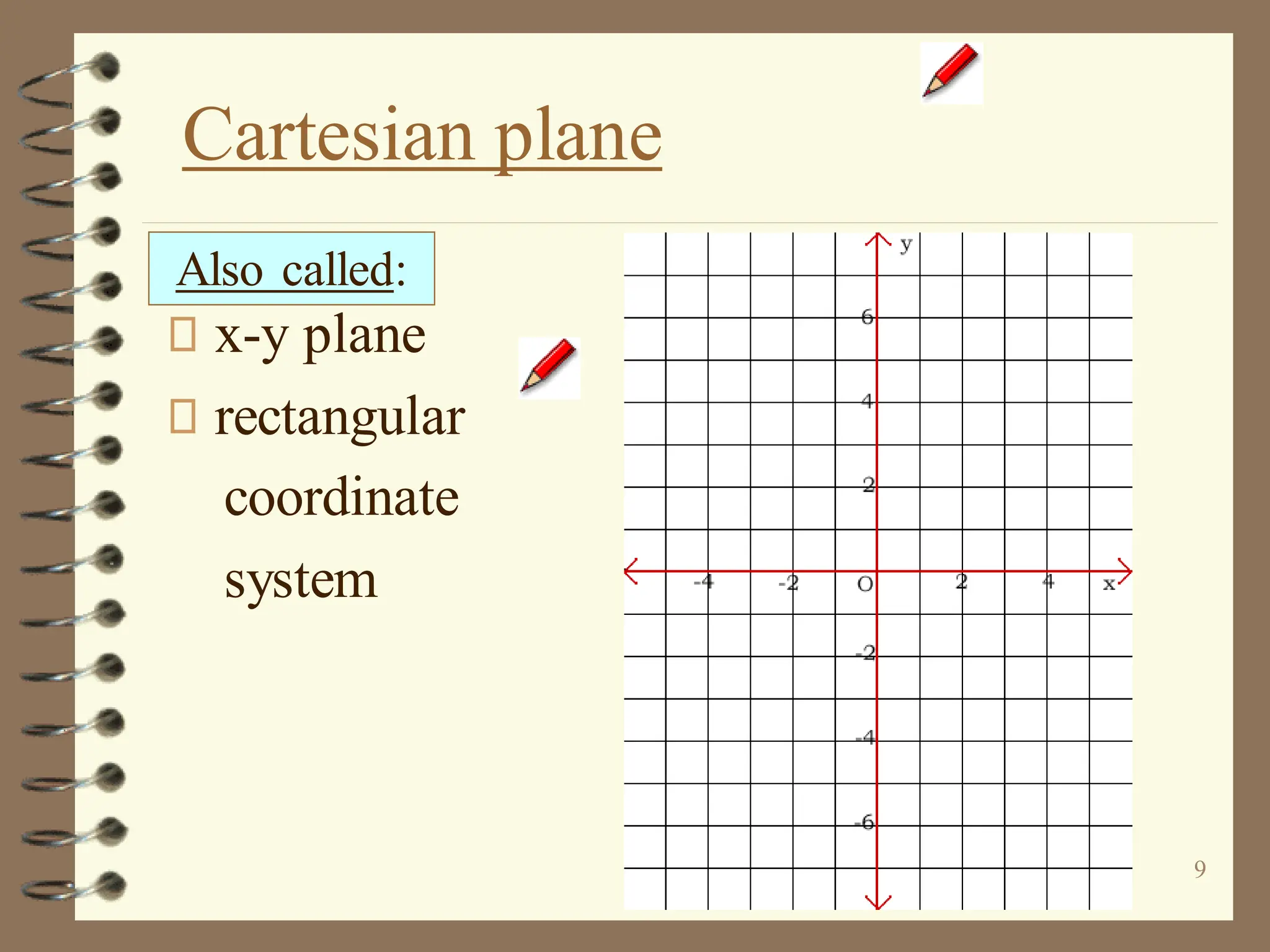
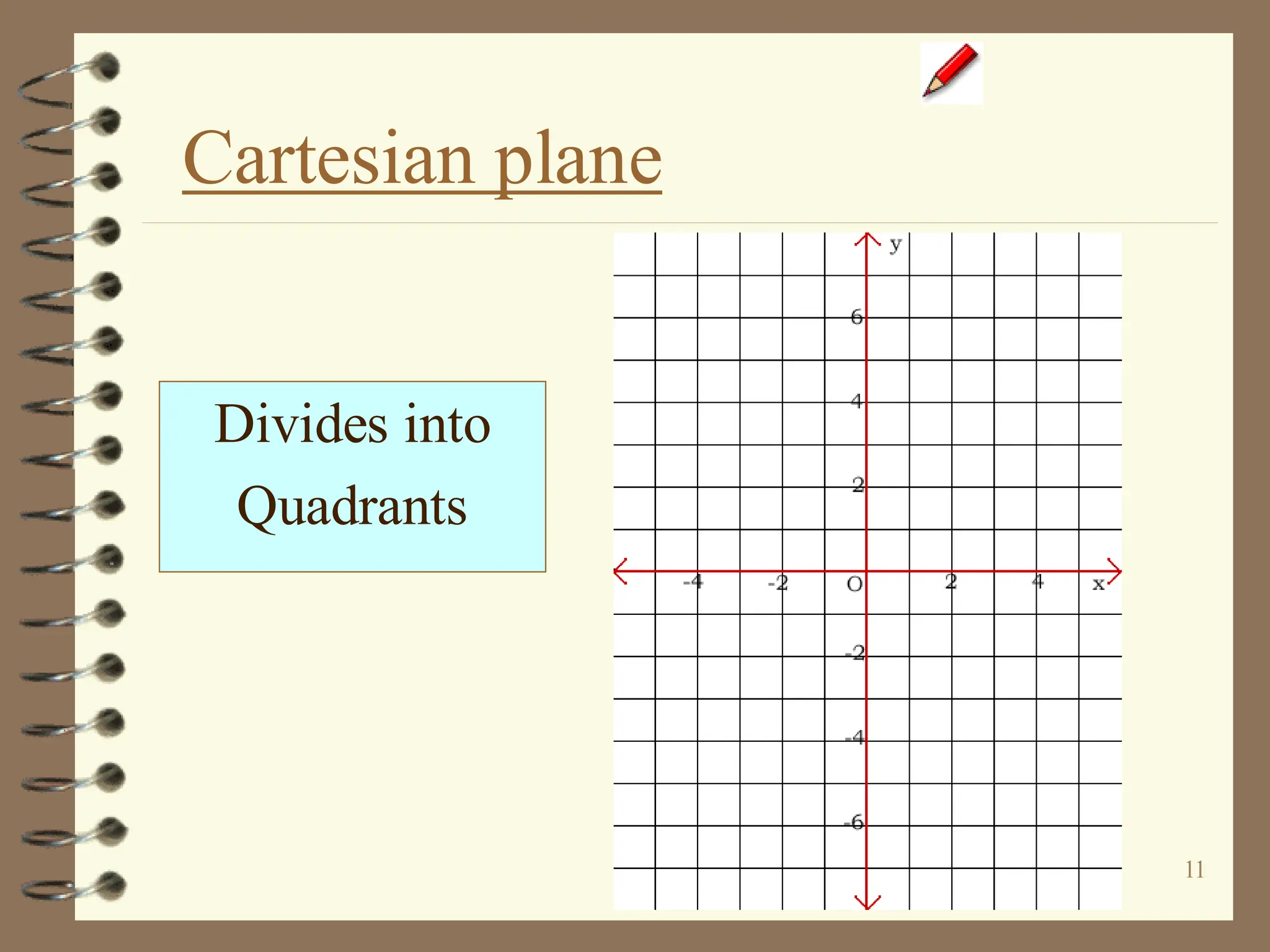
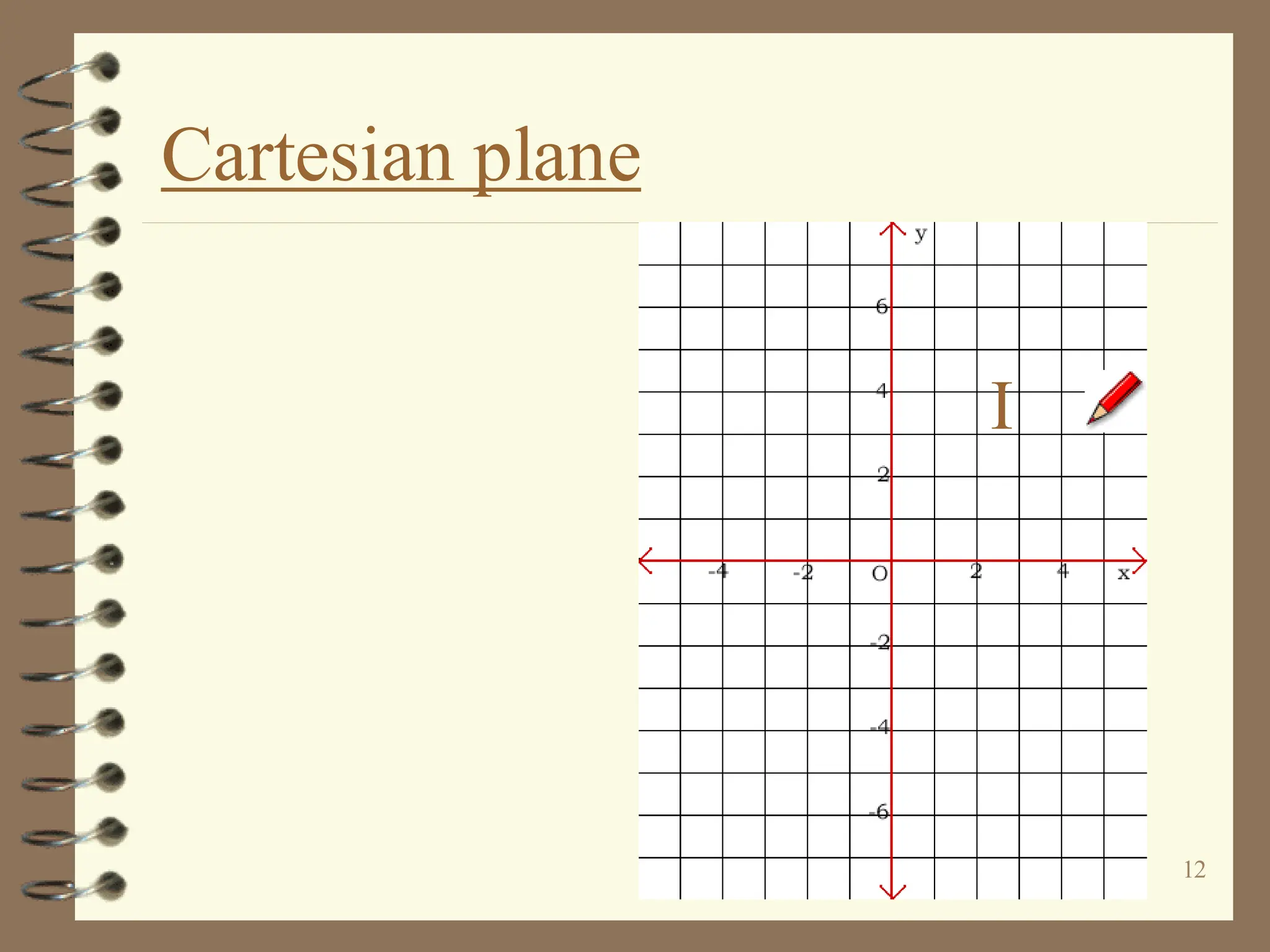
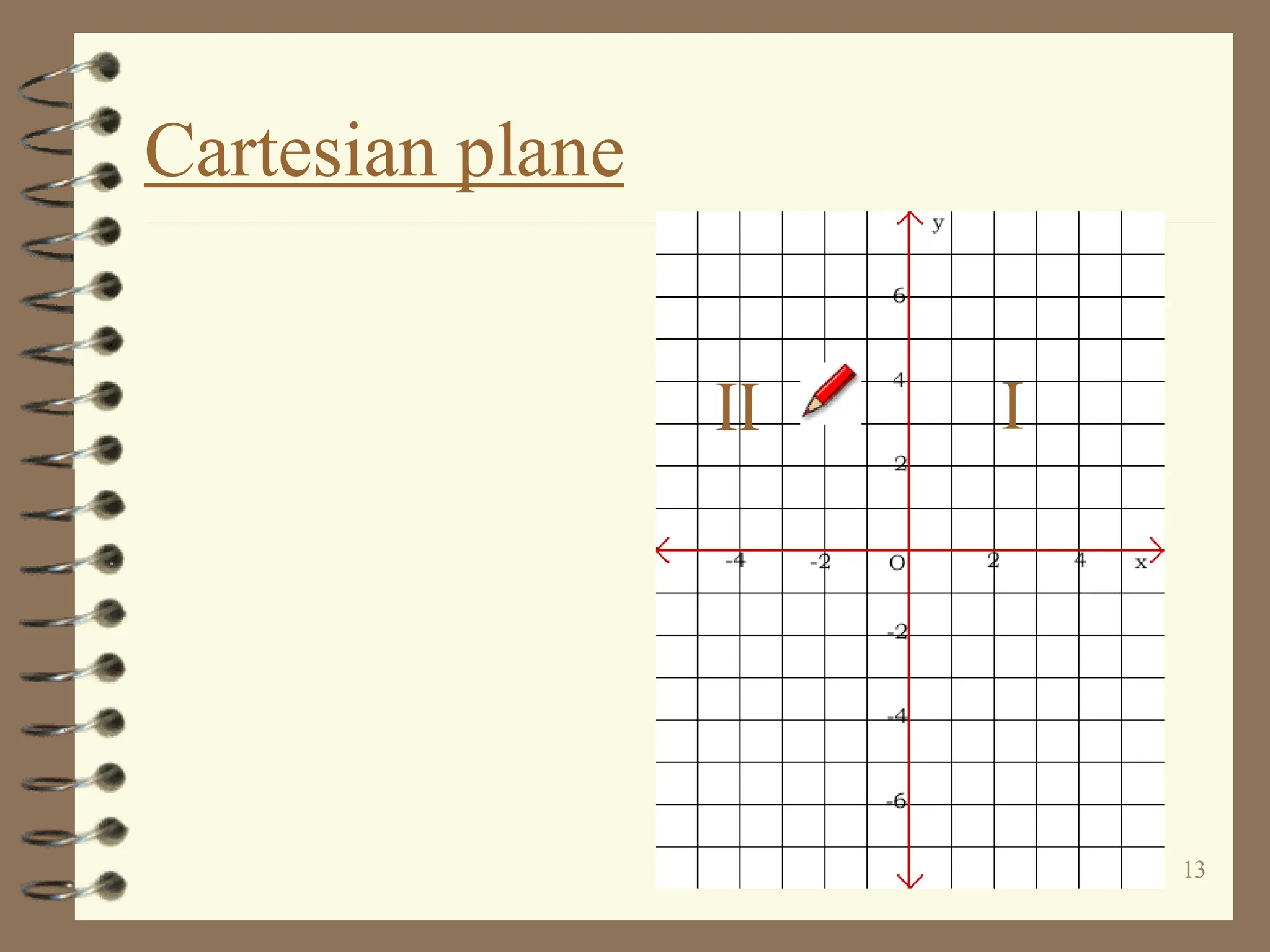
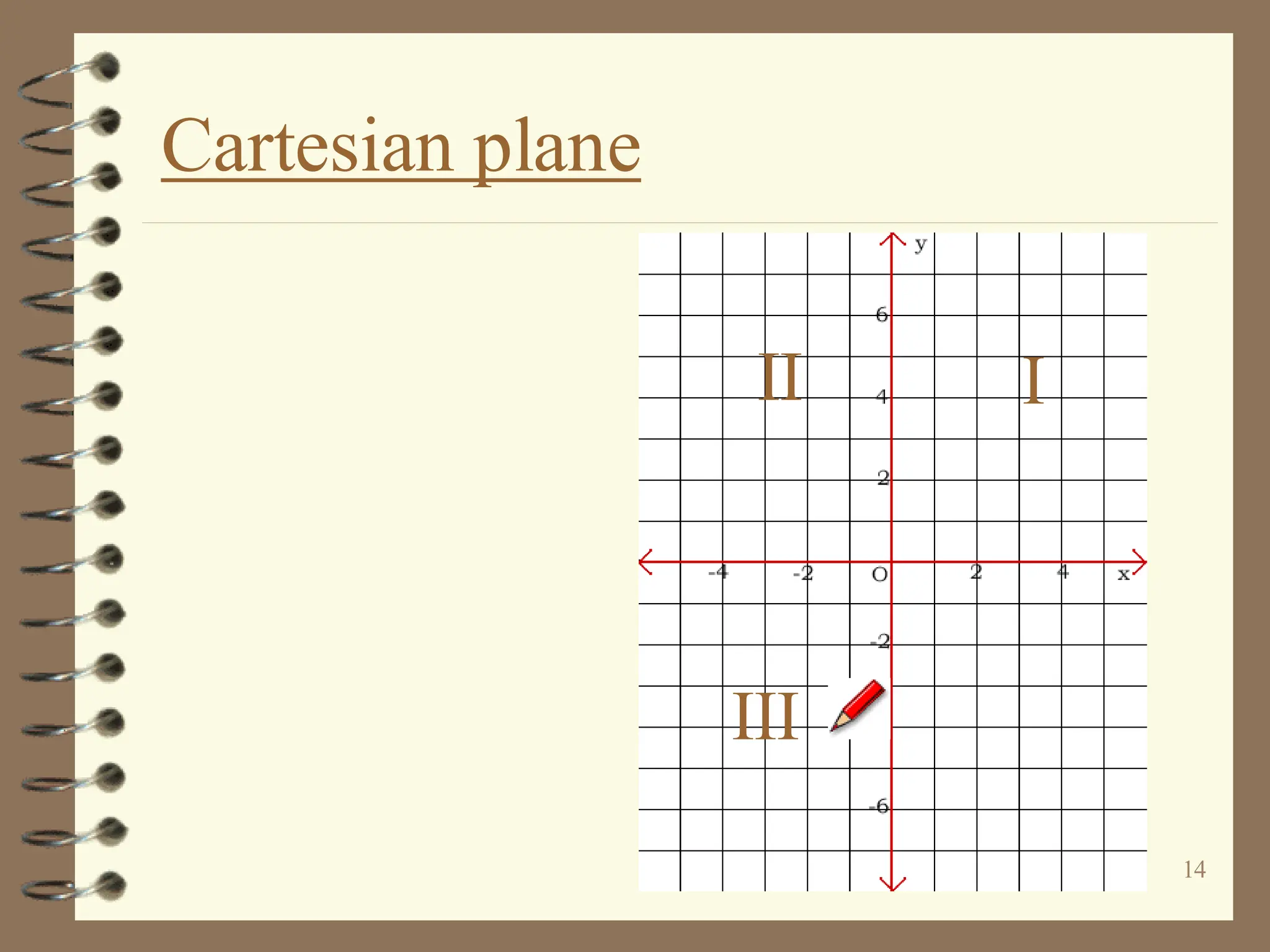
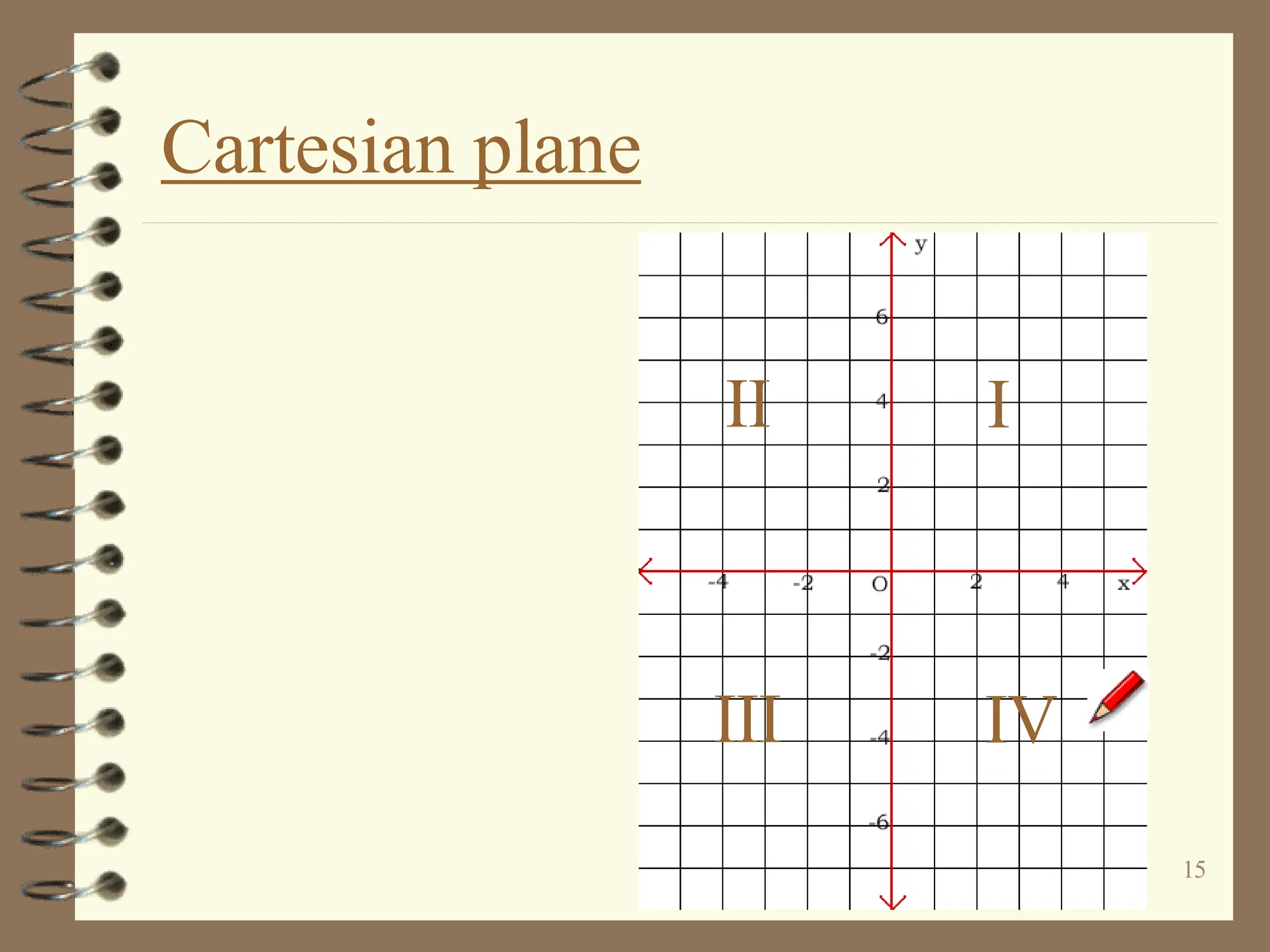
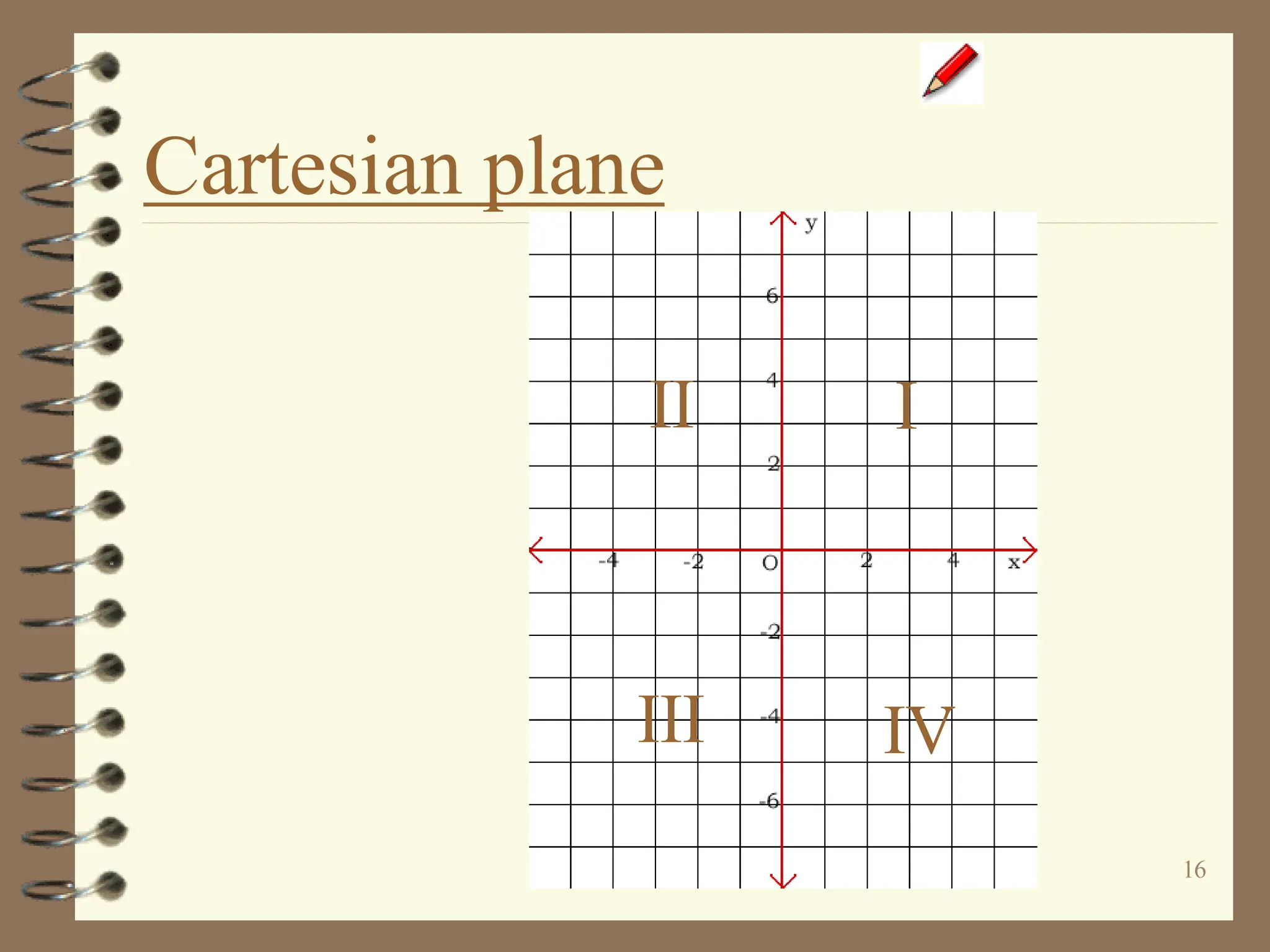
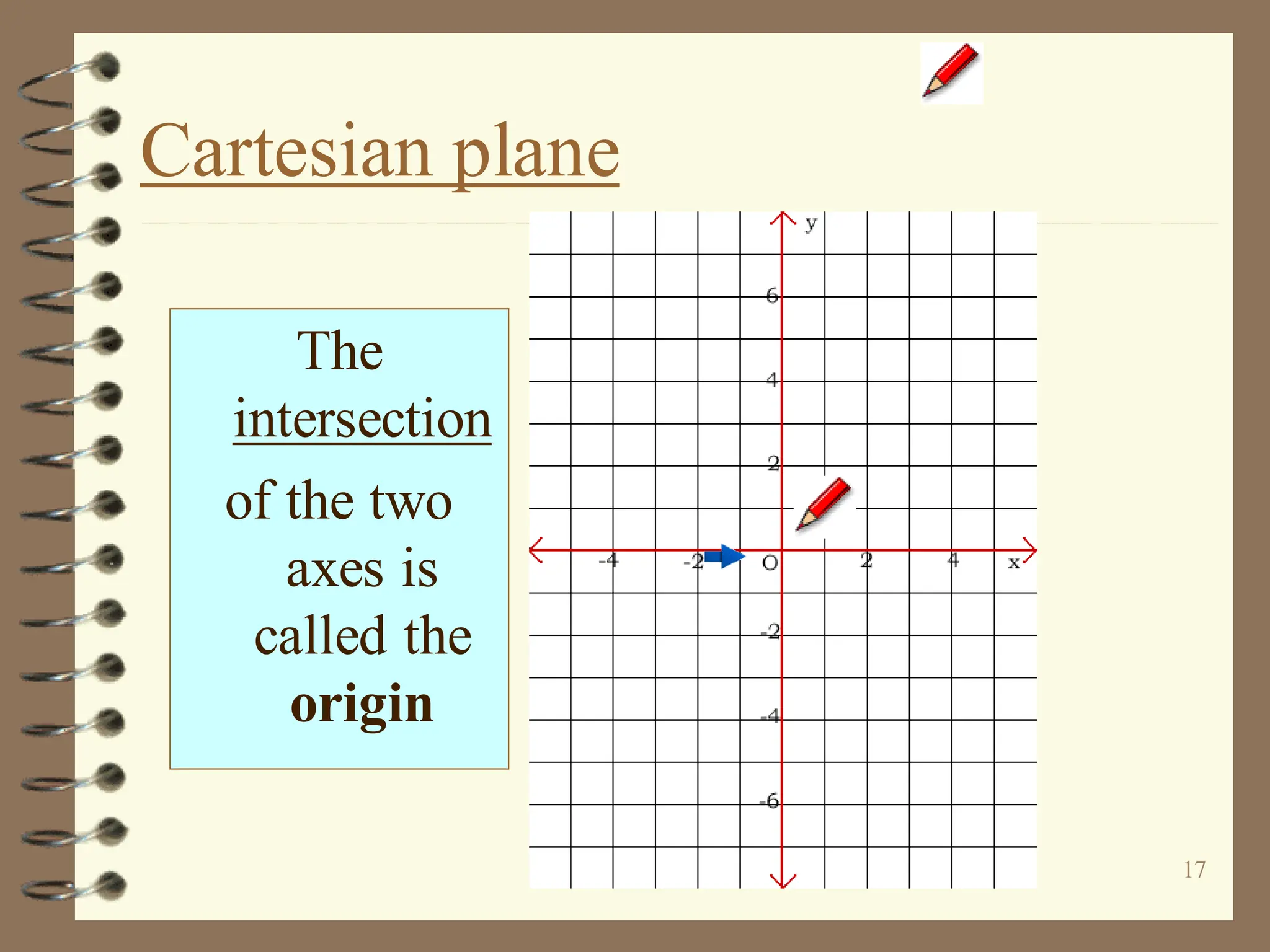
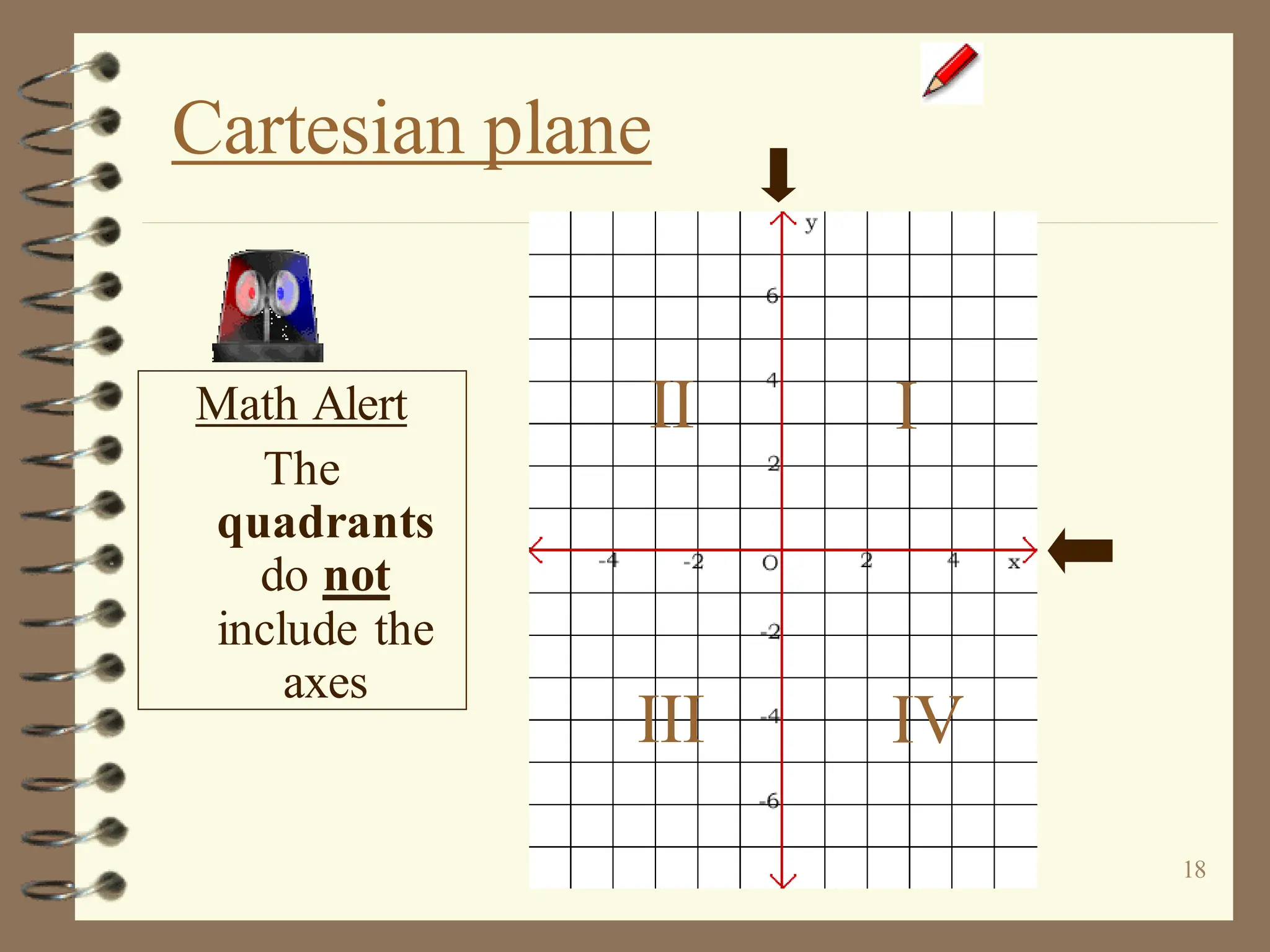
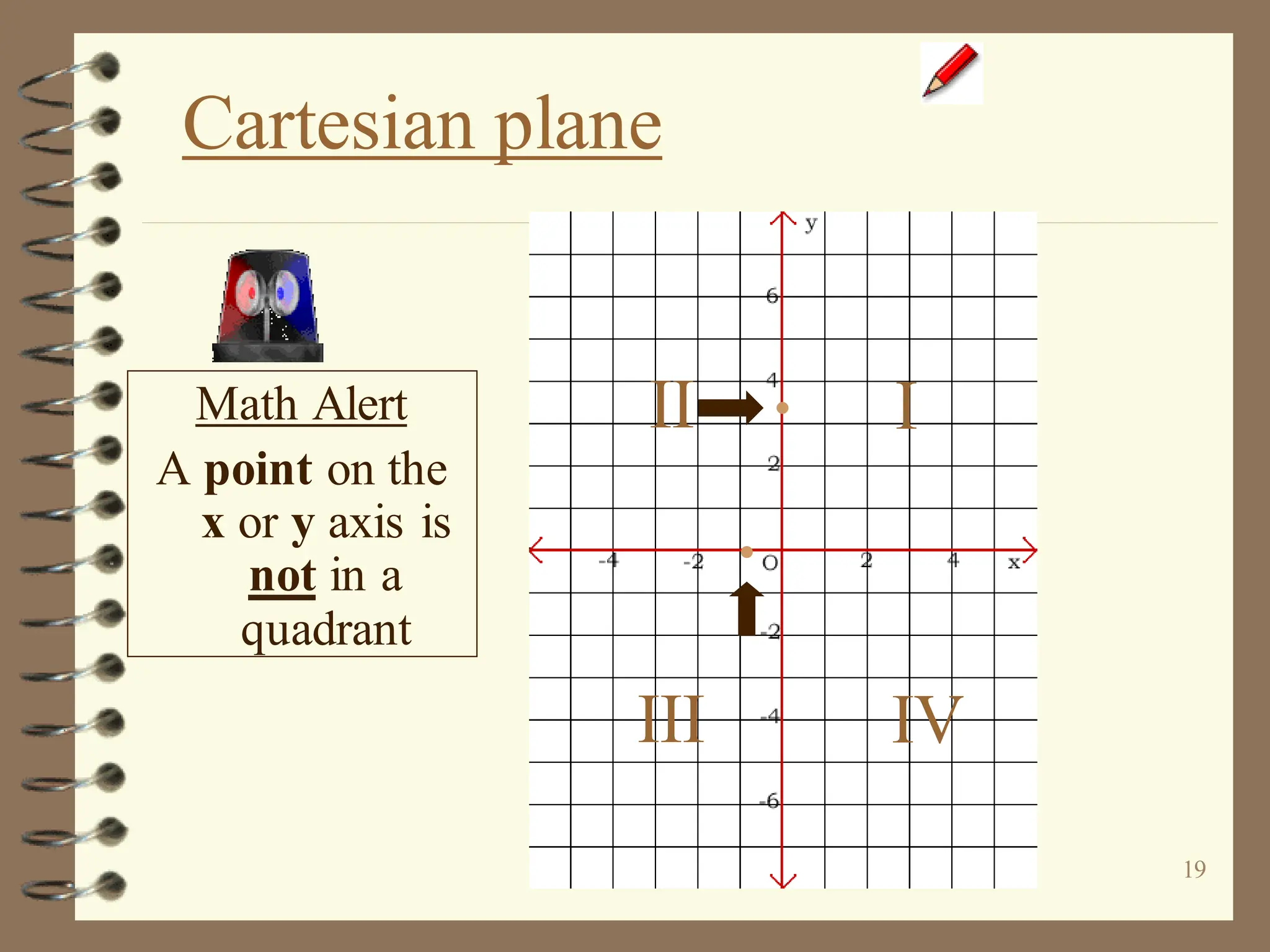
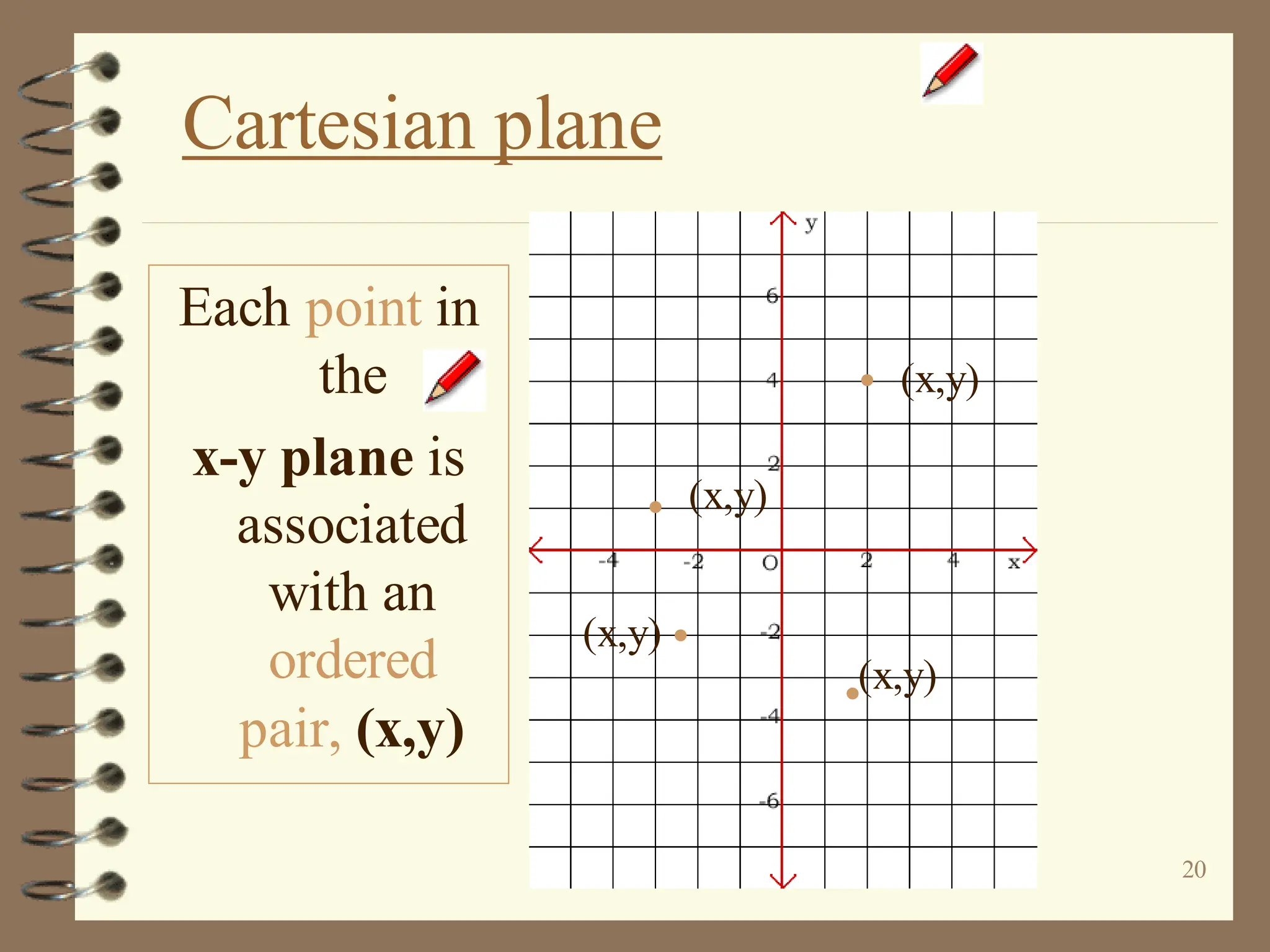
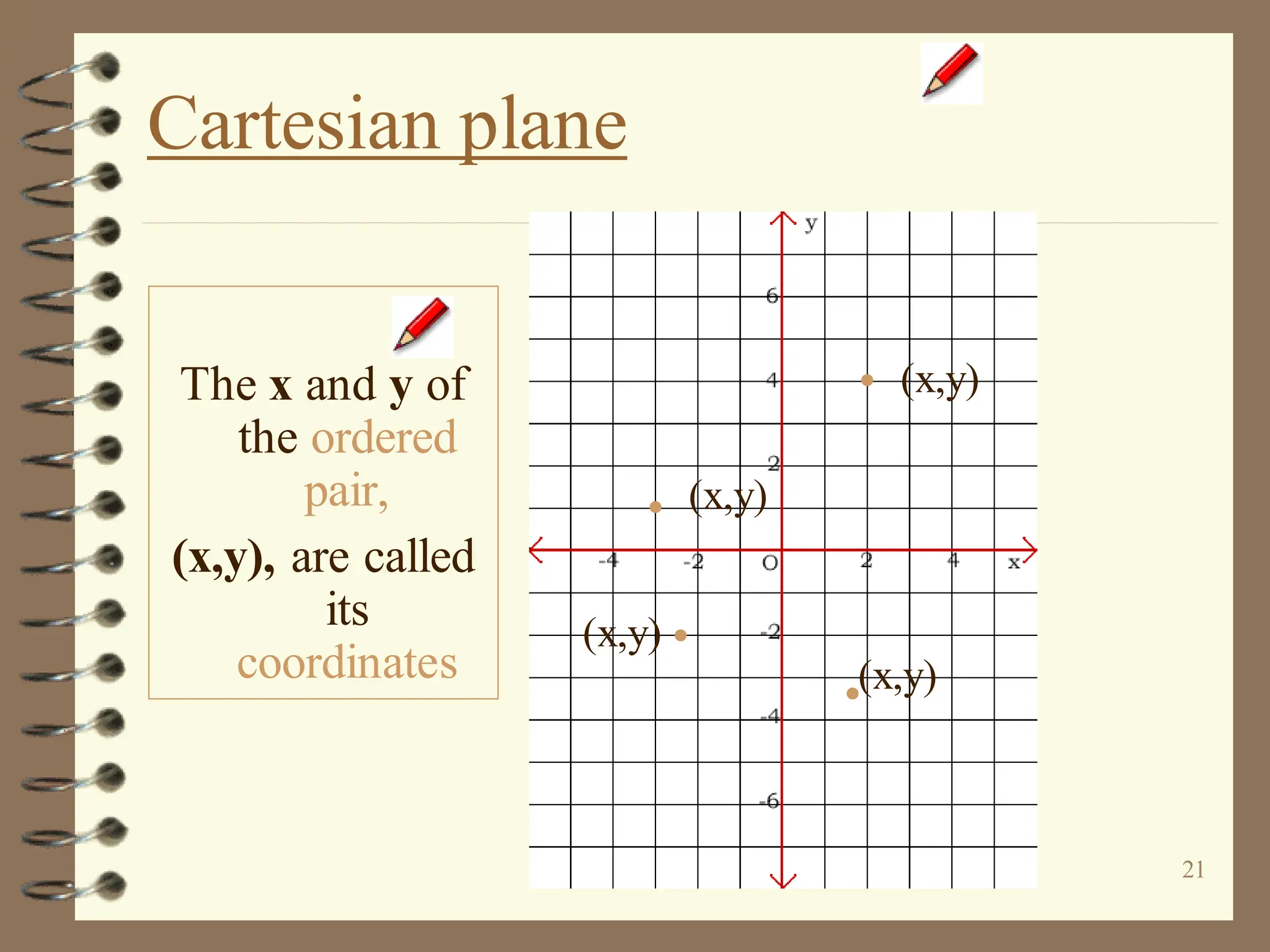
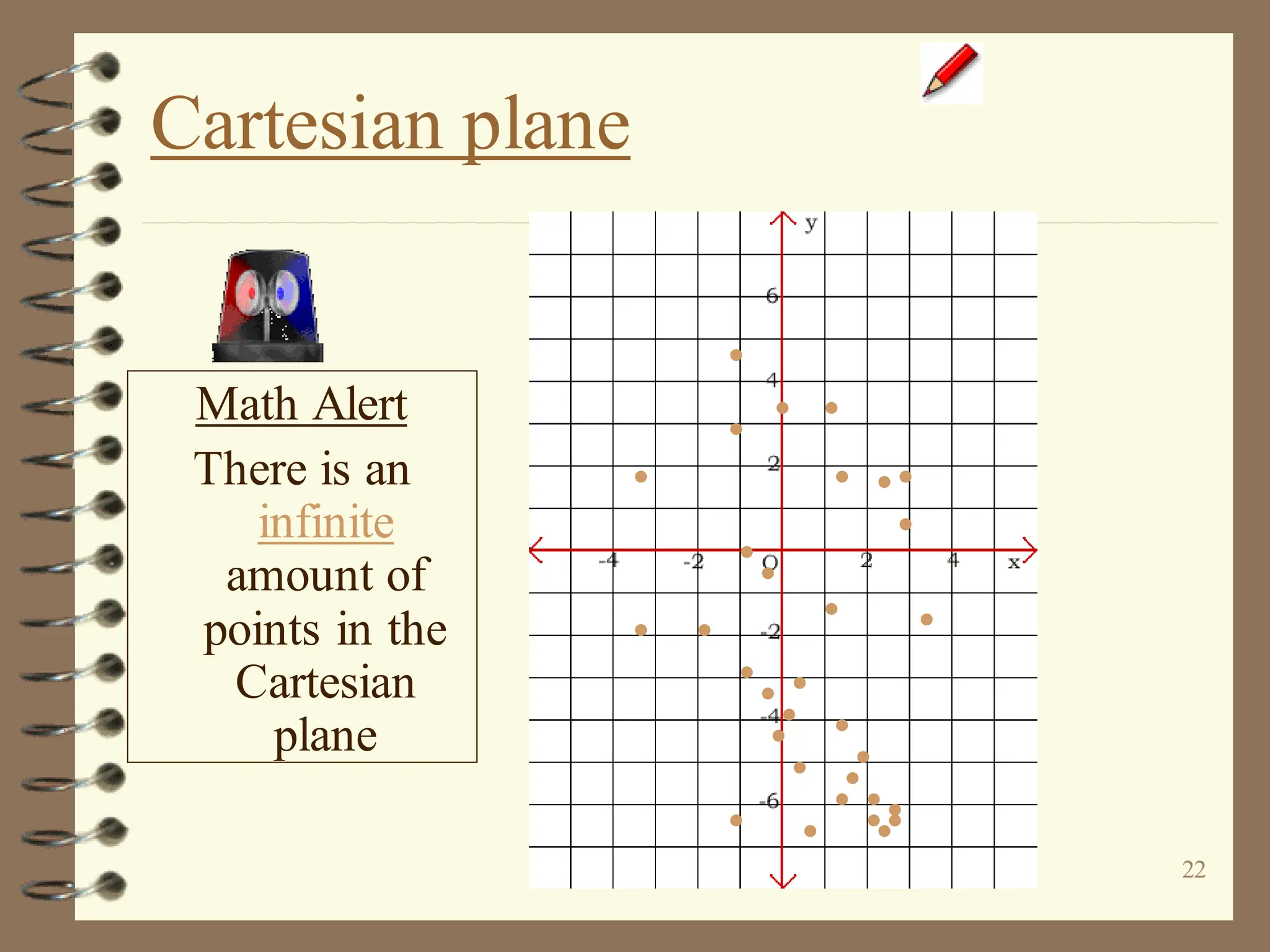
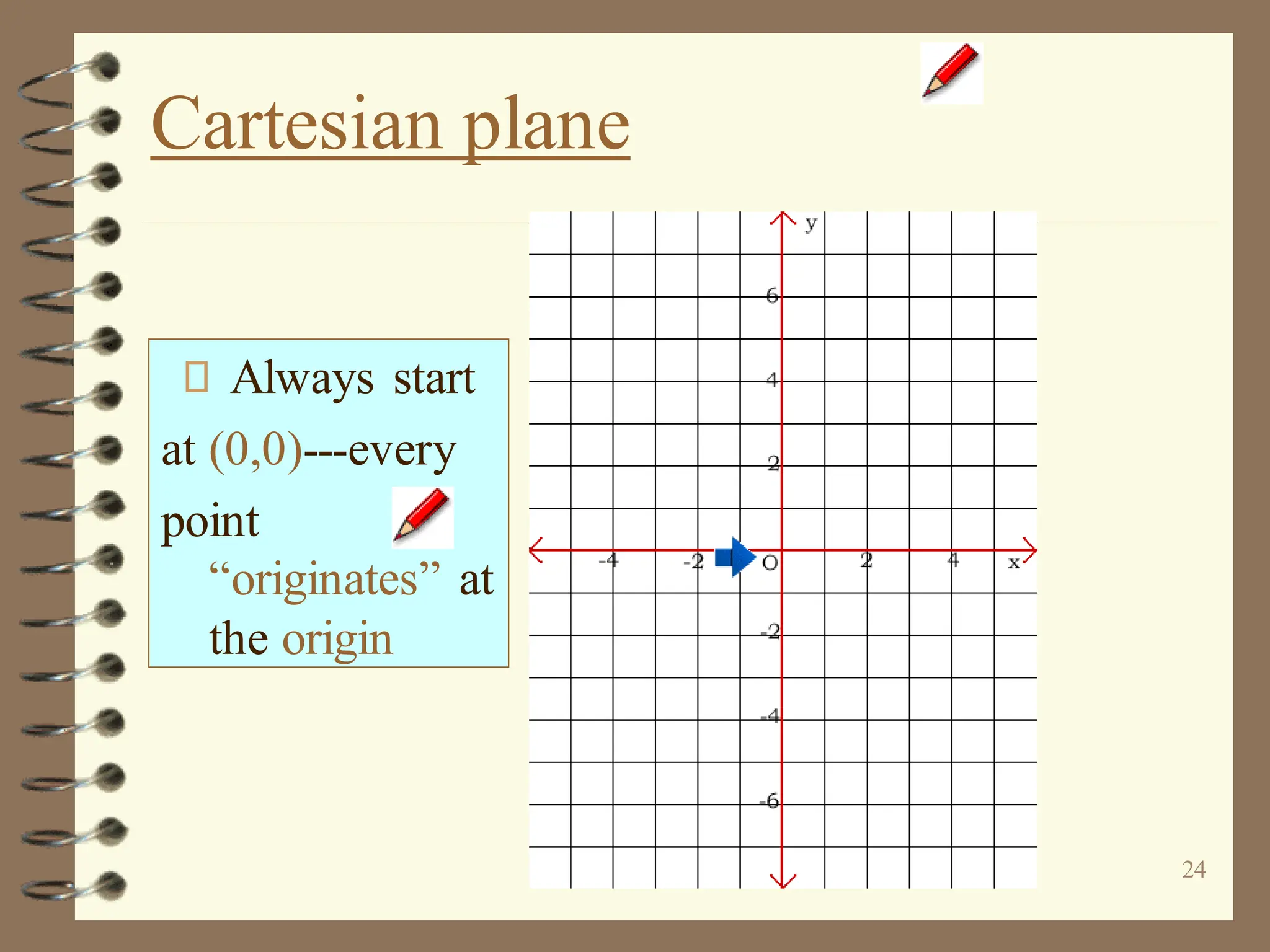
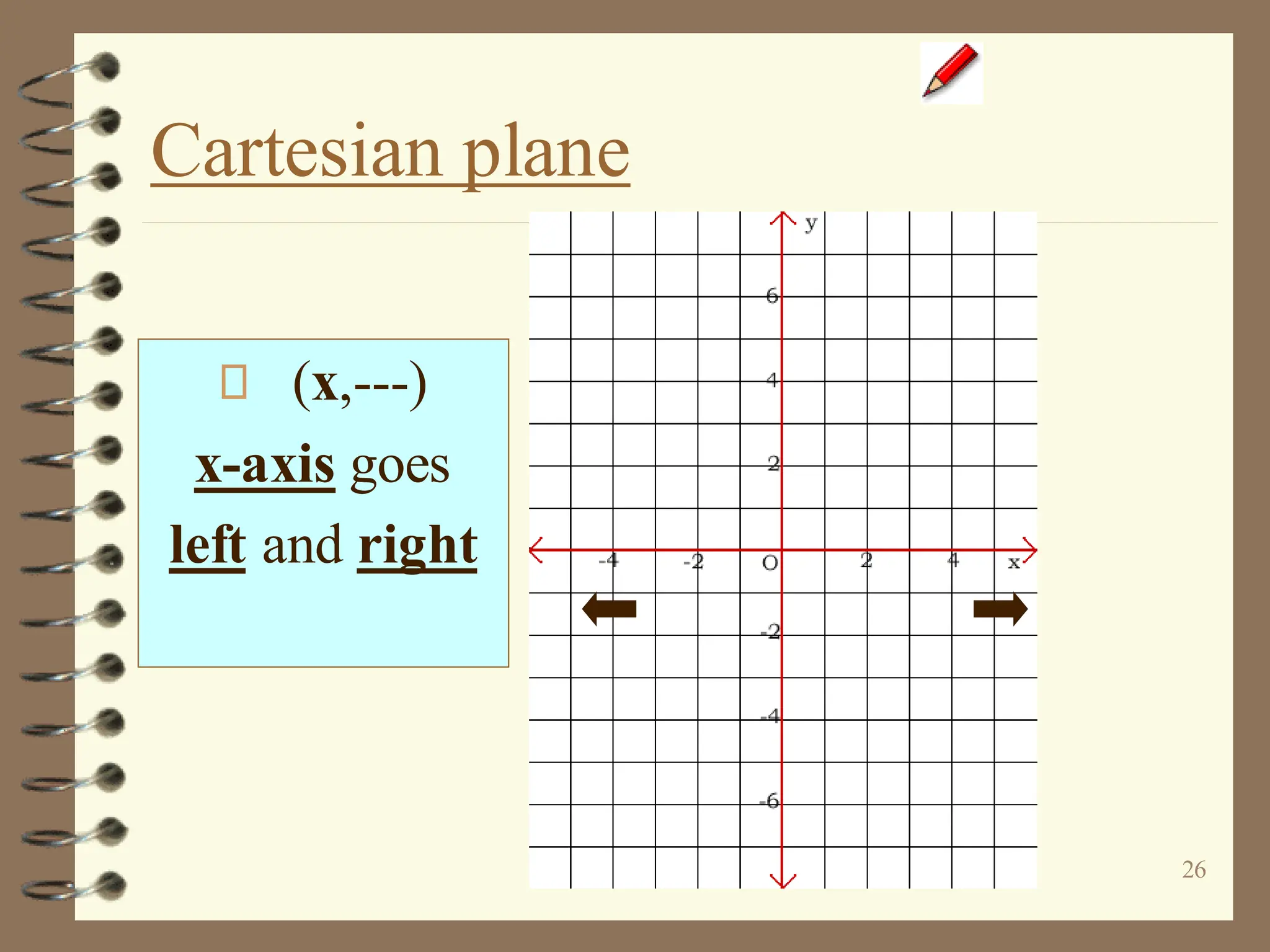
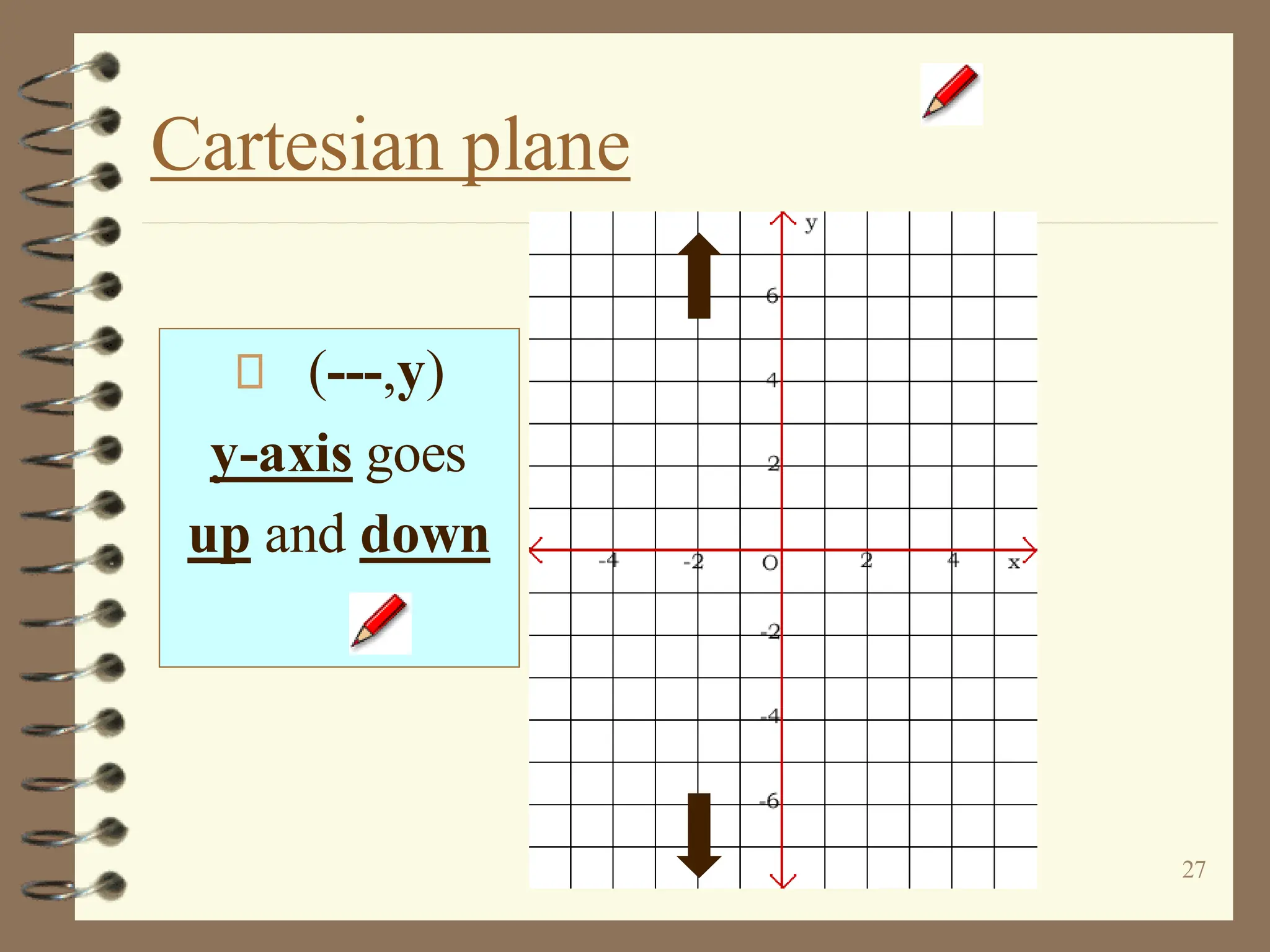
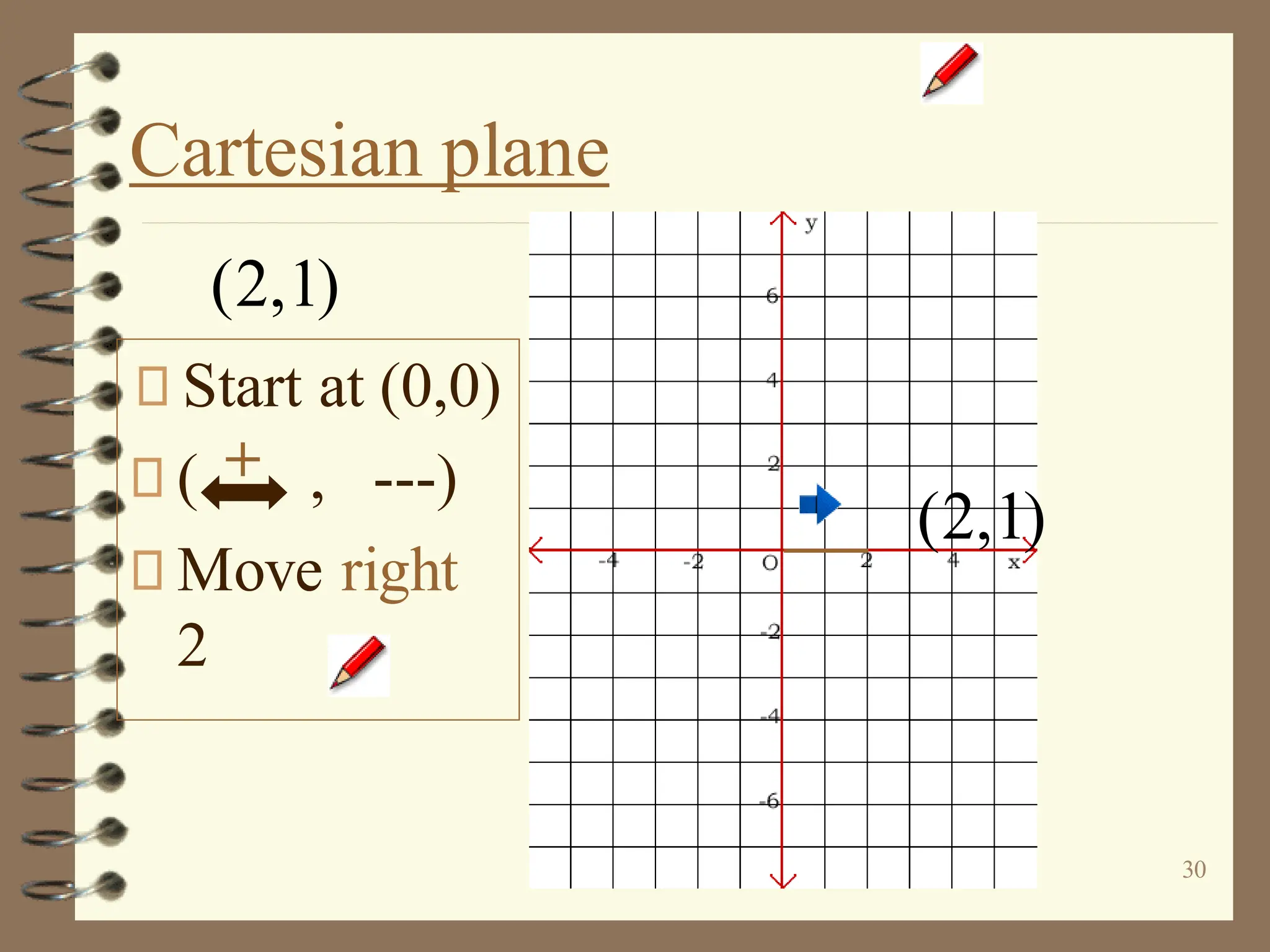
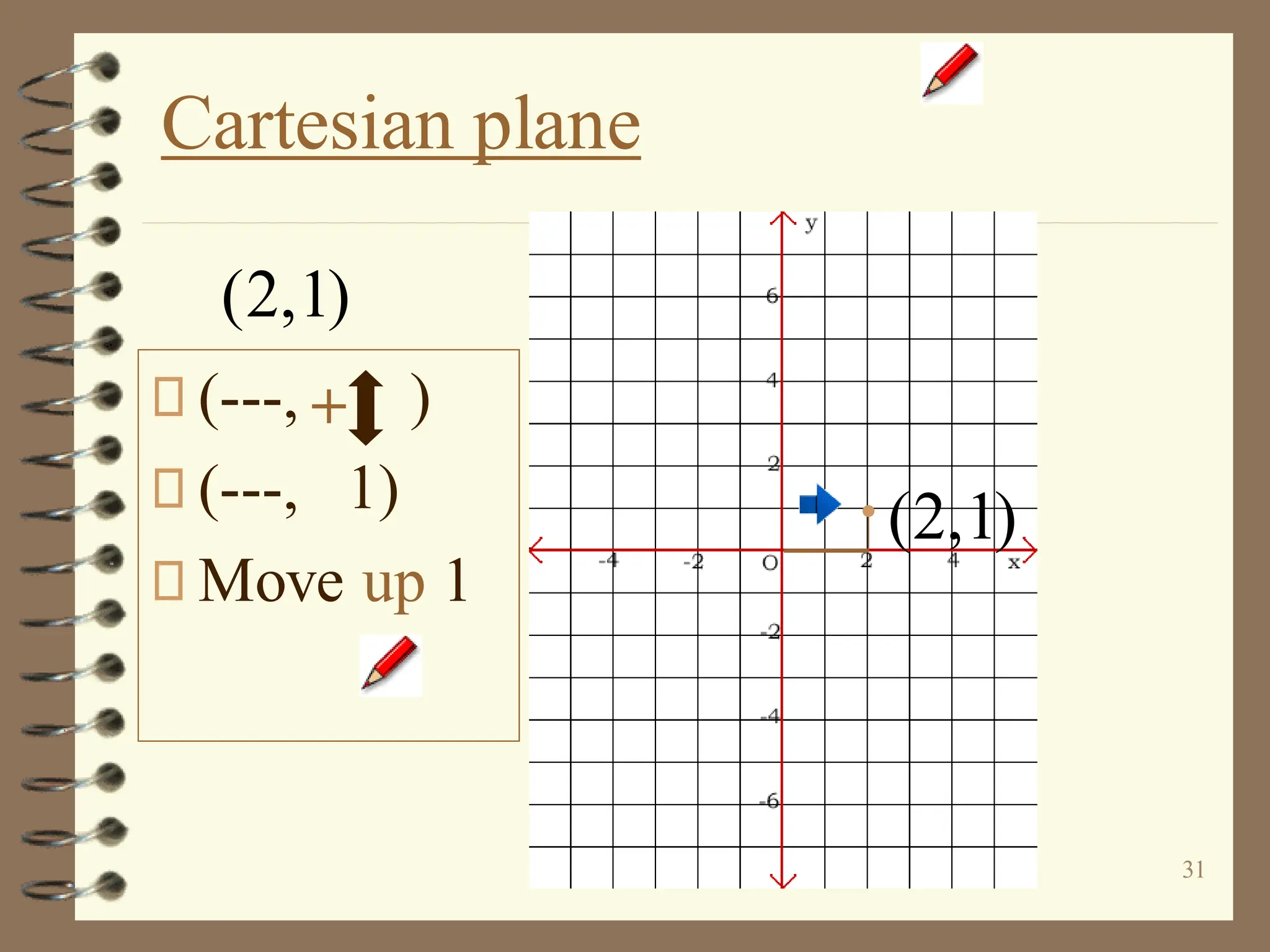
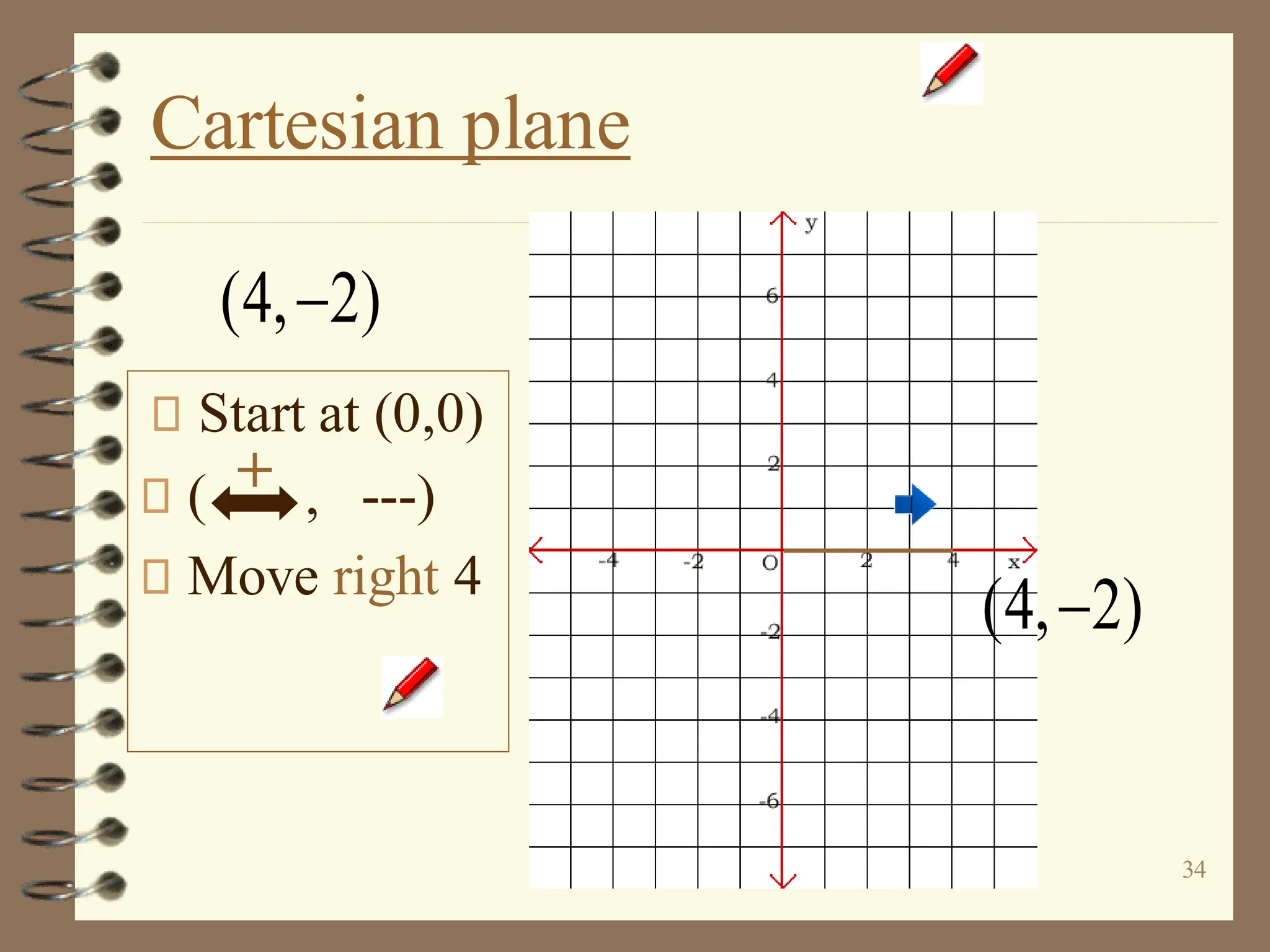
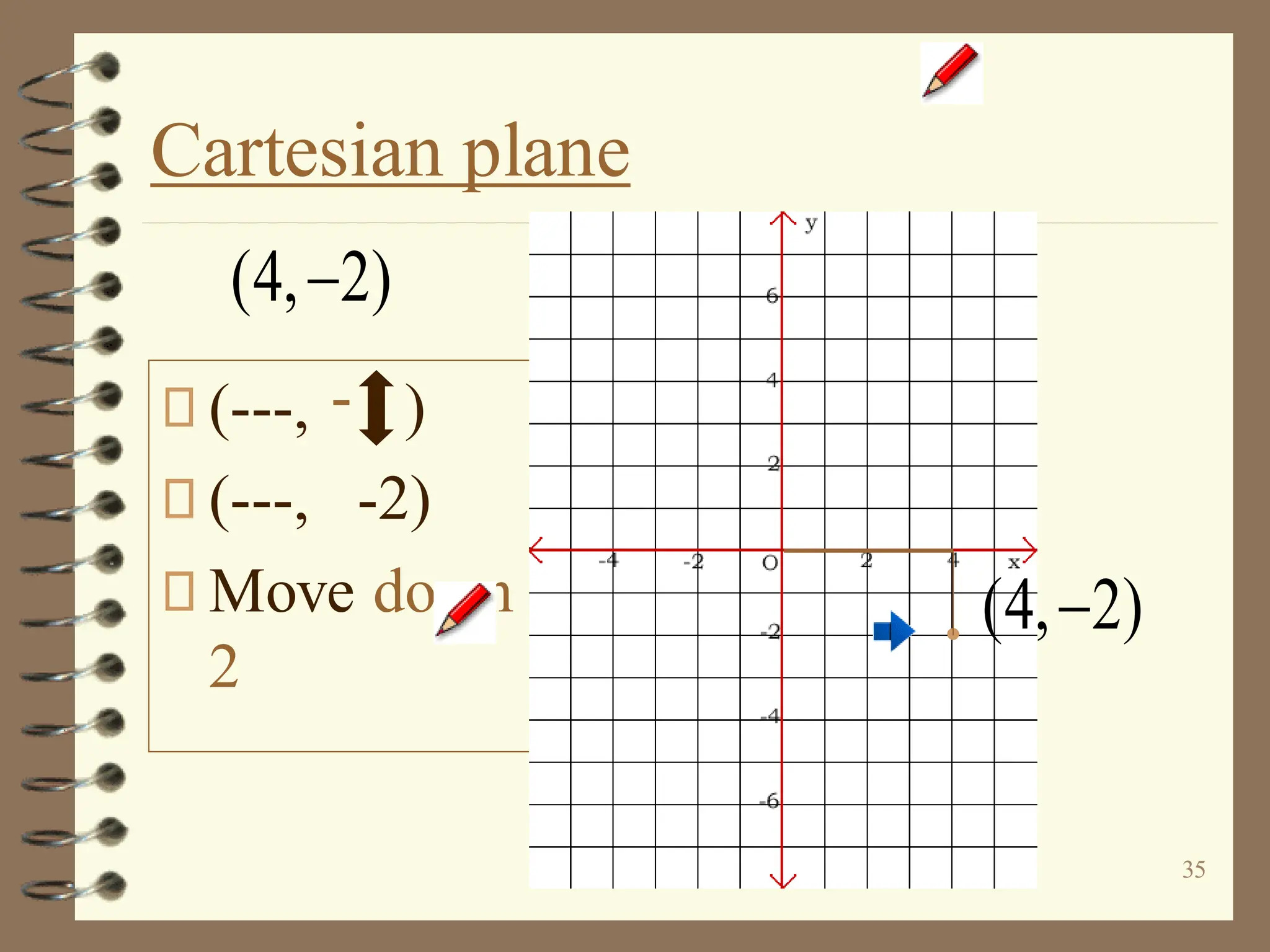
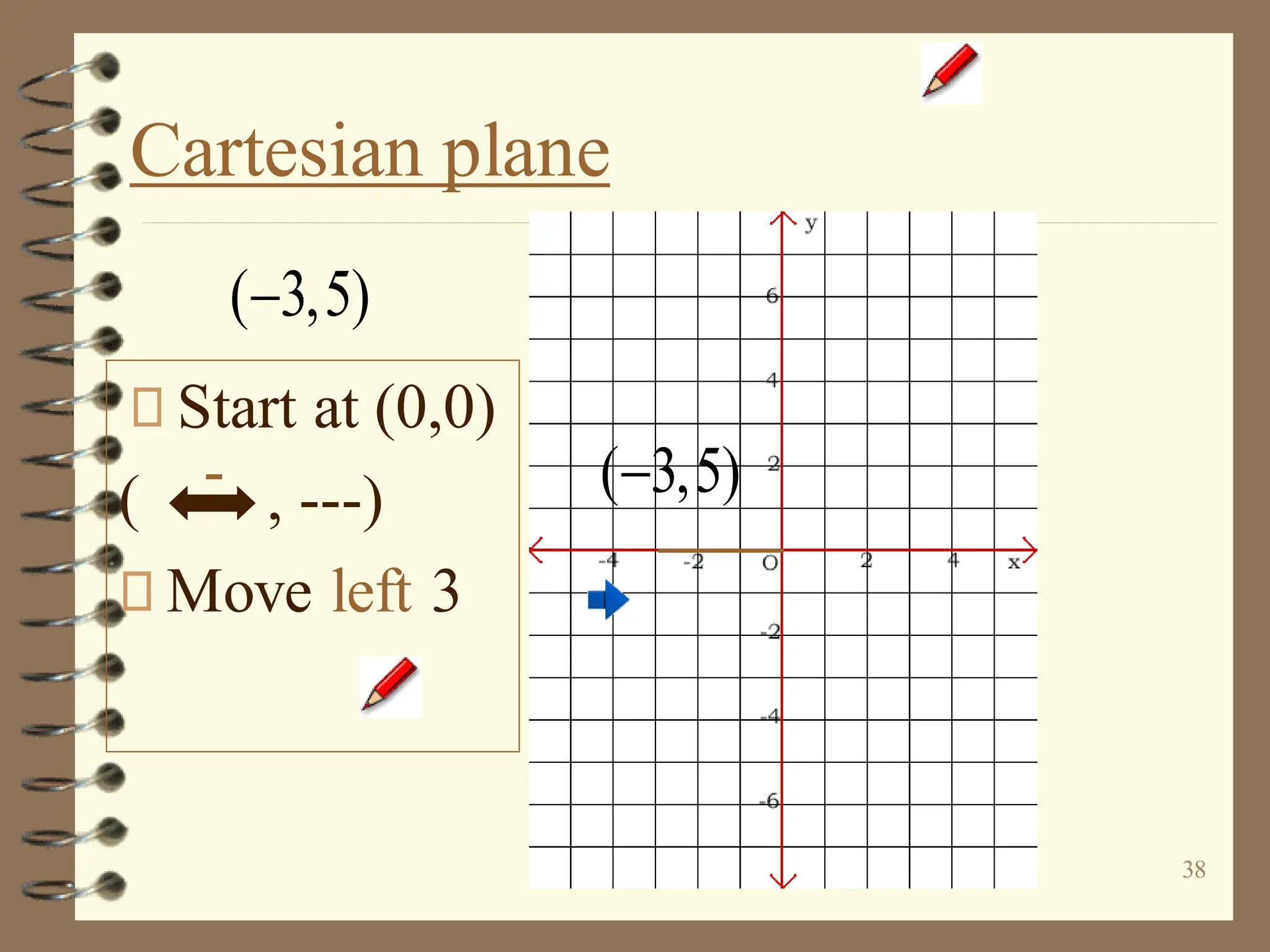
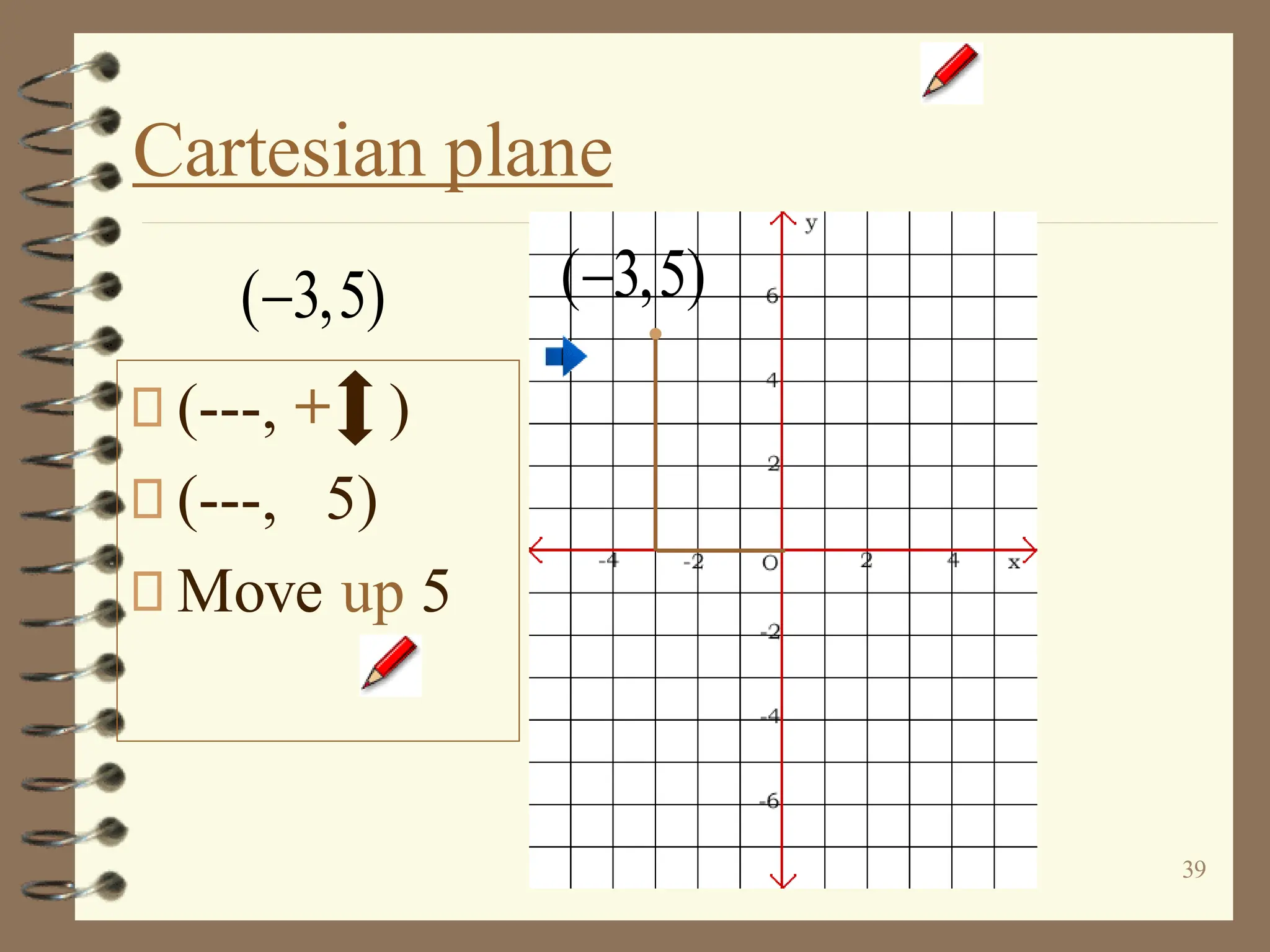
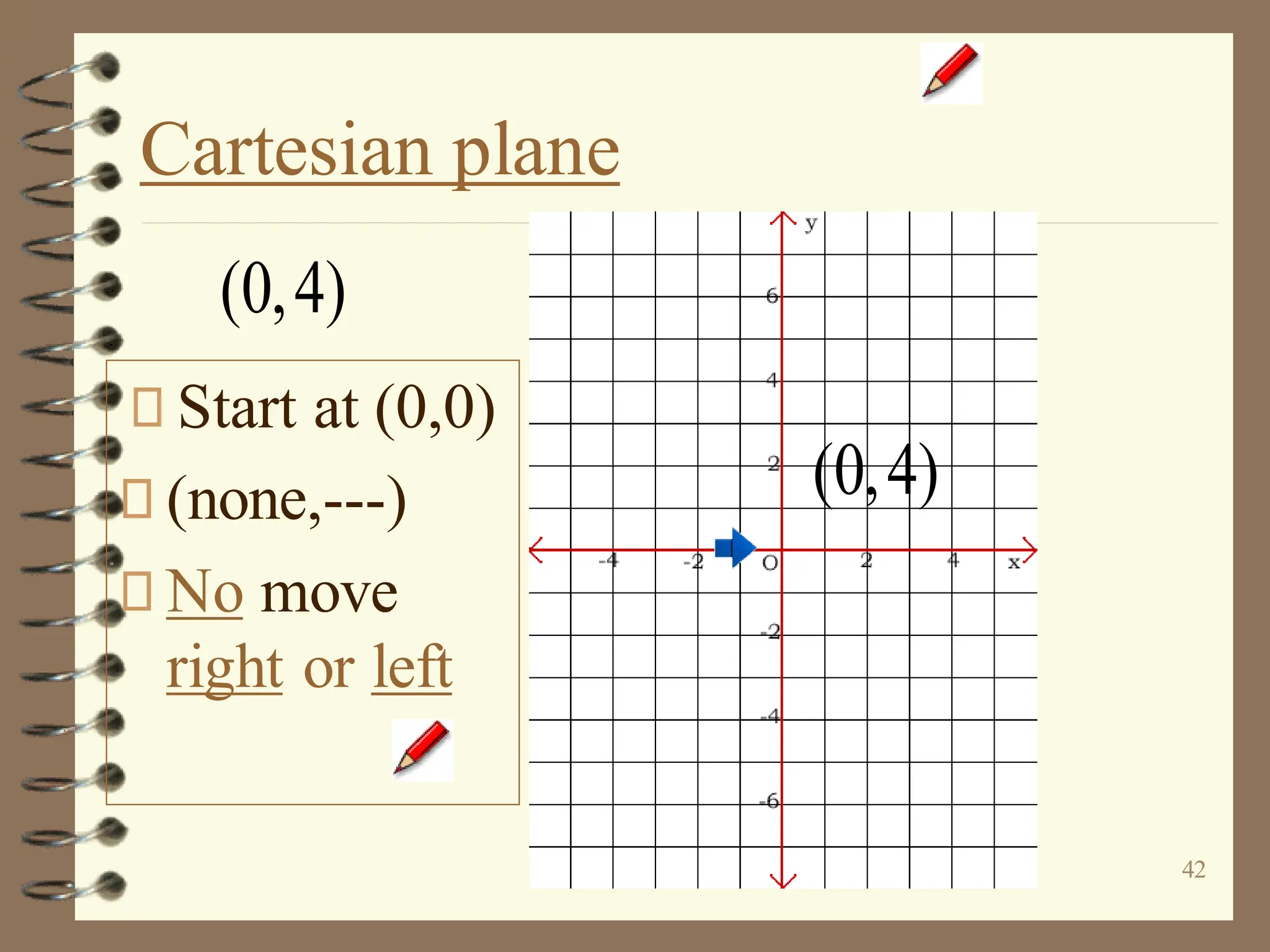
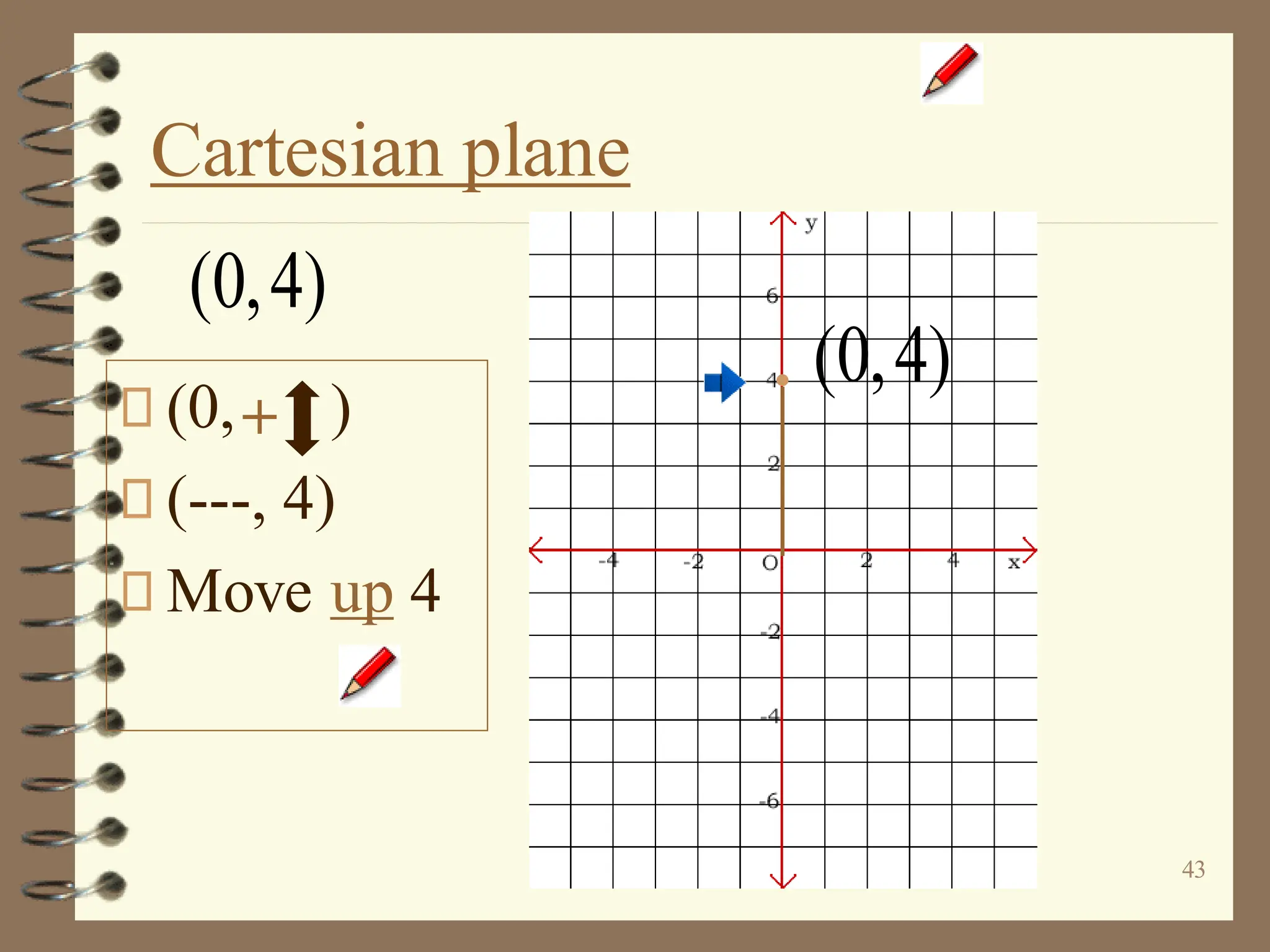
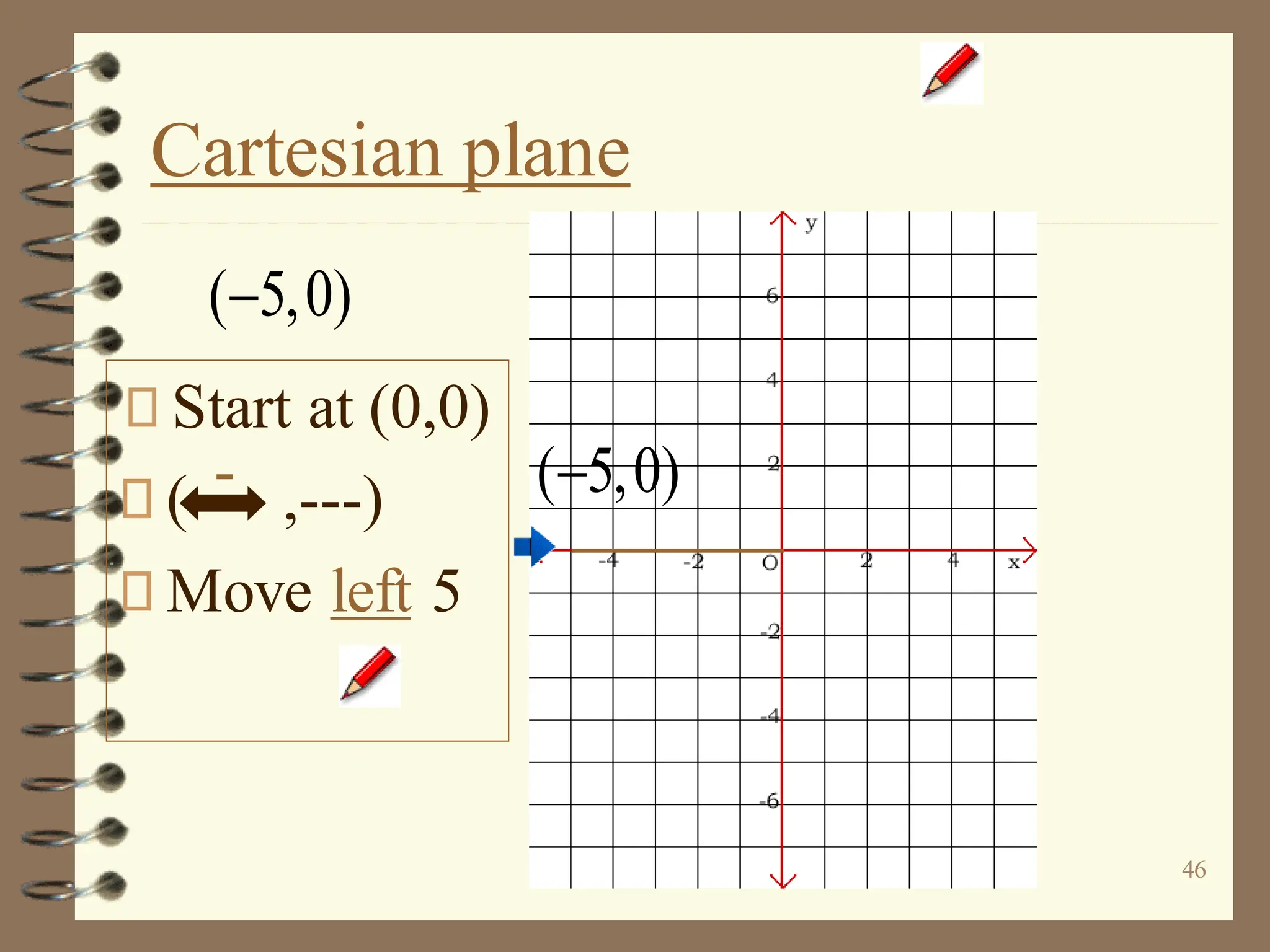
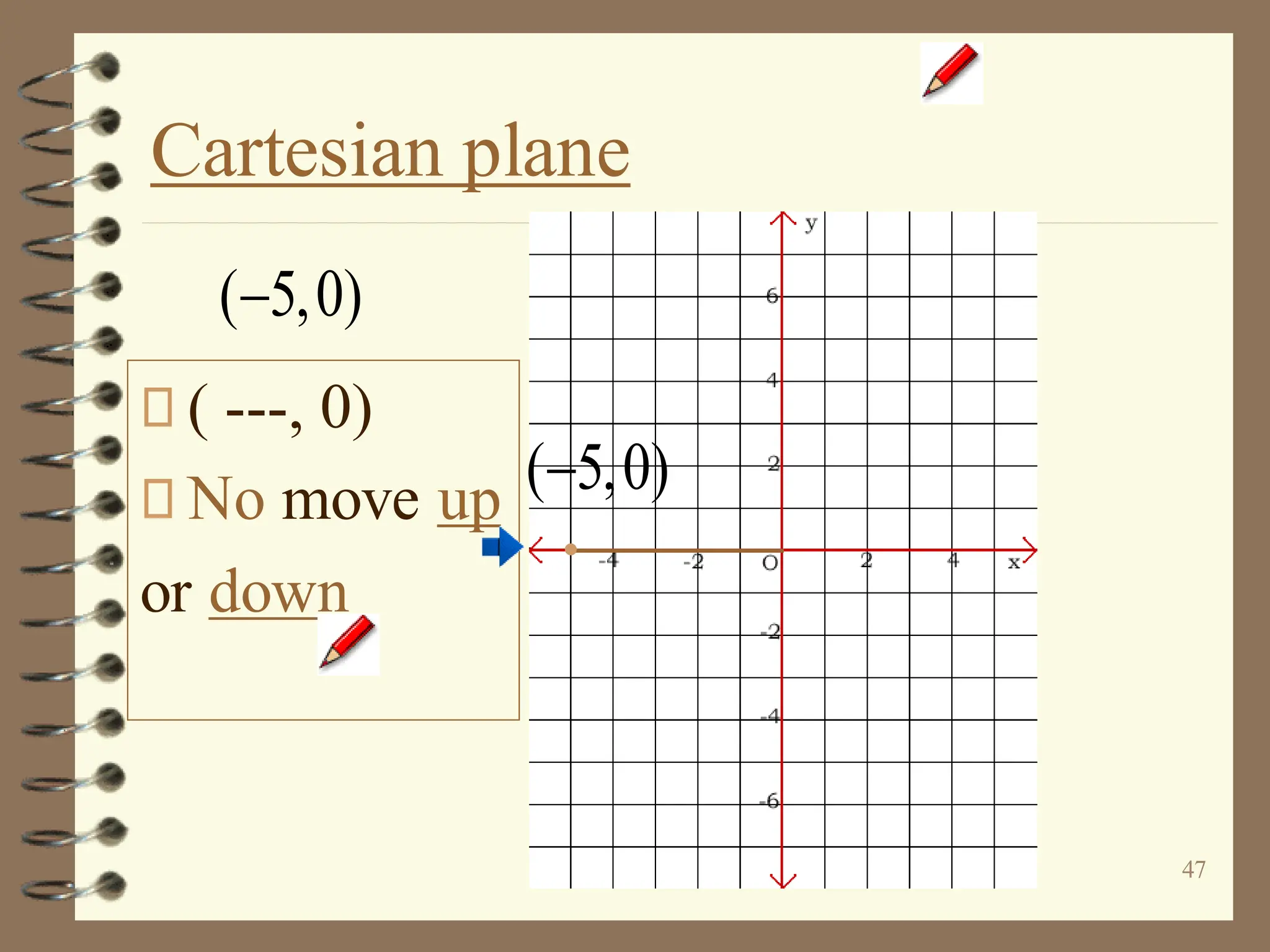
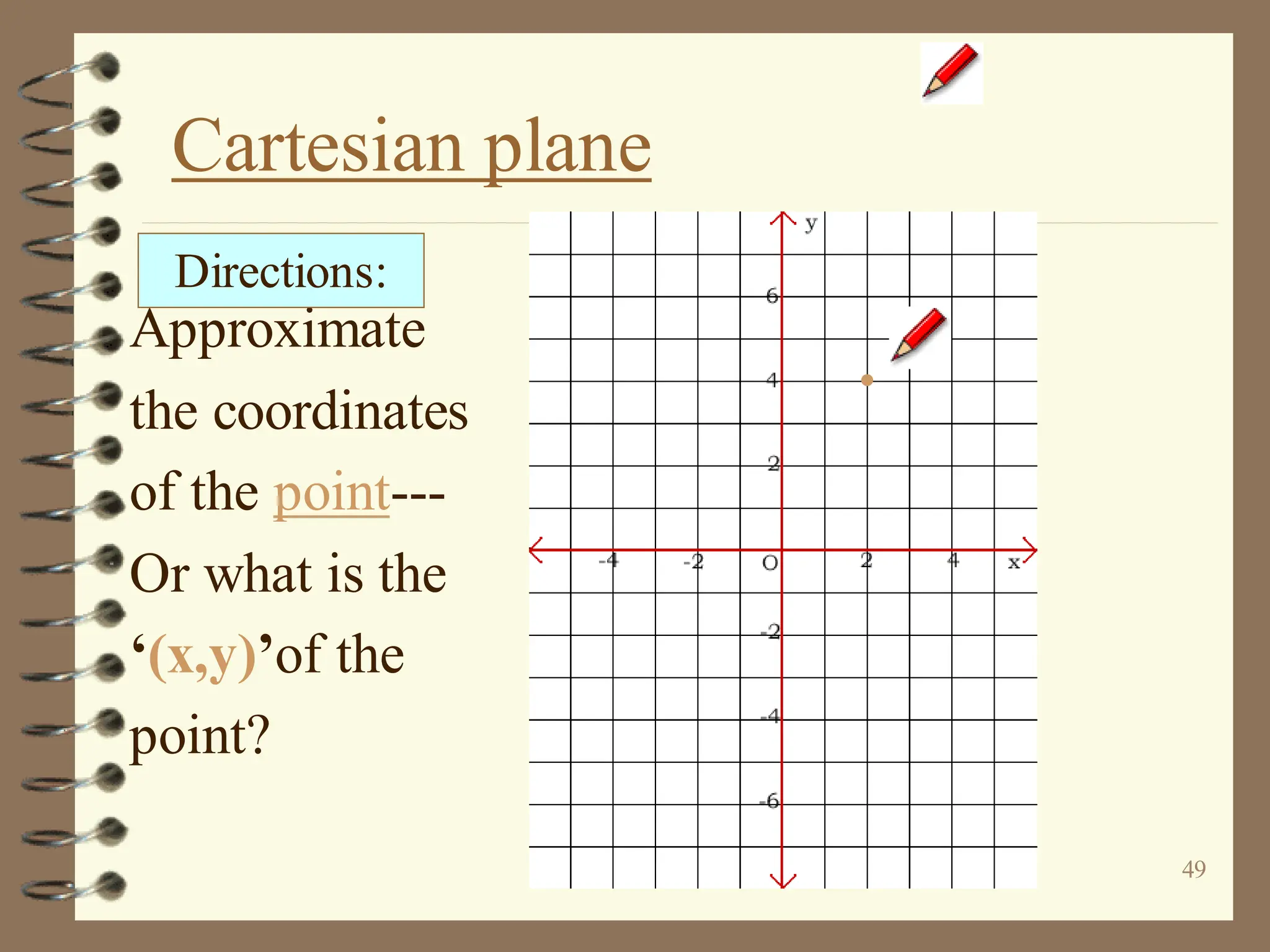
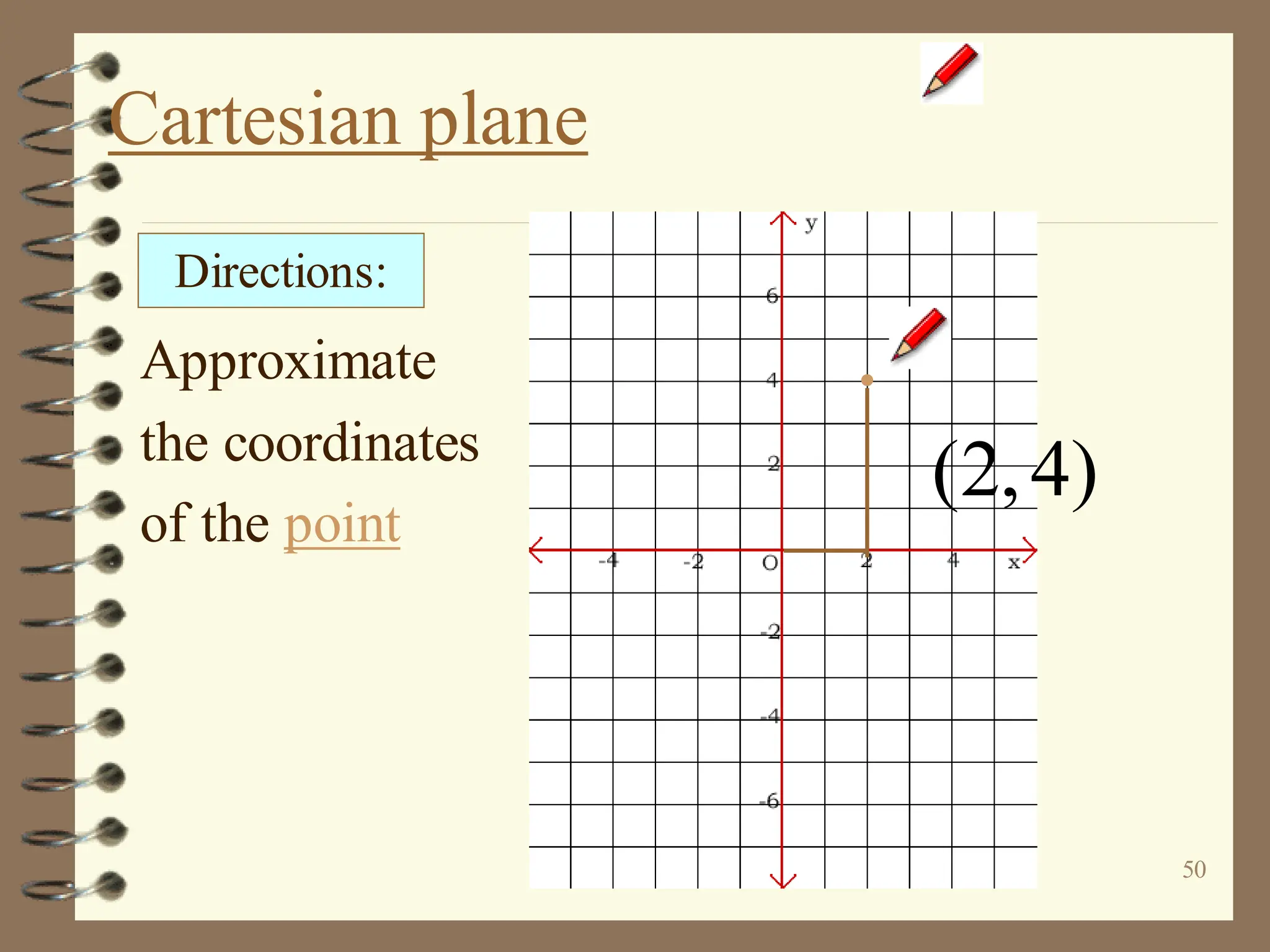
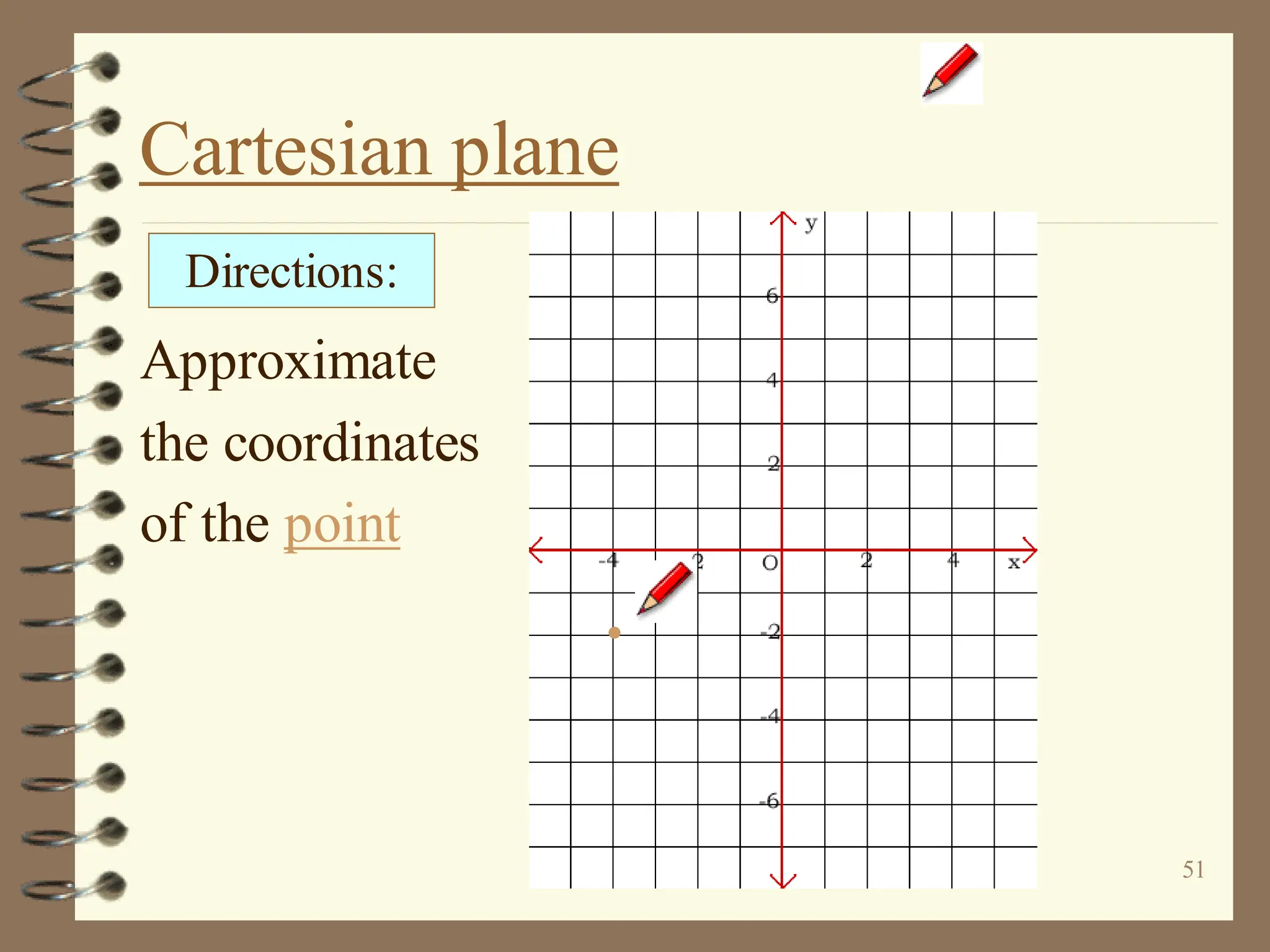
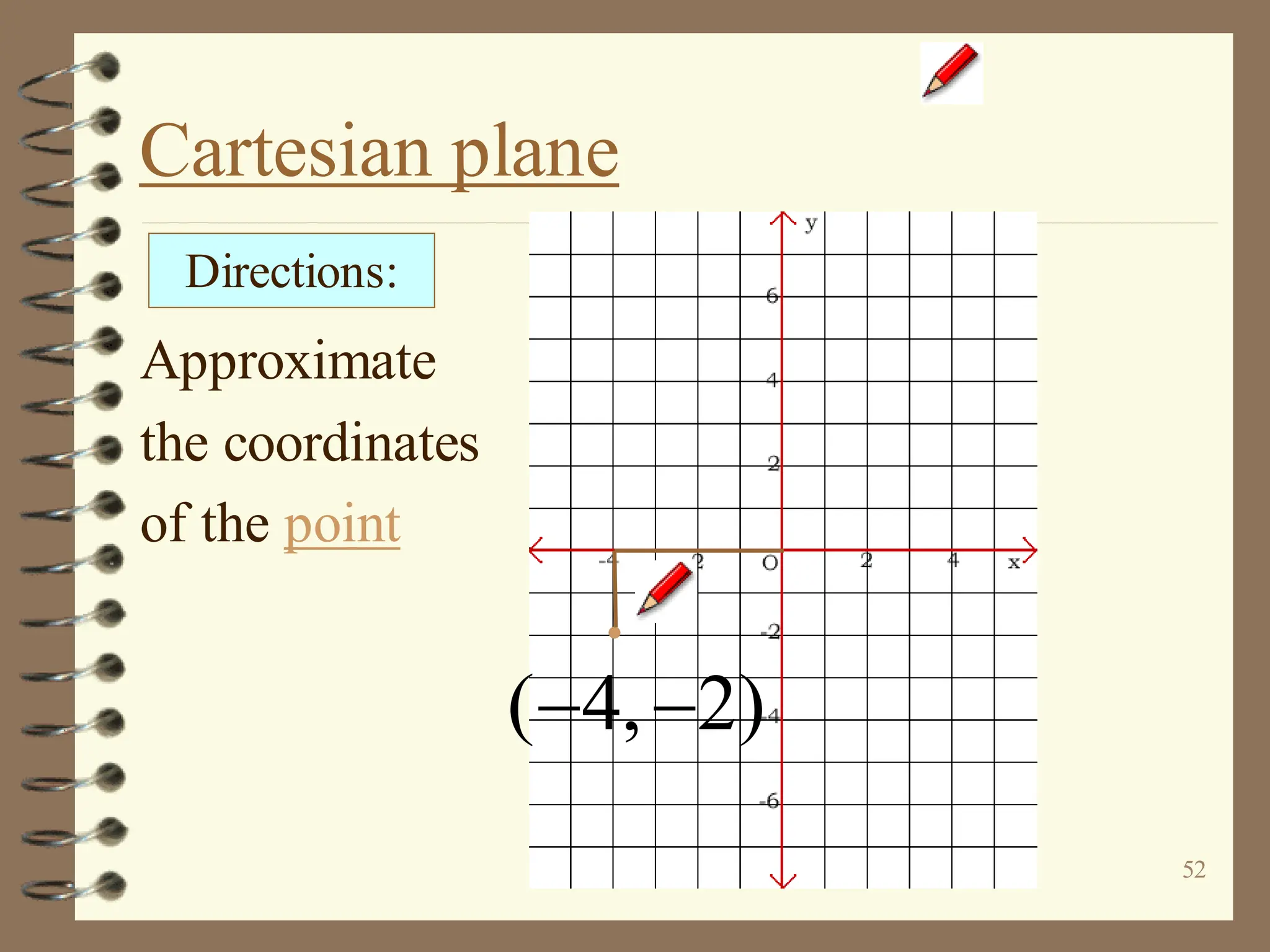
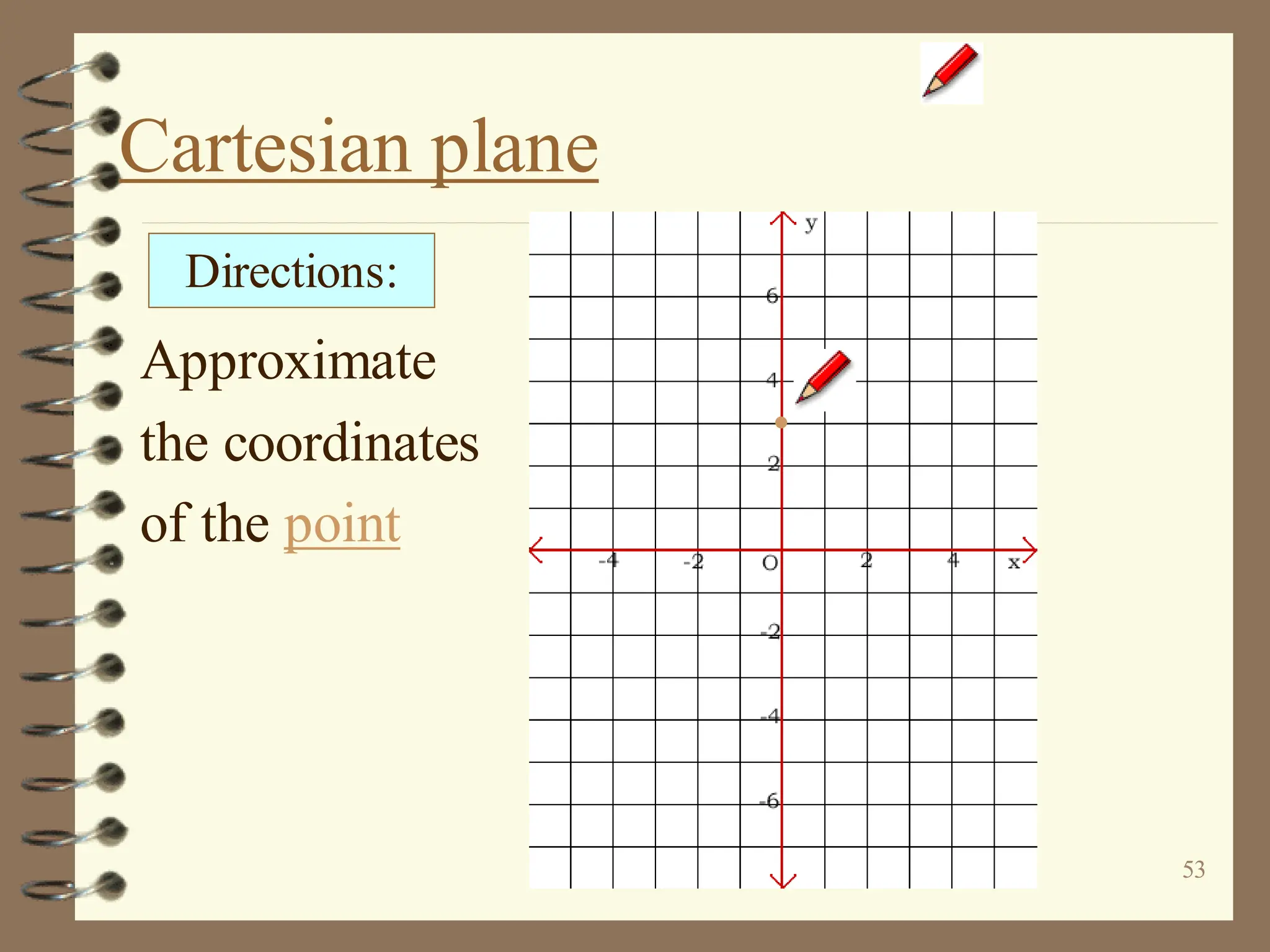
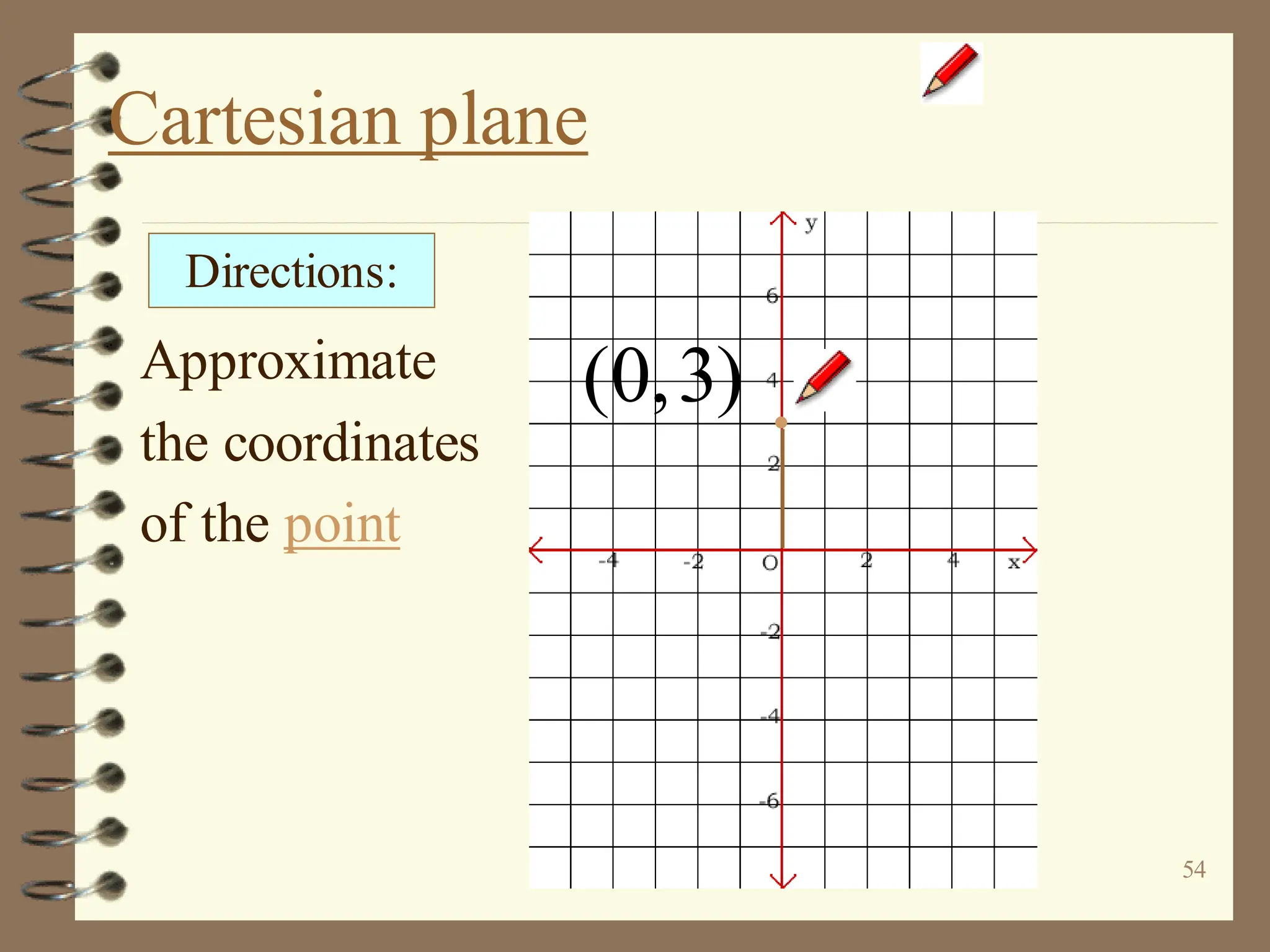
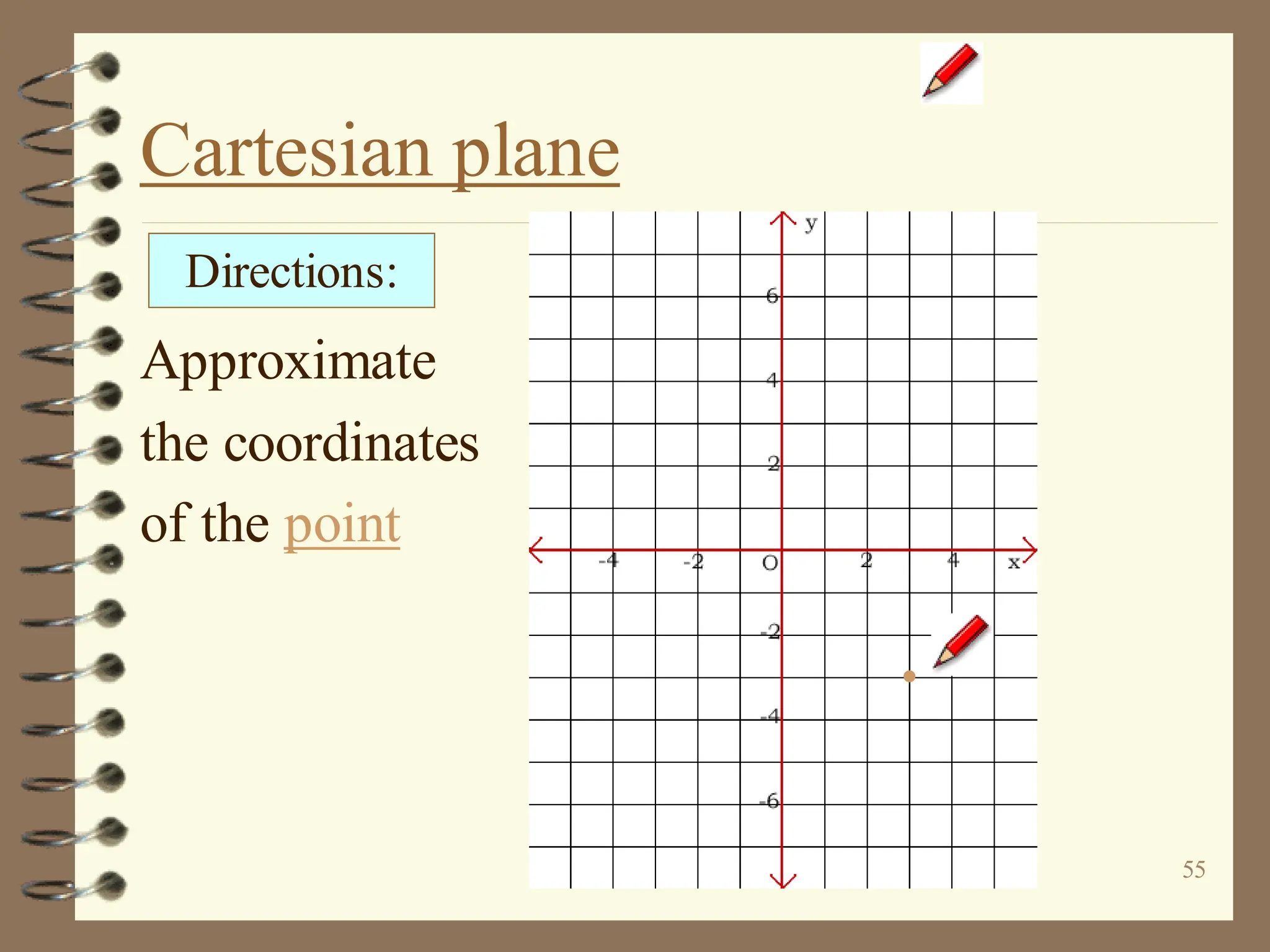
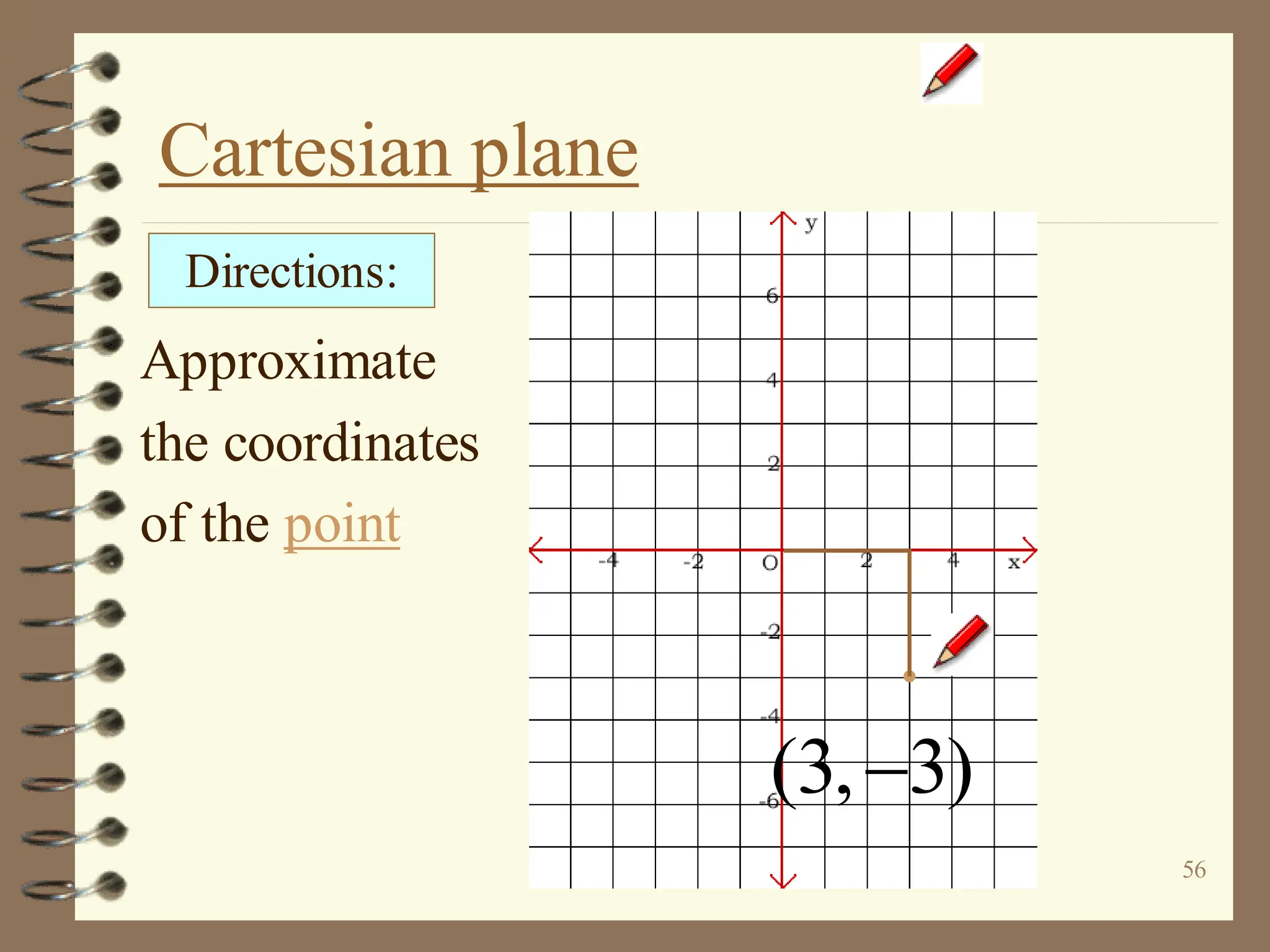
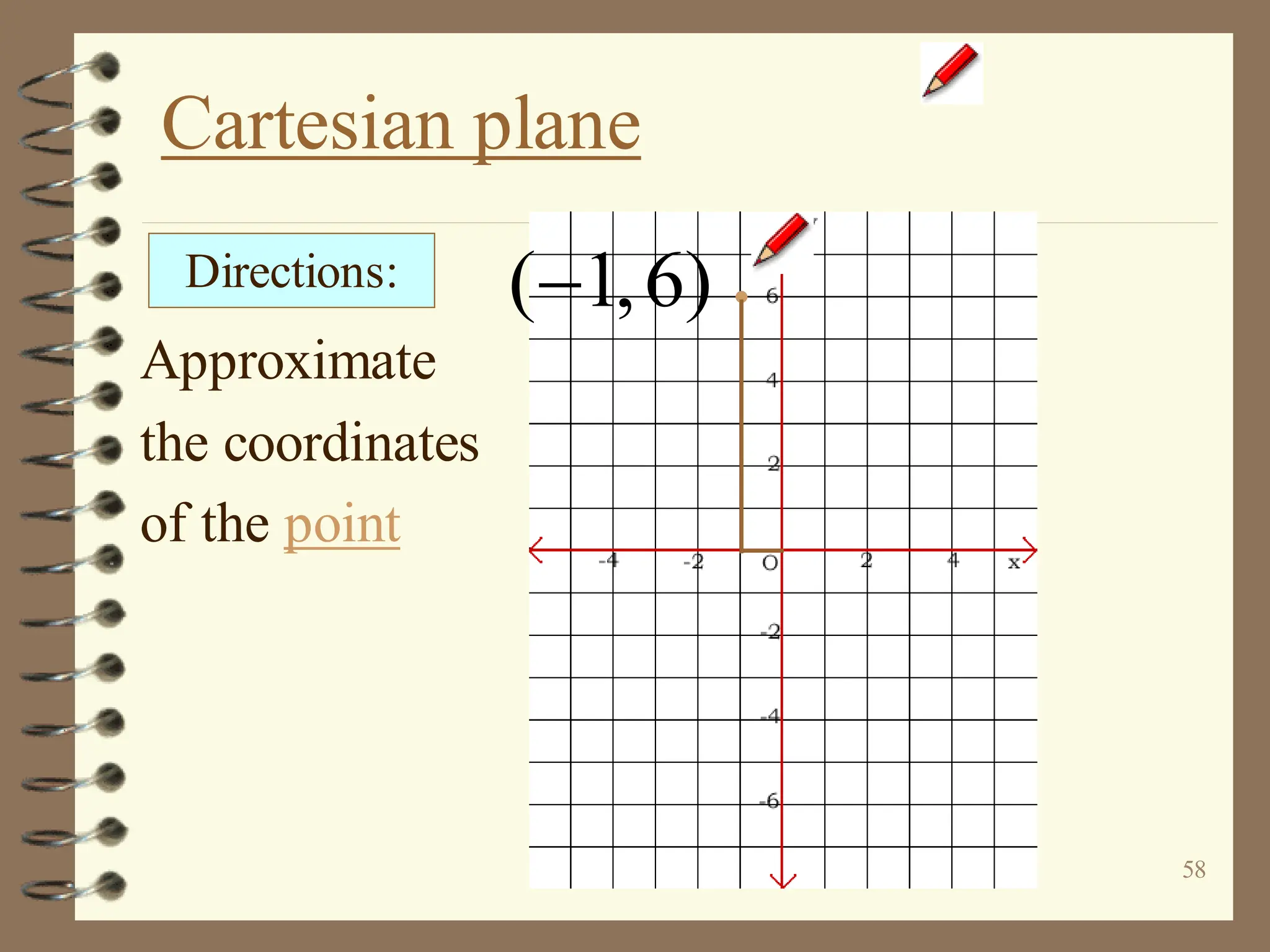
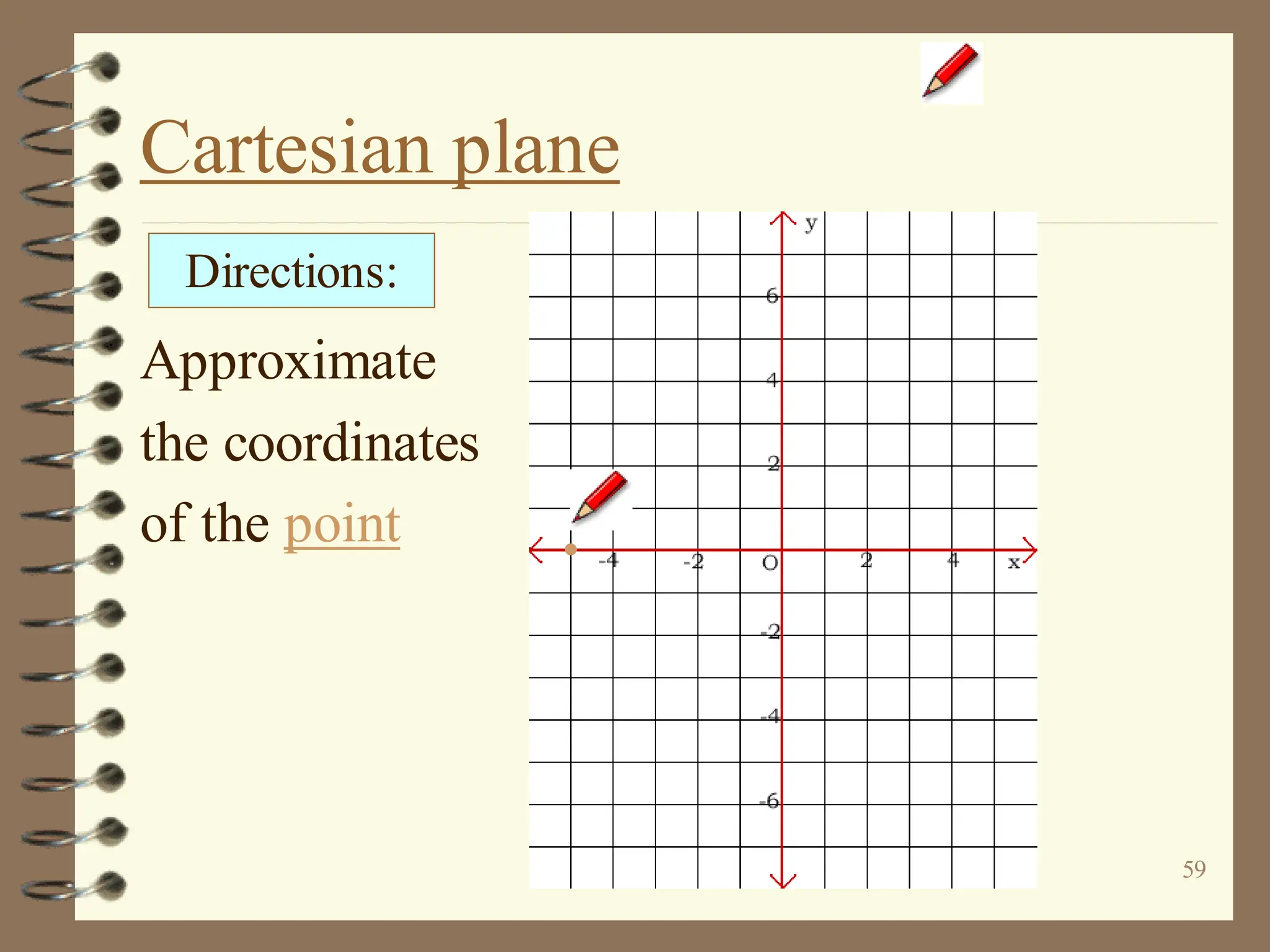
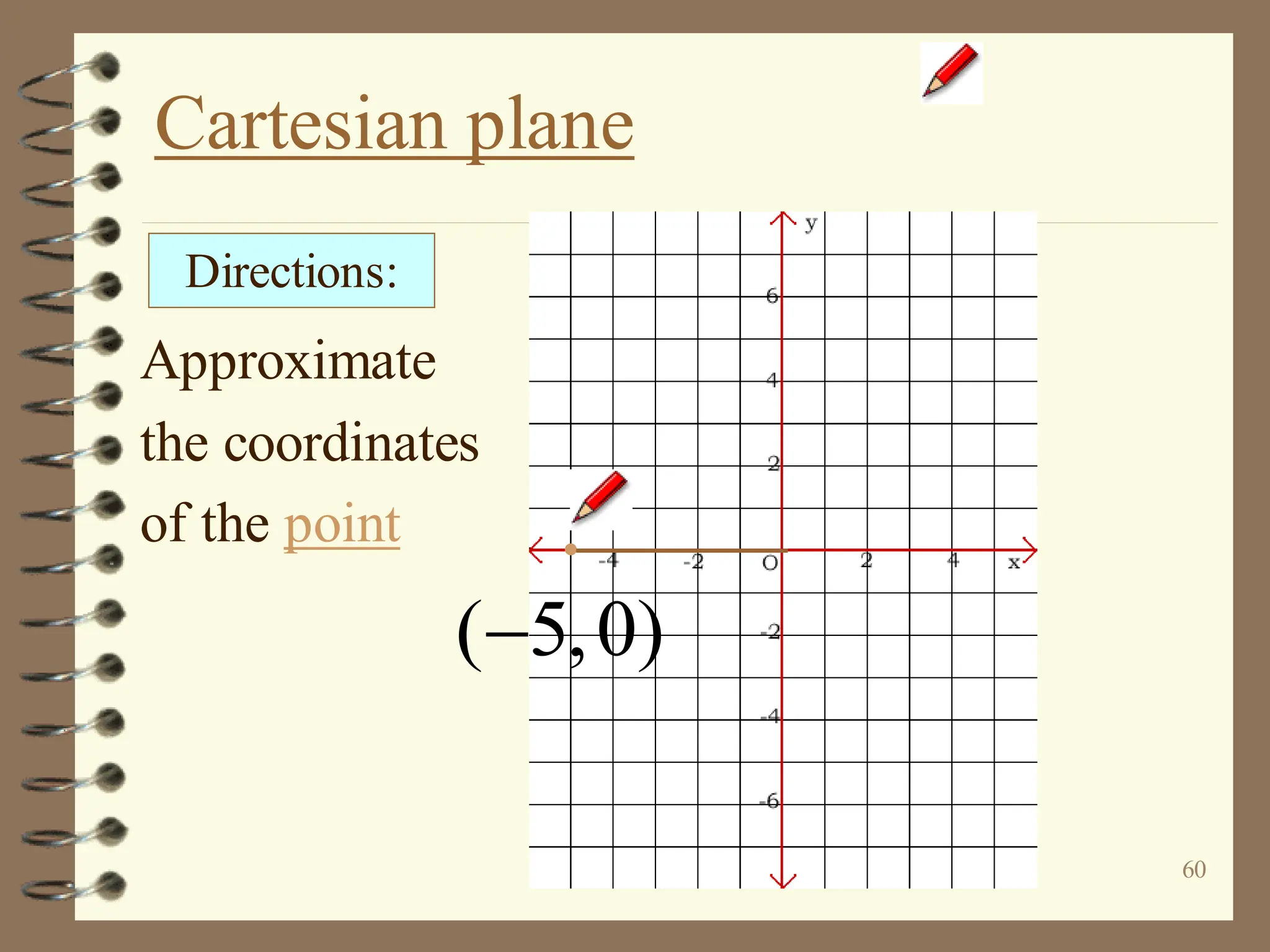
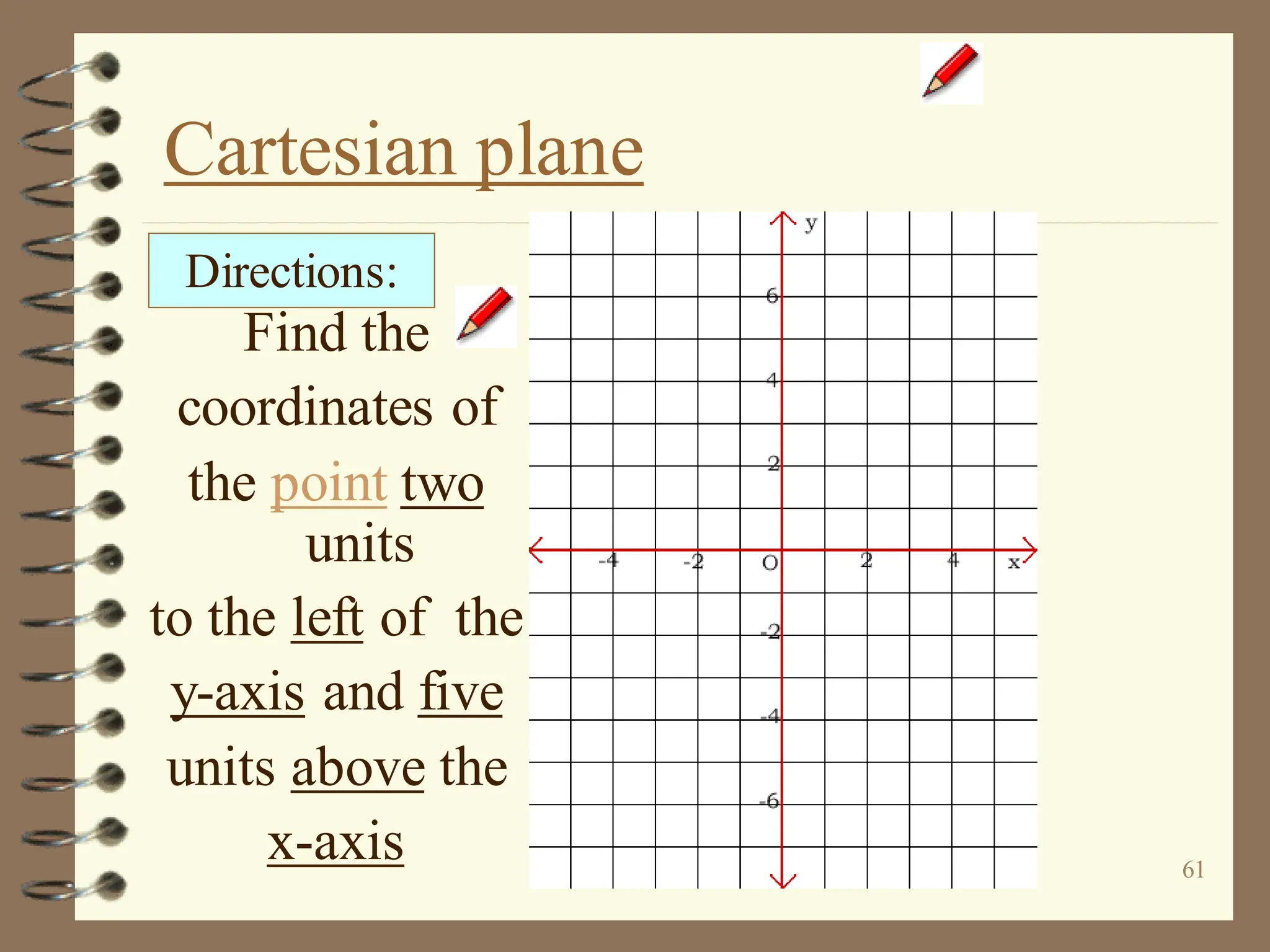
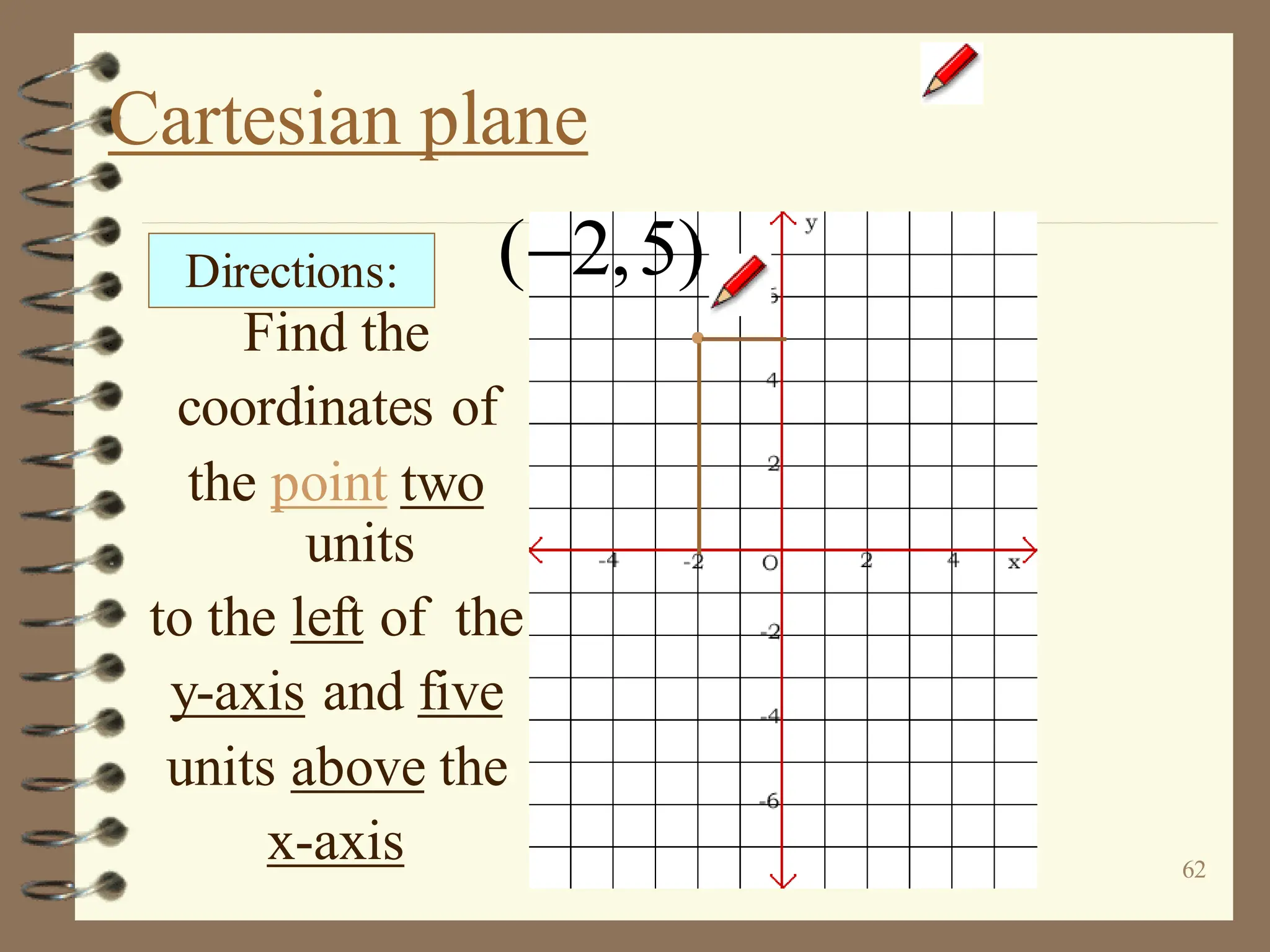
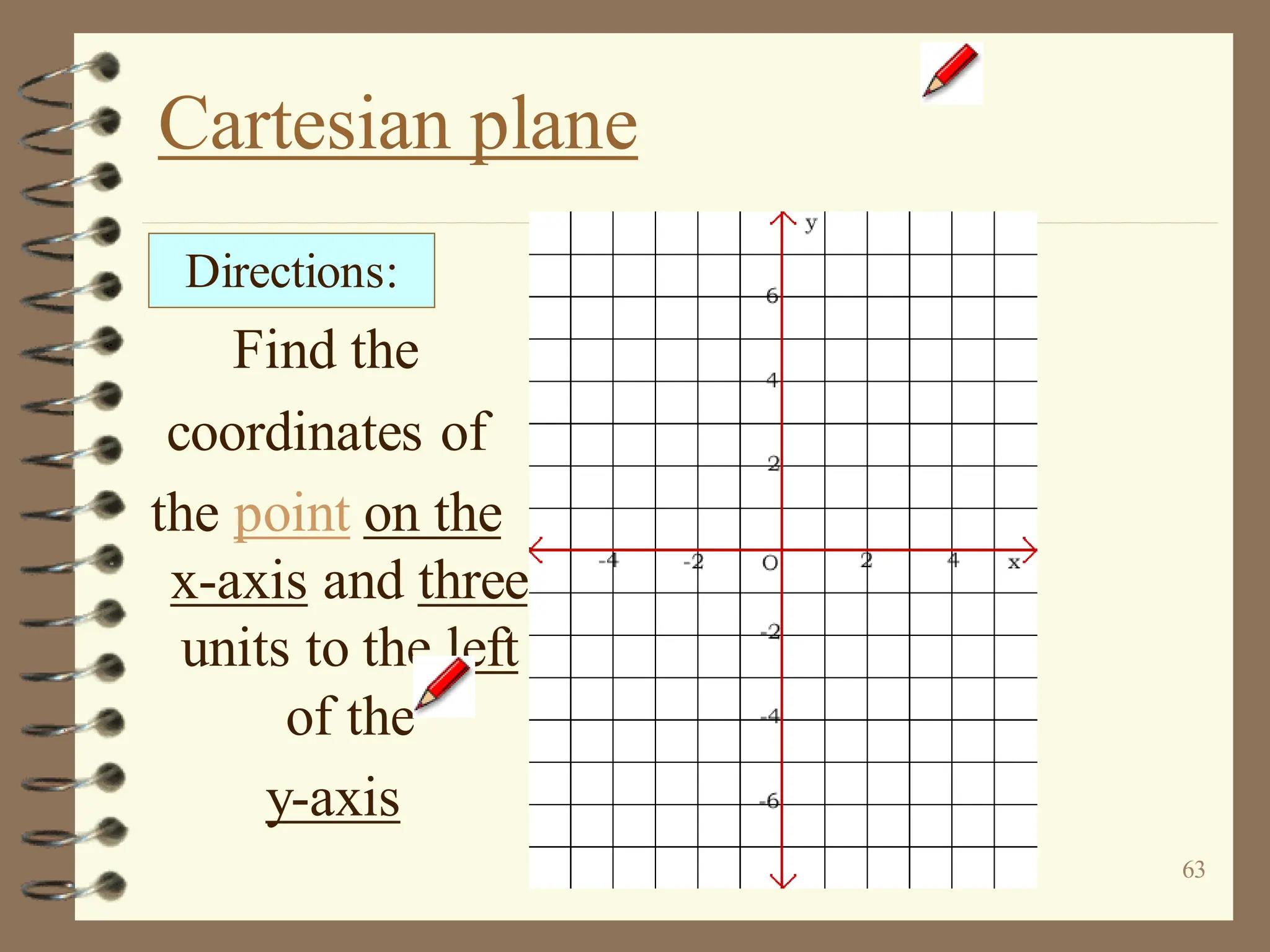
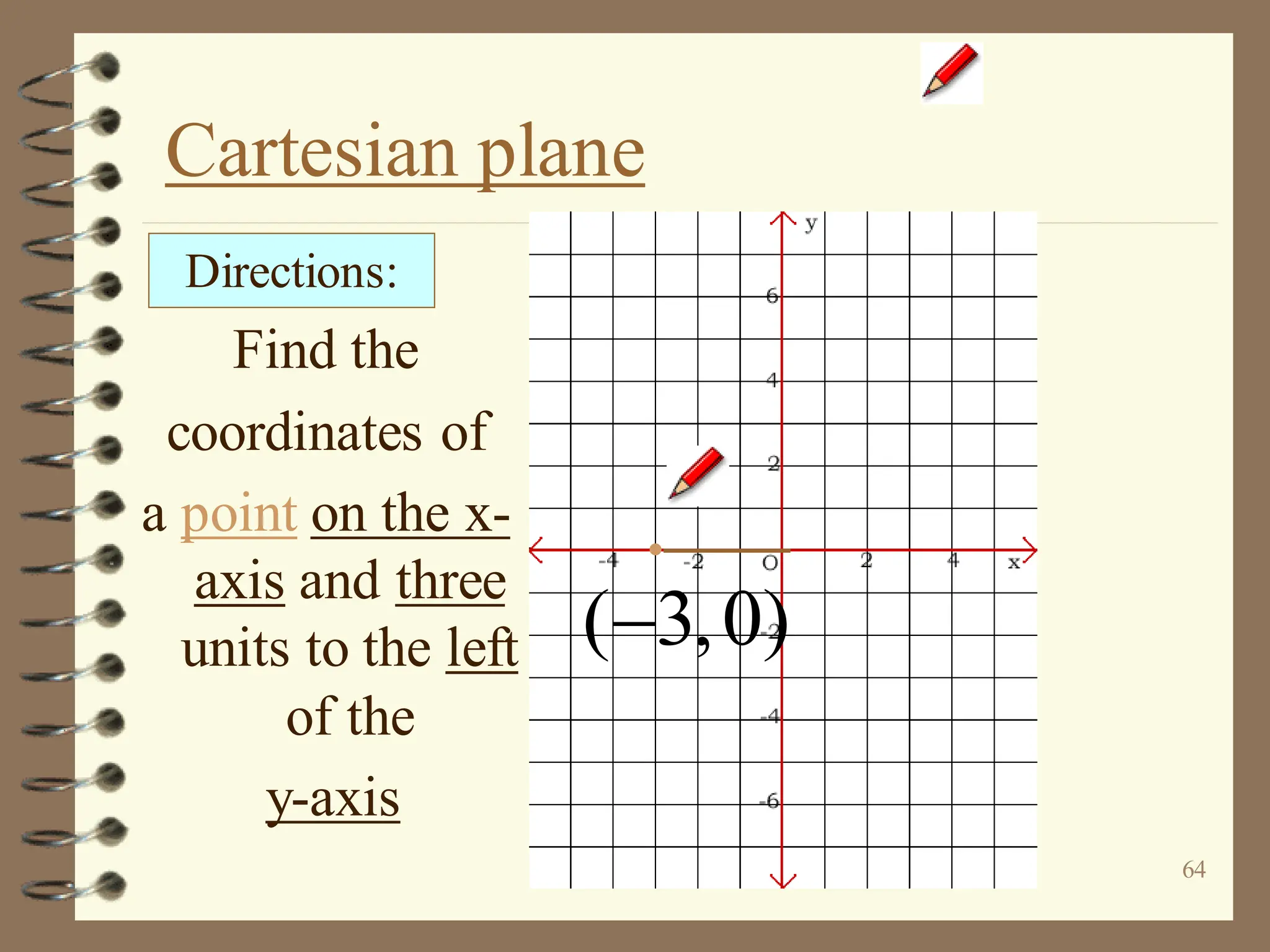
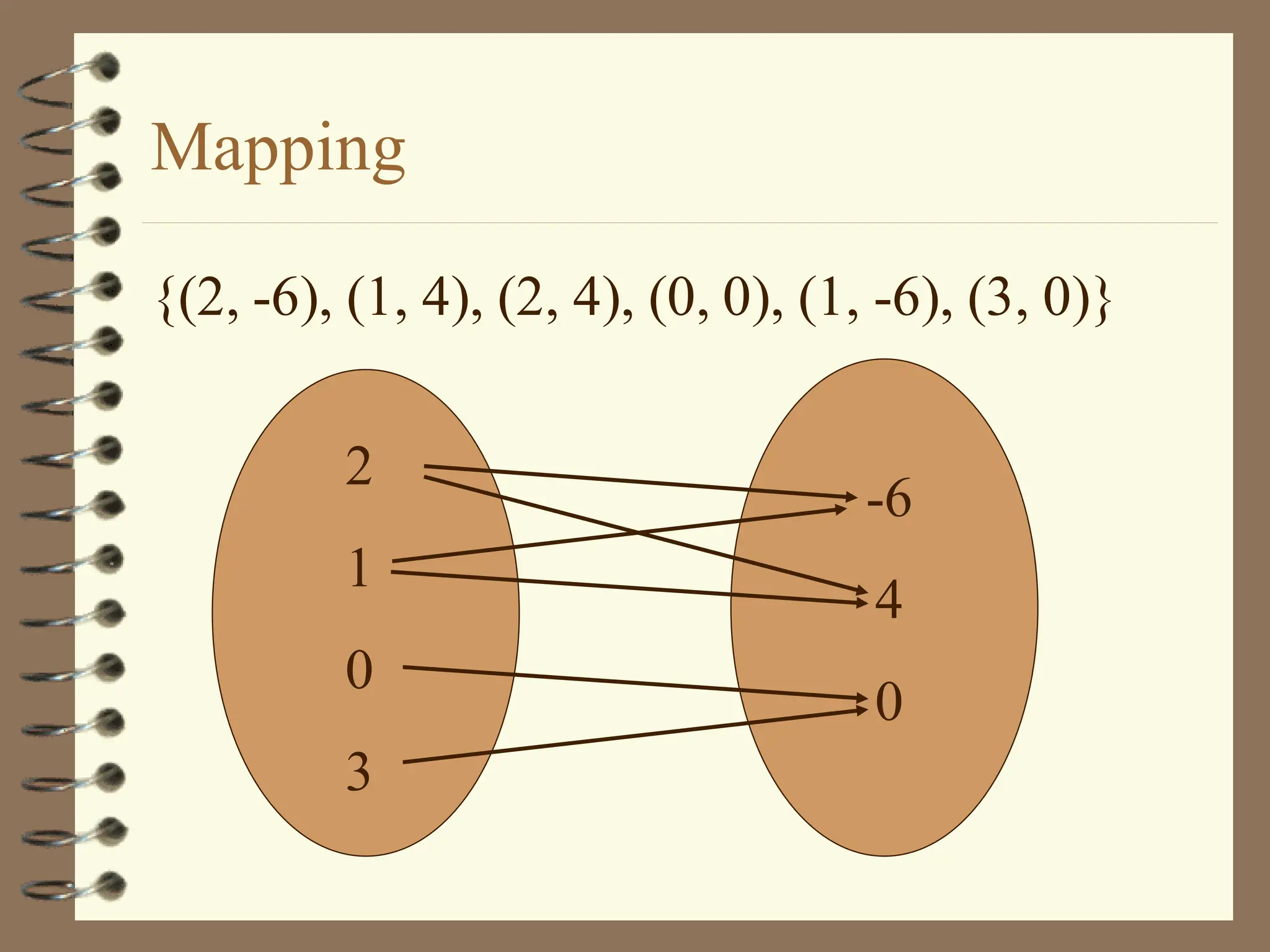
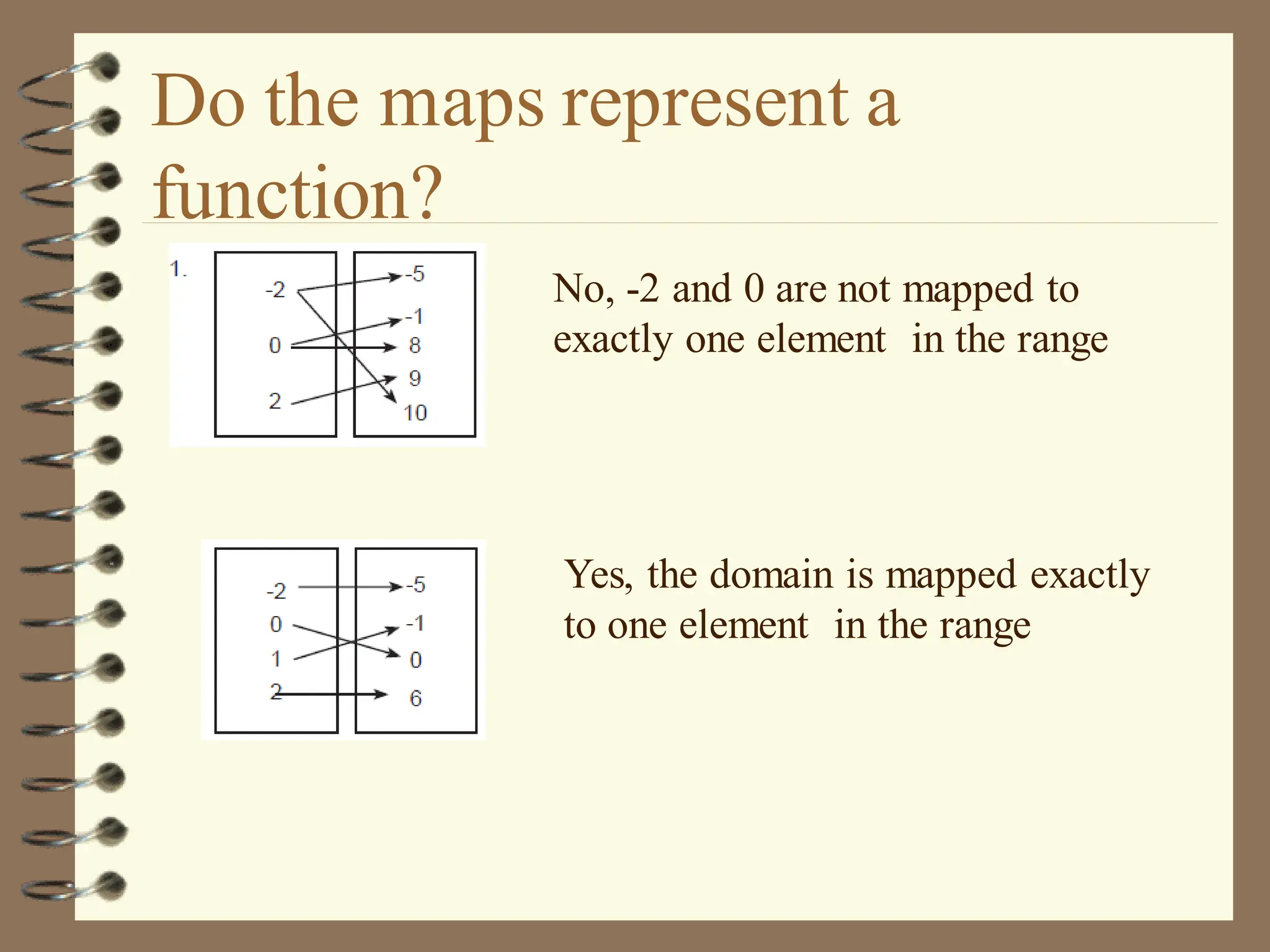
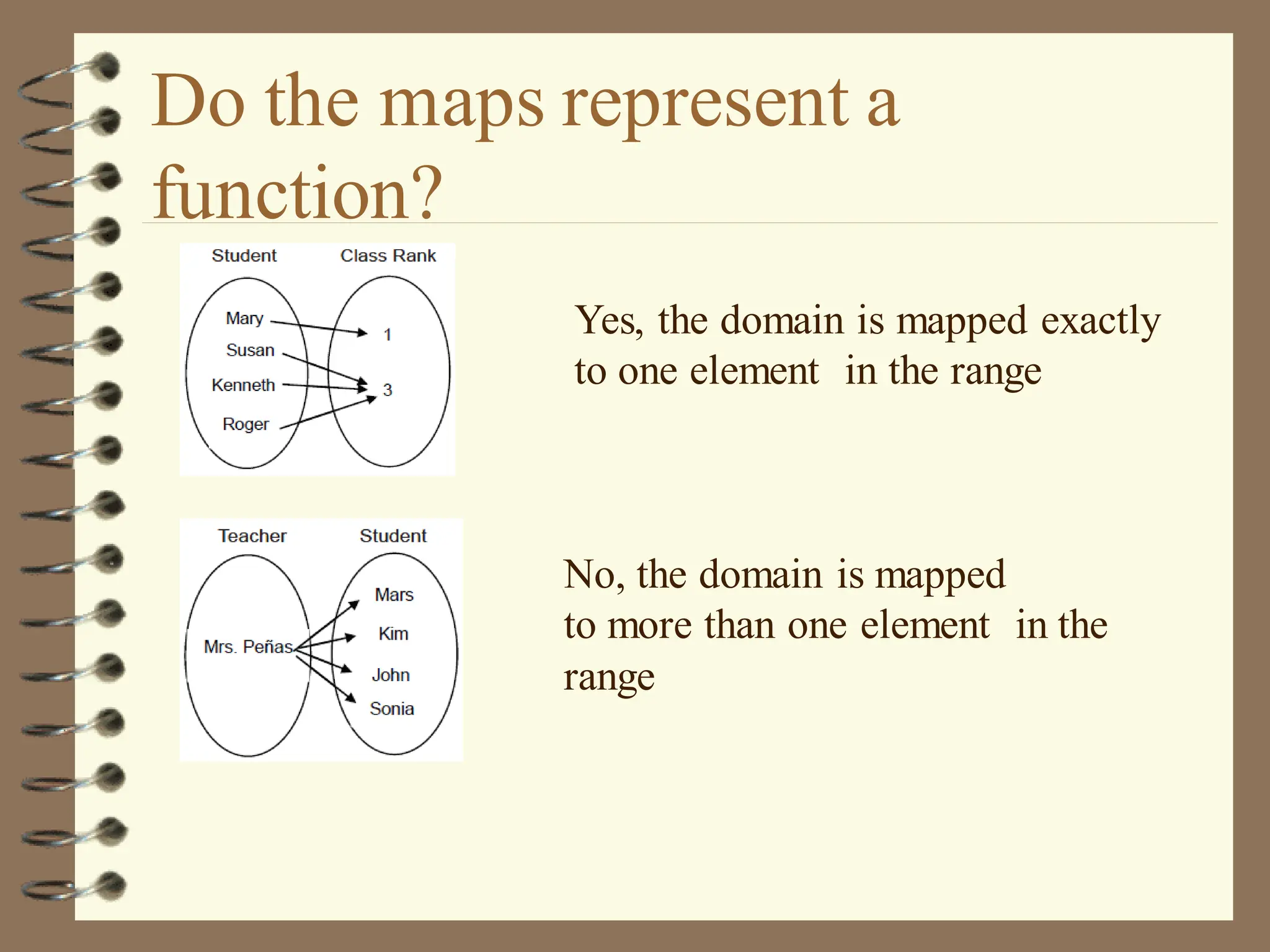
The document discusses the Cartesian coordinate plane and functions. It defines the Cartesian plane as being formed by two perpendicular number lines called the x-axis and y-axis that intersect at the origin point (0,0). Each point on the plane is represented by an ordered pair (x,y) denoting its coordinates. A relation is a set of ordered pairs while a function is a relation where each x-value is mapped to only one y-value. The document provides examples of relations, tables, and mappings to illustrate these concepts.

1. 1
Cartesian Coordinate Plane
First take a look at………….

2. 2
A little history

3. Cartesian Plane

4. 4
Now, let’s take a look at…

5. 5
Cartesian plane
Formed by
intersecting
two
real number
lines at
right angles

6. 6
Cartesian plane
Horizontal
axis is
usually
called the
x-axis

7. 7
Cartesian plane
Vertical
axis is
usually
called the
y-axis

8. 8
Cartesian plane
x-y plane
Also called:

9. 9
Cartesian plane
x-y plane
rectangular
coordinate
system
Also called:

10. 10
Now, let’s take a closer look…

11. 11
Cartesian plane
Divides into
Quadrants

12. 12
Cartesian plane
I

13. 13
Cartesian plane
I
II

14. 14
Cartesian plane
I
II
III

15. 15
Cartesian plane
I
II
III IV

16. 16
Cartesian plane
I
II
III IV

17. 17
Cartesian plane
The
intersection
of the two
axes is
called the
origin

18. 18
Cartesian plane
Math Alert
The
quadrants
do not
include the
axes
I
II
III IV

19. 19
Cartesian plane
Math Alert
A point on the
x or y axis is
not in a
quadrant
I
II
III IV

20. 20
Cartesian plane
Each point in
the
x-y plane is
associated
with an
ordered
pair, (x,y)
(x,y)
(x,y)
(x,y)
(x,y)

21. 21
The x and y of
the ordered
pair,
(x,y), are called
its
coordinates
Cartesian plane
(x,y)
(x,y)
(x,y)
(x,y)

22. 22
Math Alert
There is an
infinite
amount of
points in the
Cartesian
plane
Cartesian plane

23. 23
Take note of these graphing
basics

24. 24
Always start
at (0,0)---every
point
“originates” at
the origin
Cartesian plane

25. 25
In plotting (x,y)
---remember the
directions of
both the x and y
axis
Cartesian plane y
x

26. 26
Cartesian plane
(x,---)
x-axis goes
left and right

27. 27
Cartesian plane
(---,y)
y-axis goes
up and down

28. 28
Now, let’s look at plotting…

29. 29
Now, let’s look at plotting…
(2,1)

30. 30
Cartesian plane
Start at (0,0)
( , ---)
Move right
2
(2,1)
+
(2,1)

31. 31
Cartesian plane
(---, )
(---, 1)
Move up 1
(2,1)
+
(2,1)

32. 32
Now, let’s look at plotting…

33. 33
Now, let’s look at plotting…
(4, 2)
−

34. 34
Cartesian plane
Start at (0,0)
( , ---)
Move right 4
+
(4, 2)
−
(4, 2)
−

35. 35
Cartesian plane
(---, )
(---, -2)
Move down
2
(4, 2)
−
-
(4, 2)
−

36. 36
Now, let’s look at plotting…

37. 37
Now, let’s look at plotting …
( 3,5)
−

38. 38
Cartesian plane
Start at (0,0)
( , ---)
Move left 3
( 3,5)
−
-
( 3,5)
−

39. 39
Cartesian plane
(---, )
(---, 5)
Move up 5
+
( 3,5)
−
( 3,5)
−

40. 40
Now, let’s look at plotting …

41. 41
Now, let’s look at plotting …
(0,4)

42. 42
Cartesian plane
Start at (0,0)
(none,---)
No move
right or left
(0,4)
(0,4)

43. 43
Cartesian plane
(0, )
(---, 4)
Move up 4
+
(0,4)
(0,4)

44. 44
Now, let’s look at plotting …

45. 45
Now, let’s look at plotting …
( 5,0)
−

46. 46
Cartesian plane
Start at (0,0)
( ,---)
Move left 5
( 5,0)
−
( 5,0)
−
-

47. 47
Cartesian plane
( ---, 0)
No move up
or down
( 5,0)
−
( 5,0)
−

48. 48
Now, let’s look at a little plotting
practice…

49. 49
Cartesian plane
Approximate
the coordinates
of the point---
Or what is the
‘(x,y)’of the
point?
Directions:

50. 50
Cartesian plane
Approximate
the coordinates
of the point
Directions:
(2,4)

51. 51
Cartesian plane
Approximate
the coordinates
of the point
Directions:

52. 52
Cartesian plane
Approximate
the coordinates
of the point
Directions:
( 4, 2)
− −

53. 53
Cartesian plane
Approximate
the coordinates
of the point
Directions:

54. 54
Cartesian plane
Approximate
the coordinates
of the point
Directions:
(0,3)

55. 55
Cartesian plane
Approximate
the coordinates
of the point
Directions:

56. 56
Cartesian plane
Approximate
the coordinates
of the point
Directions:
(3, 3)
−

57. 57
Cartesian plane
Approximate
the coordinates
of the point
Directions:

58. 58
Cartesian plane
Approximate
the coordinates
of the point
Directions: ( 1,6)
−

59. 59
Cartesian plane
Approximate
the coordinates
of the point
Directions:

60. 60
Cartesian plane
Approximate
the coordinates
of the point
Directions:
( 5,0)
−

61. 61
Cartesian plane
Find the
coordinates of
the point two
units
to the left of the
y-axis and five
units above the
x-axis
Directions:

62. 62
Cartesian plane
Find the
coordinates of
the point two
units
to the left of the
y-axis and five
units above the
x-axis
Directions: ( 2,5)
−

63. 63
Cartesian plane
Find the
coordinates of
the point on the
x-axis and three
units to the left
of the
y-axis
Directions:

64. 64
Cartesian plane
Find the
coordinates of
a point on the x-
axis and three
units to the left
of the
y-axis
Directions:
( 3,0)
−

65. Hanapin Mo ‘ko

66. 66
Lesson 2: Representations of
Relations and Functions

67. Relations & Functions
Relation: a set of ordered pairs
Domain: the set of x-coordinates
Range: the set of y-coordinates
When writing the domain and range, do not
repeat values.

68. Relations and Functions
Given the relation:
{(2, -6), (1, 4), (2, 4), (0,0), (1, -6), (3, 0)}
State the domain:
D: {0,1, 2, 3}
State the range:
R: {-6, 0, 4}

69. Relations and Functions
• Relations can be written in
several ways: ordered pairs,
table, graph, or mapping.

70. Table
{(3, 4), (7, 2), (0, -1),
(-2, 2), (-5, 0), (3, 3)}
x y
3 4
7 2
0 -1
-2 2
-5 0
3 3

71. Mapping
• Create two ovals with the domain on
the left and the range on the right.
• Elements are not repeated.
• Connect elements of the domain with
the corresponding elements in the
range by drawing an arrow.

72. Mapping
{(2, -6), (1, 4), (2, 4), (0, 0), (1, -6), (3, 0)}
2
1
0
3
-6
4
0

73. Functions
• A function is a relation in which the
members of the domain (x-values)
DO NOT repeat.
• So, for every x-value there is only
one y-value that corresponds to it.
• y-values can be repeated.

74. Do the ordered pairs represent a
function?
{(3, 4), (7, 2), (0, -1), (-2, 2), (-5, 0), (3, 3)}
No, 3 is repeated in the domain.
{(4, 1), (5, 2), (8, 2), (9, 8)}
Yes, no x-coordinate is repeated.

75. Do the maps represent a
function?
No, -2 and 0 are not mapped to
exactly one element in the range
Yes, the domain is mapped exactly
to one element in the range

76. Do the maps represent a
function?
No, the domain is mapped
to more than one element in the
range
Yes, the domain is mapped exactly
to one element in the range