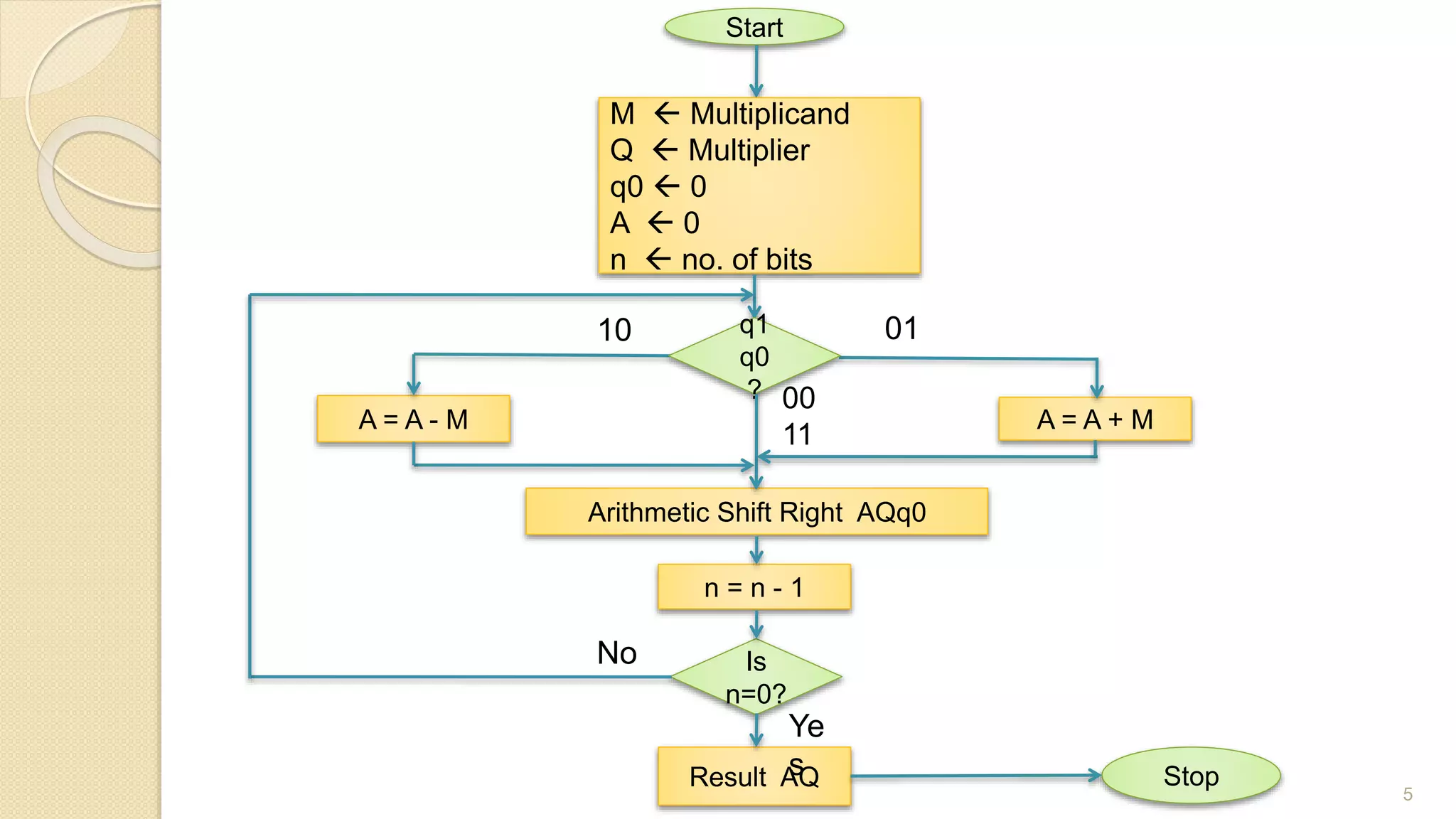
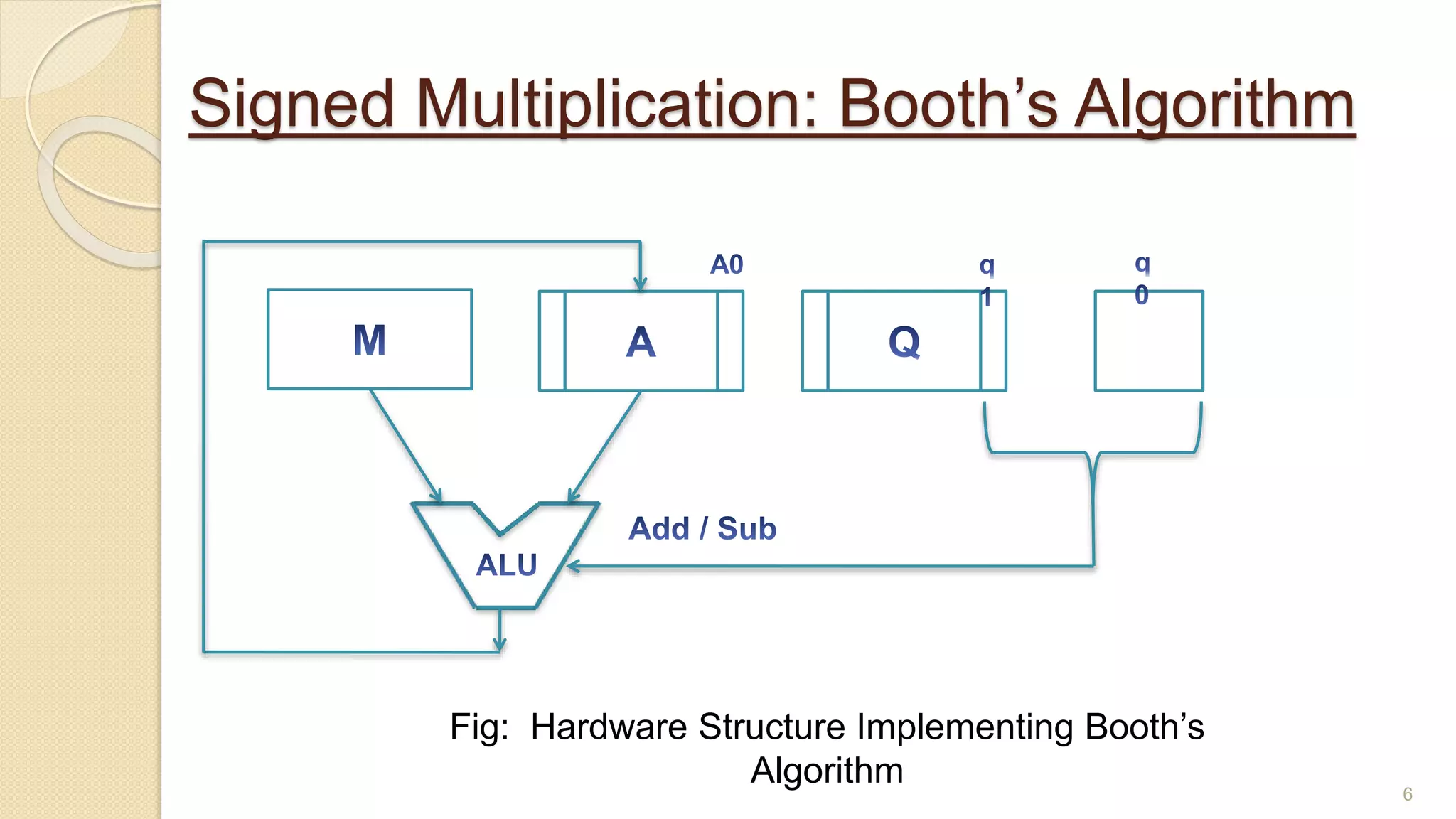
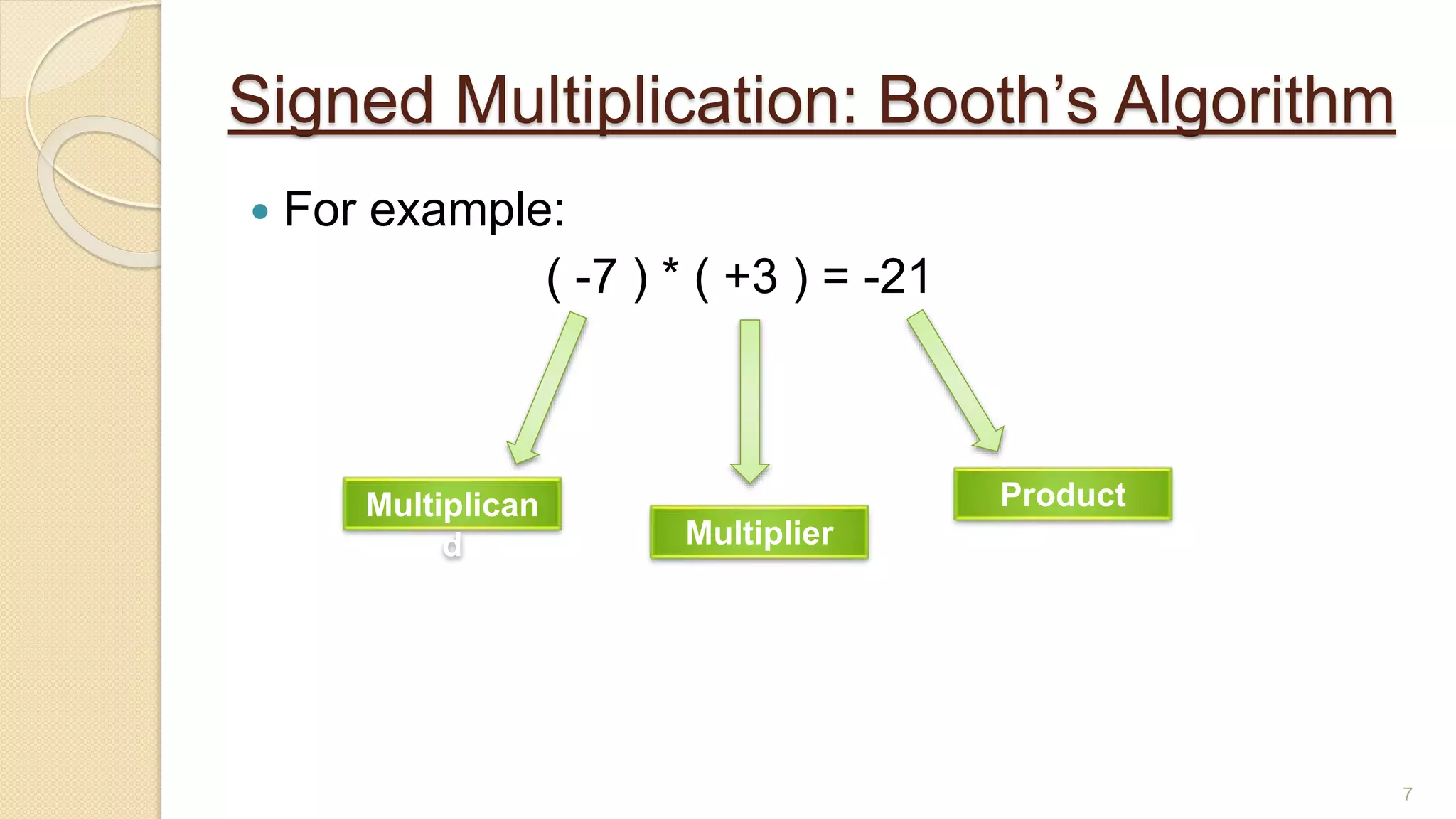
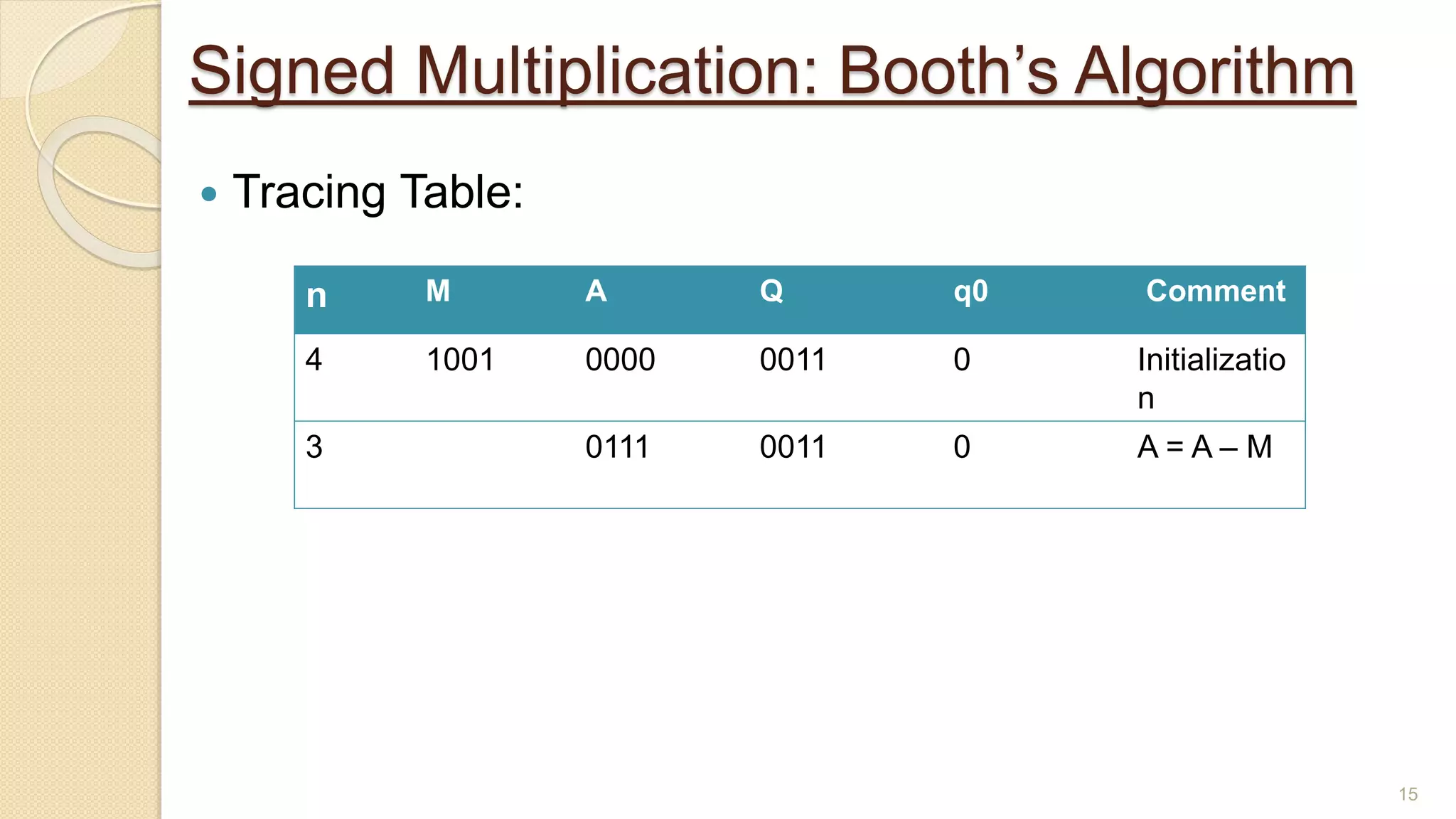
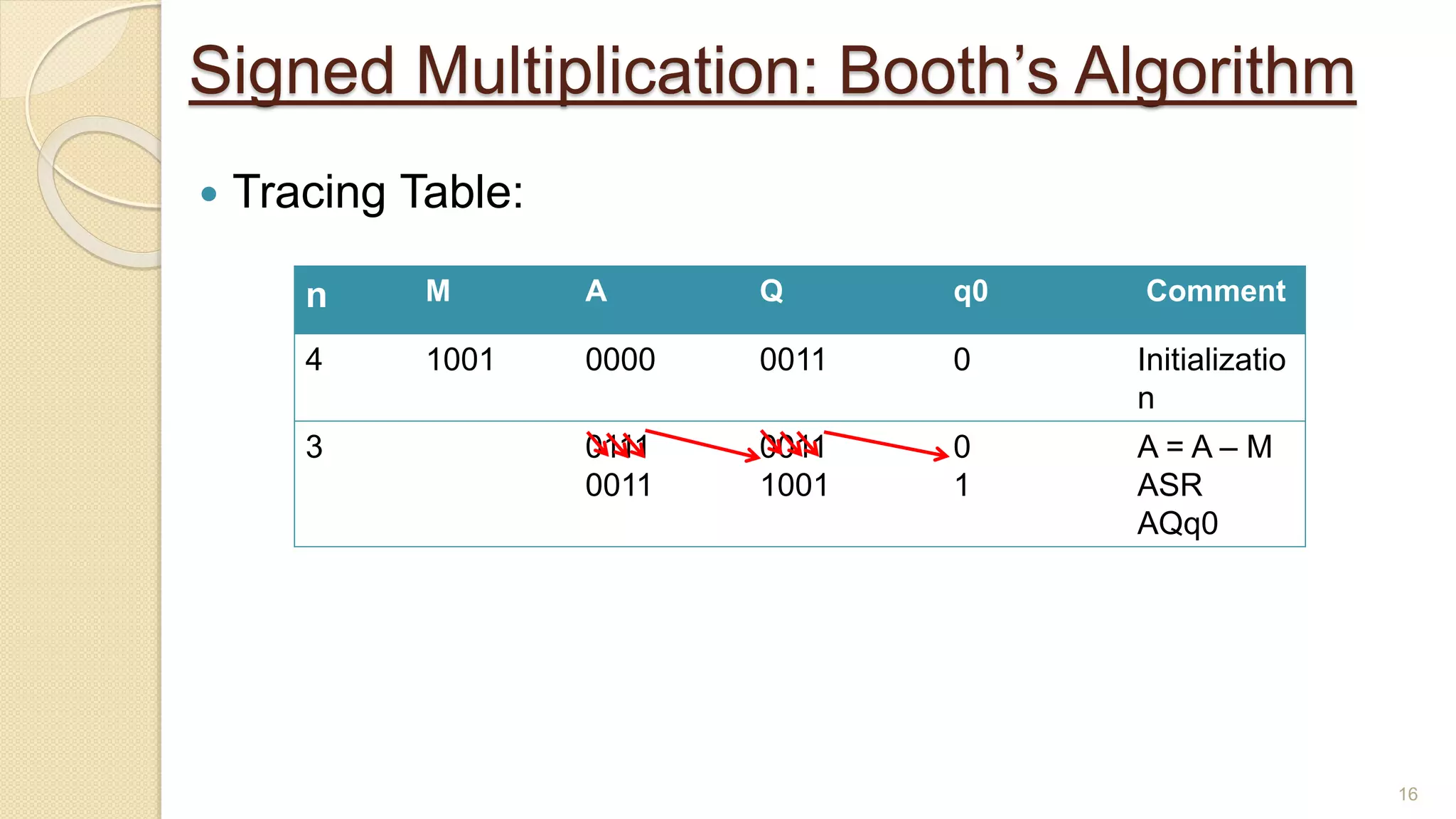
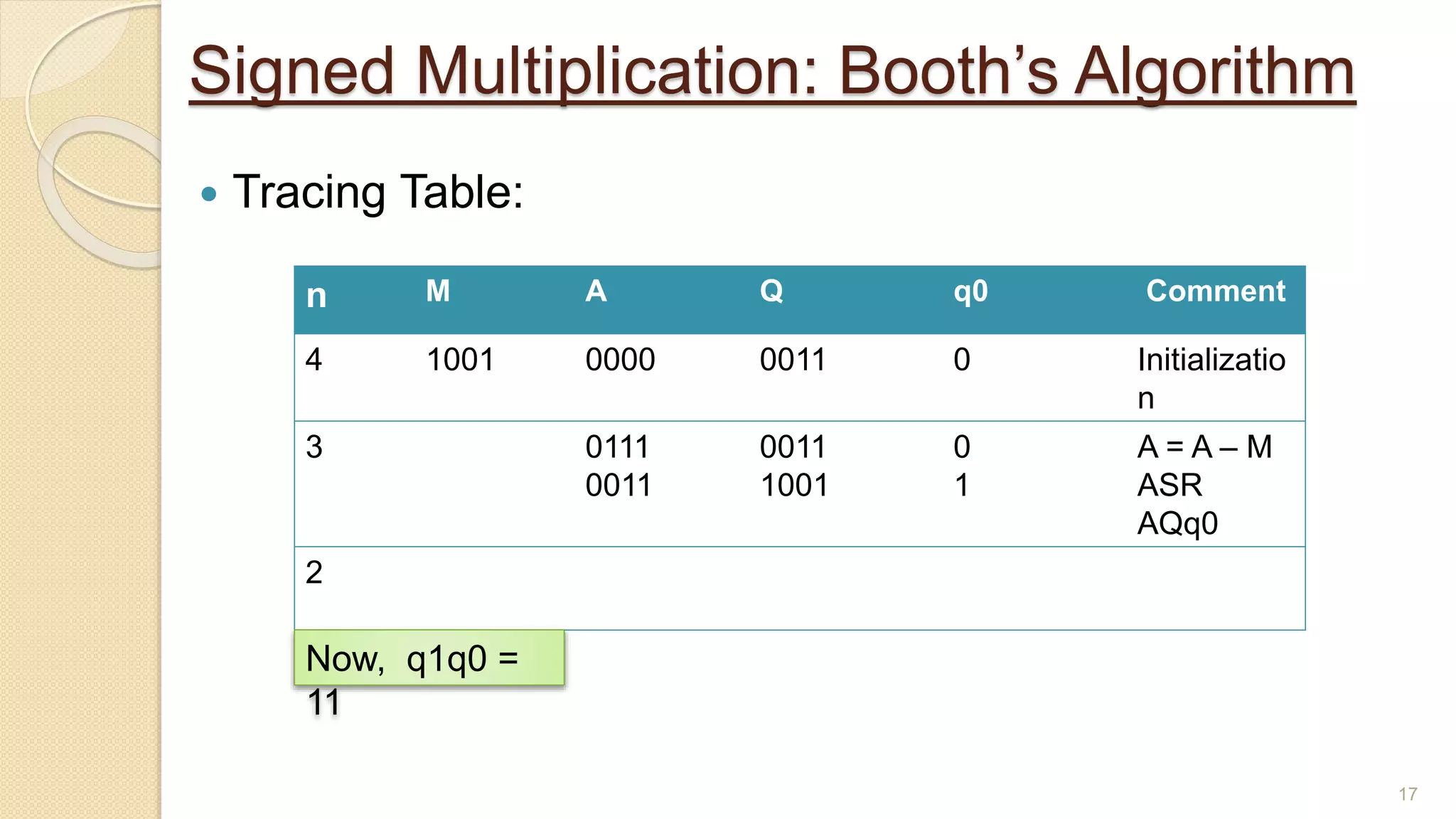
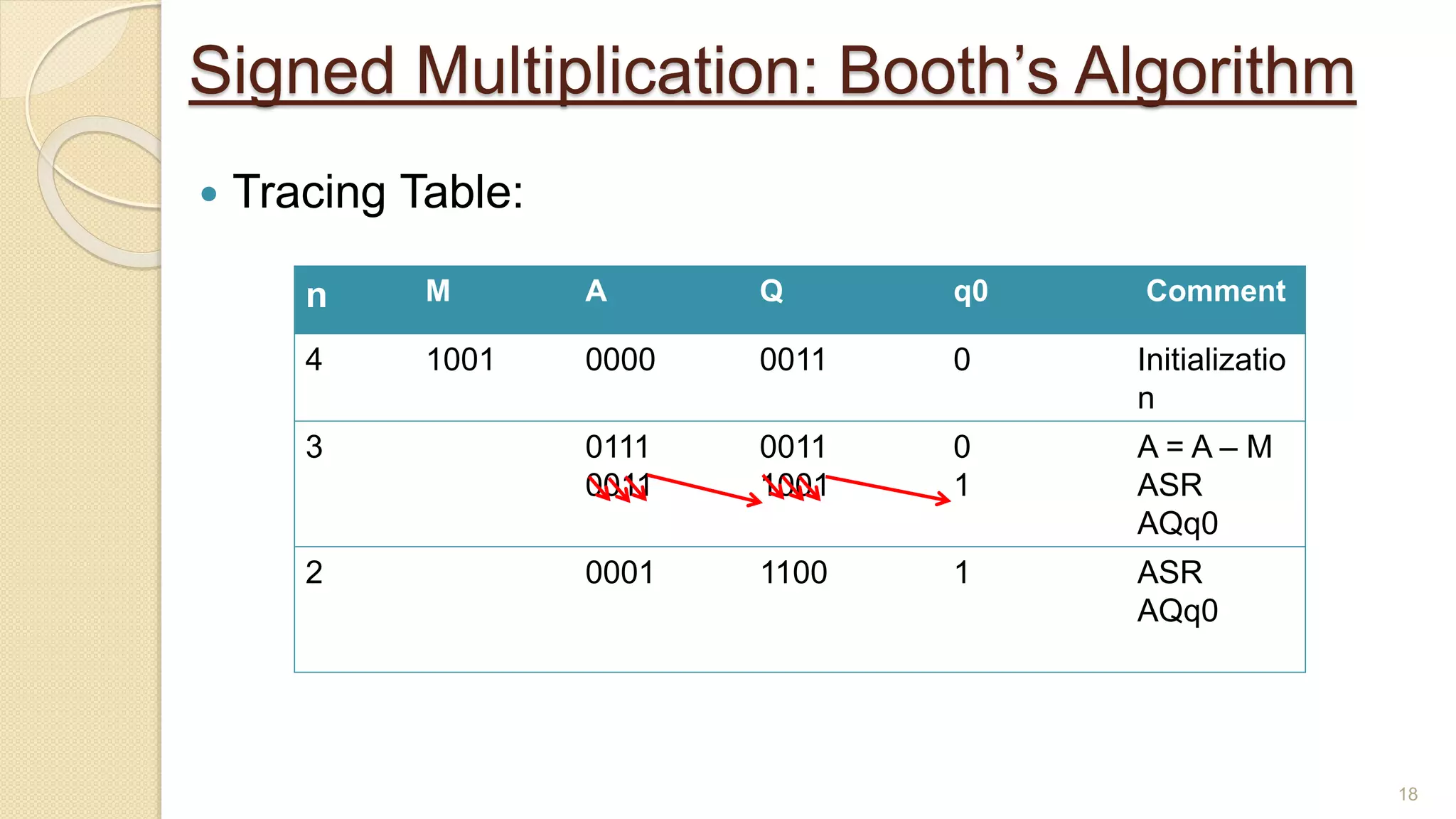
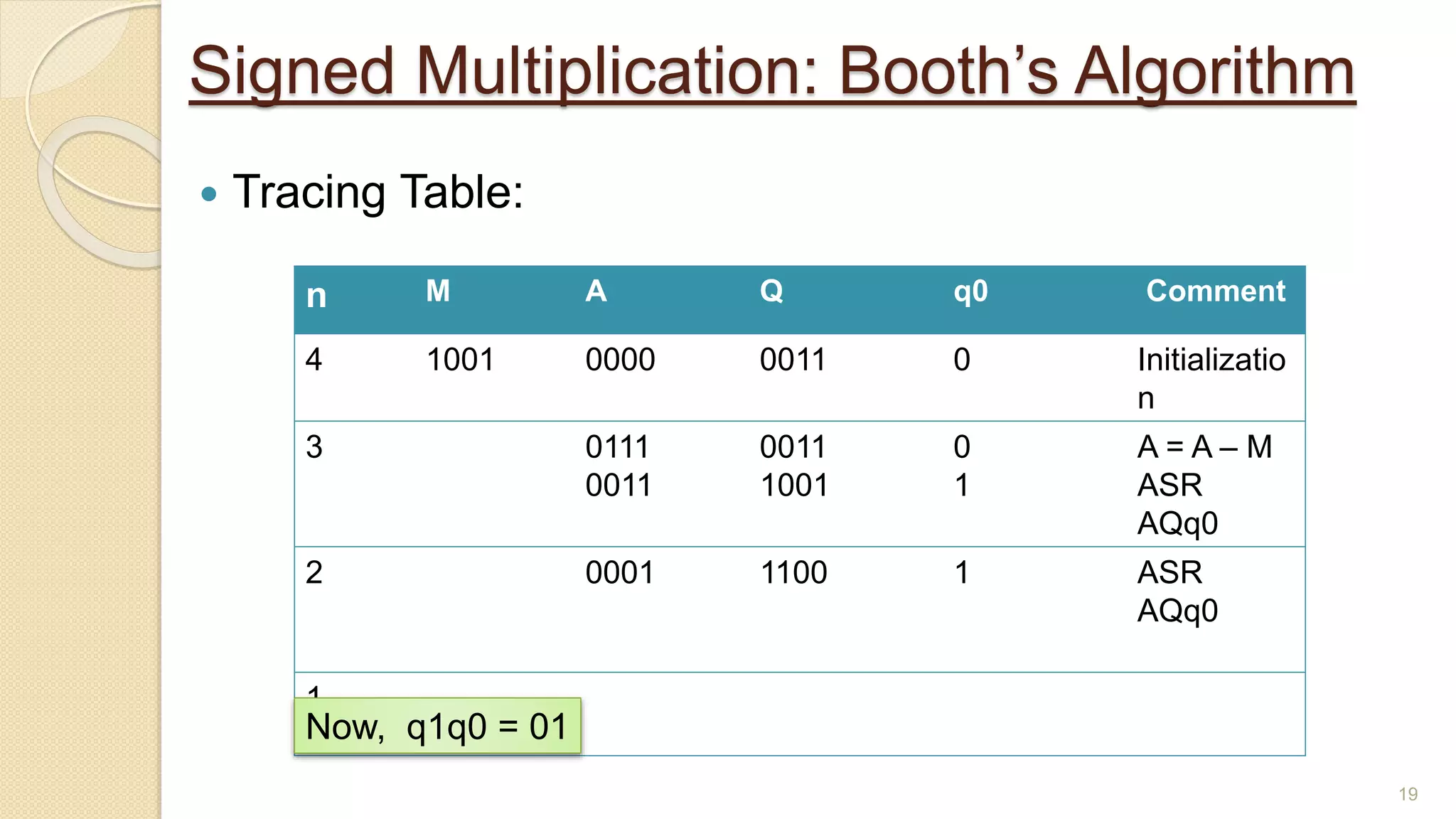
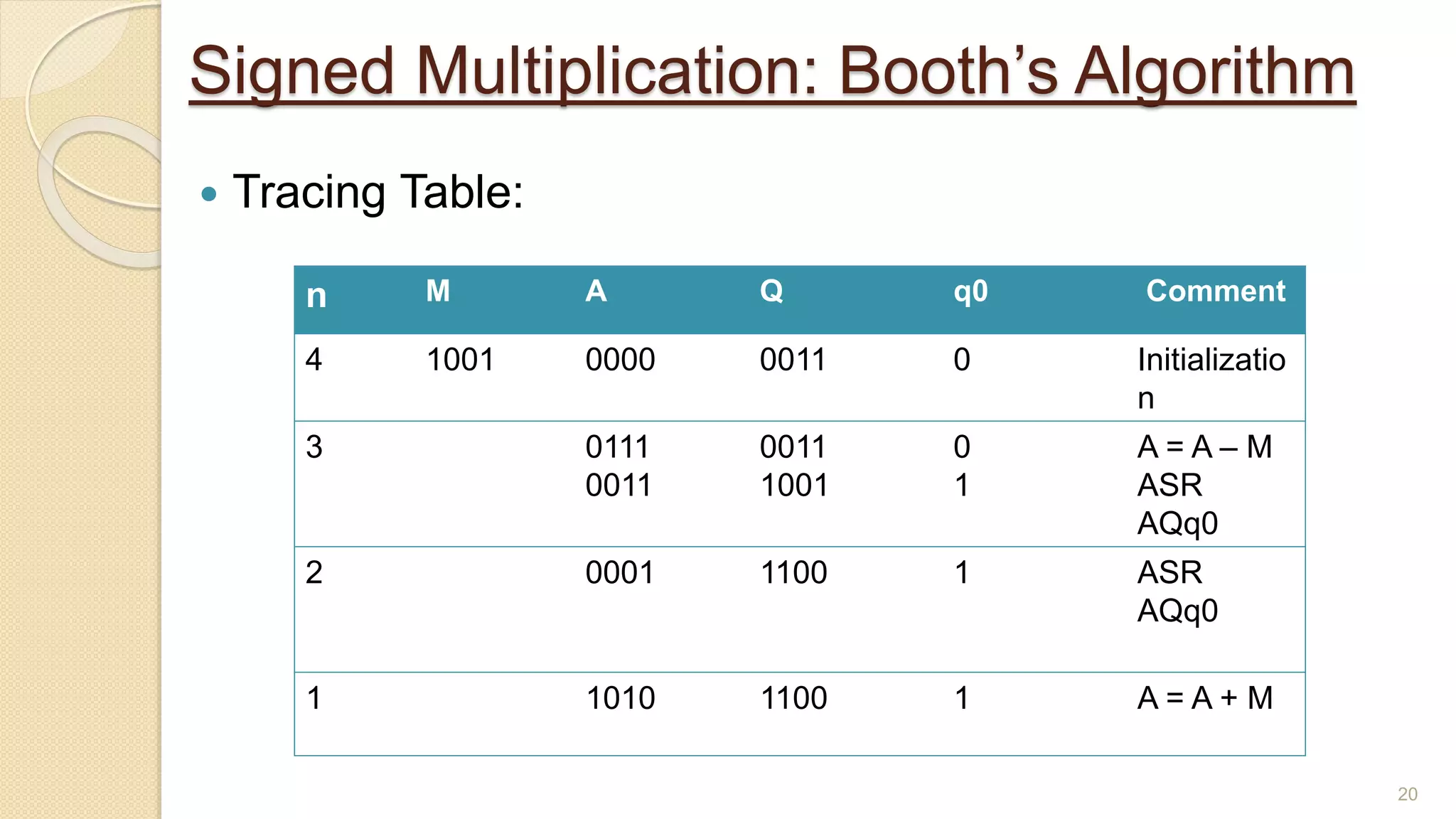
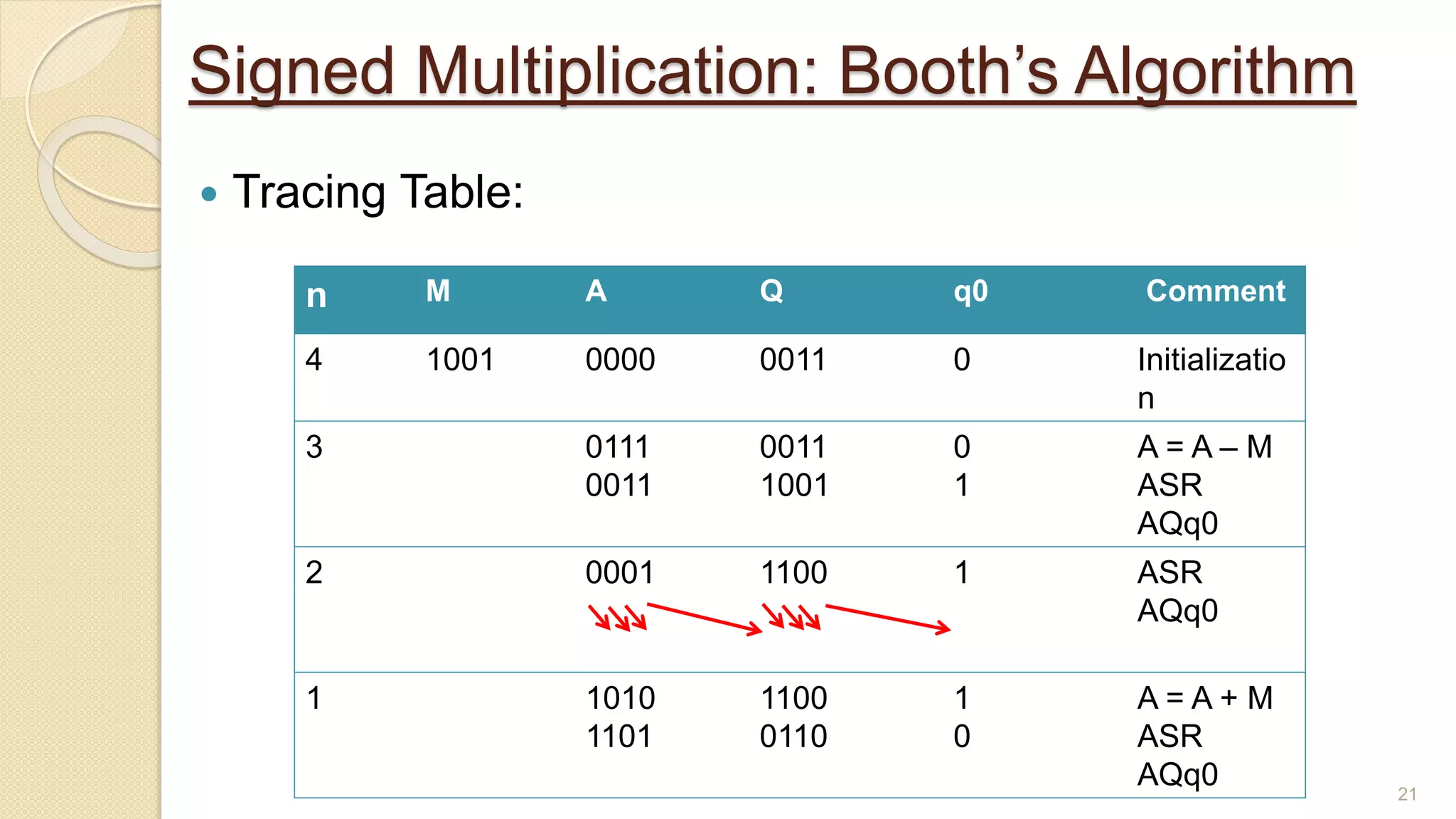
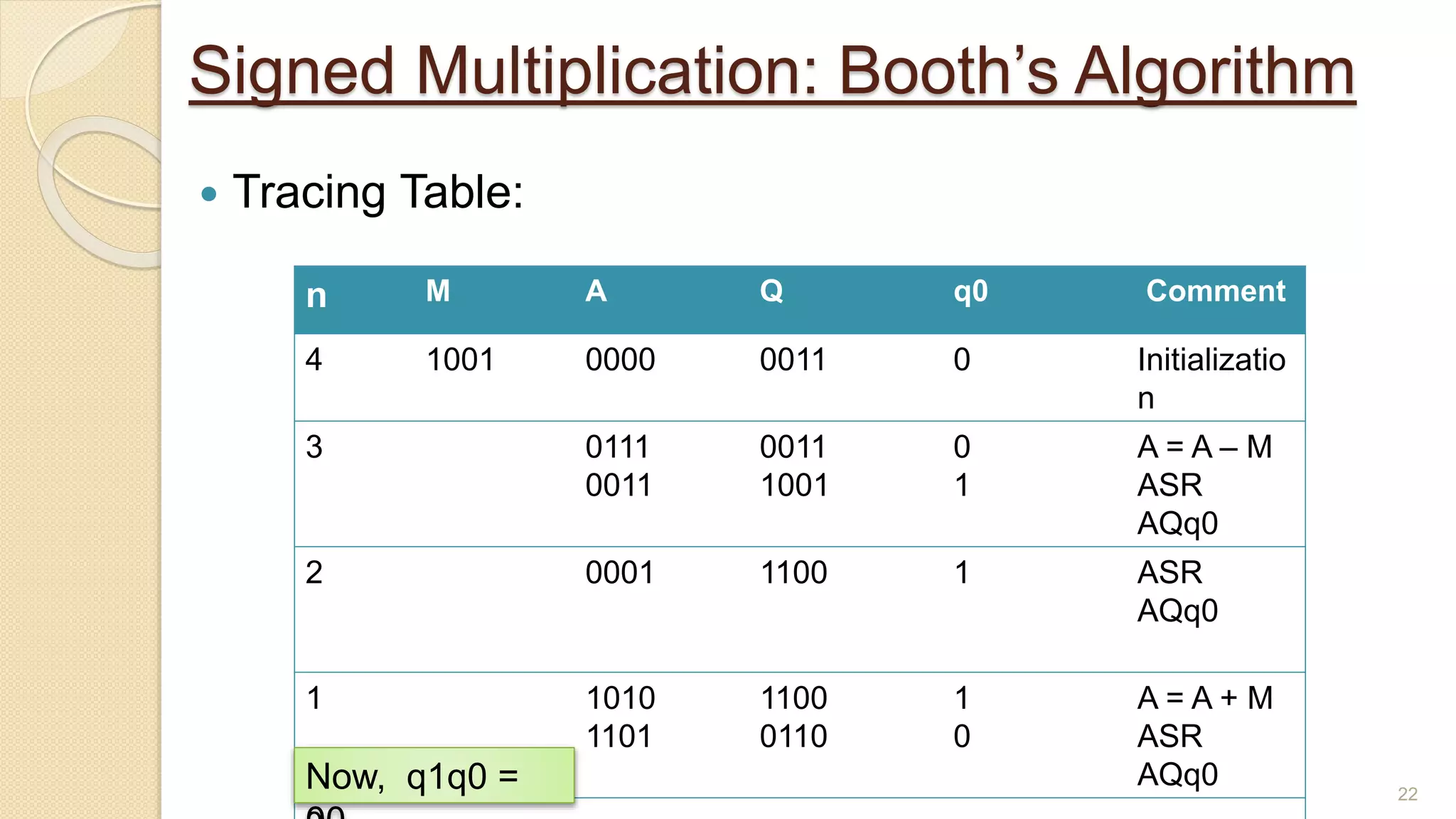
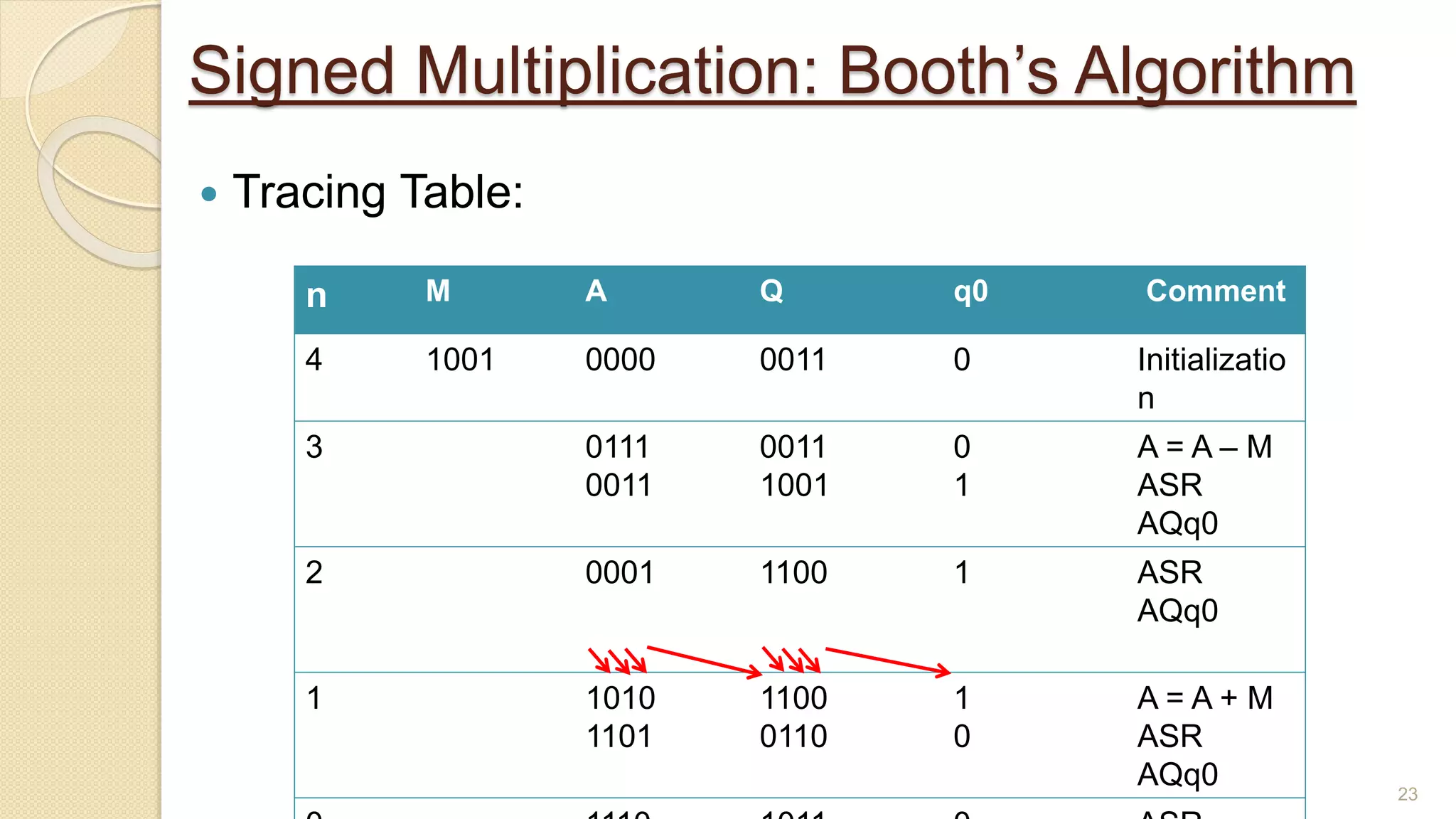
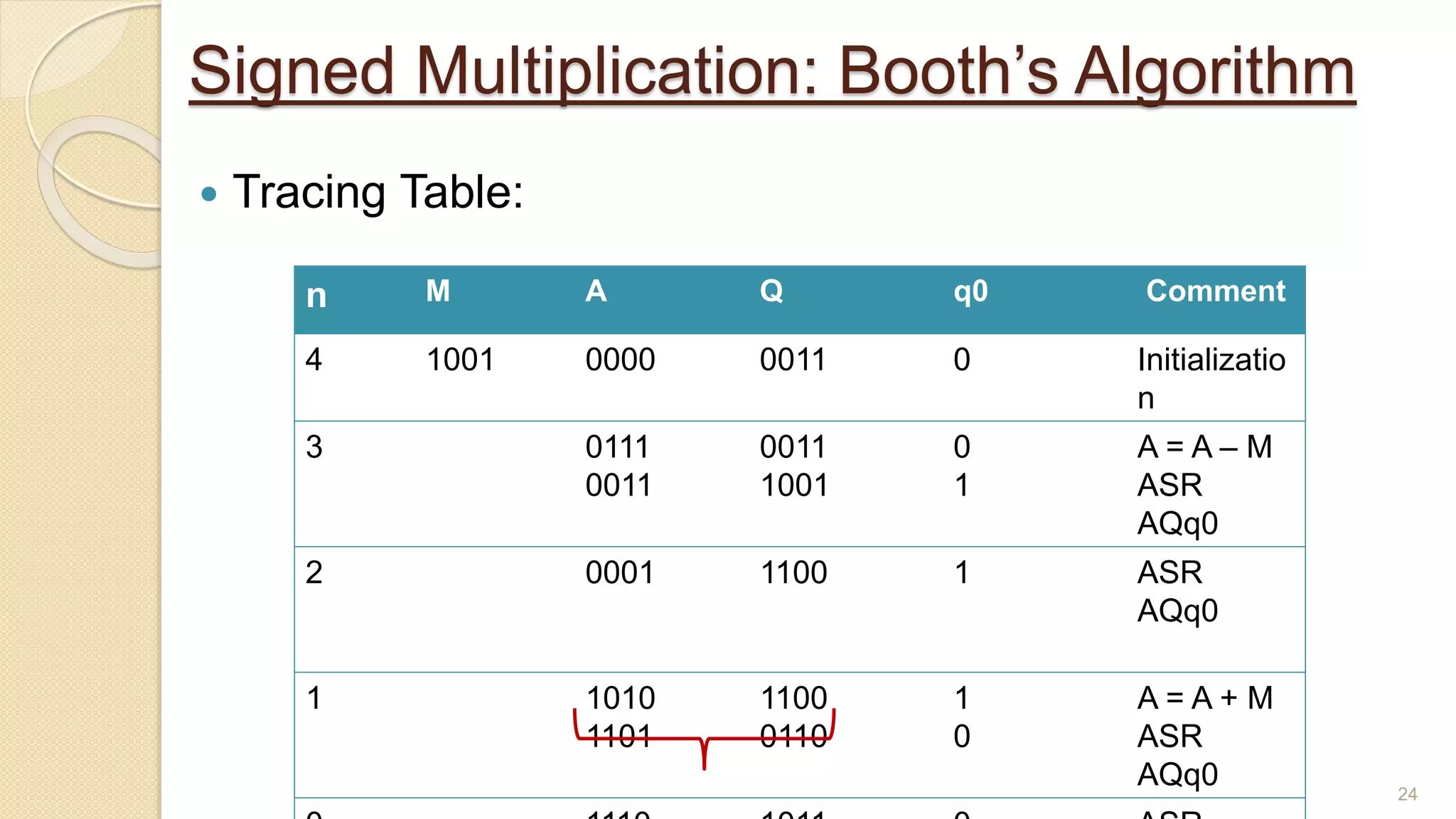
The document presents a lecture on Booth's algorithm for signed multiplication, outlining its history, process, flowchart, and hardware structure. It details how the algorithm multiplies two signed binary numbers using 2's complement notation, including example calculations and tracing tables. The presentation was delivered by Raisa Fabiha to Mostafiz Ahammed at Notre Dame University, Bangladesh on November 30, 2022.

1. Presented for:
Mostafiz
Ahammed
Lecturer,
Department of
CSE,
Notre Dame University,
Bangladesh
Presented by:
Raisa Fabiha
ID - 202120004
Batch – CSE 14
Presentation on Signed Multiplication: Booth’s Algorithm
Fall TRIMESTER – 2022
Department of CSE
Course Code: CSE 3203
Course Title: Computer Architecture
Date of Presentation: 30.11.2022

2. Outline:
2
Topics Page Numbers
Signed Multiplication: Booth’s
Algorithm
03
Flowchart of Booth’s Algorithm 04
Hardware Structure Implementing
Booth’s Algorithm
05
Tracing Table of Booth’s Algorithm 07

3. 3
Signed Multiplication: Booth’s Algorithm
 Booth's multiplication algorithm is a multiplication
algorithm that multiplies two signed binary numbers in 2's
complement notation.
 The algorithm was invented by Andrew Donald Booth in
1950.
 Requires examination of the multiplier bits and shifting of
the partial product.

4. The flowchart for the Signed Multiplication:
Booth’s Algorithm
4

5. 5
Start
M  Multiplicand
Q  Multiplier
q0  0
A  0
n  no. of bits
A = A - M A = A + M
n = n - 1
Arithmetic Shift Right AQq0
Is
n=0?
Result AQ Stop
q1
q0
?
No
Ye
s
10
00
11
01

6. 6
Signed Multiplication: Booth’s Algorithm
Fig: Hardware Structure Implementing Booth’s
Algorithm

7. Signed Multiplication: Booth’s Algorithm
 For example:
( -7 ) * ( +3 ) = -21
7
Multiplican
d Multiplier
Product

8. Signed Multiplication: Booth’s Algorithm
 Tracing Table:
8
n M A Q q0 Comment
4
n = no. of bits

9. Signed Multiplication: Booth’s Algorithm
 Tracing Table:
9
n M A Q q0 Comment
4 1001
Multiplicand, M = -7
= 2’s complement of
0111
= 1001

10. Signed Multiplication: Booth’s Algorithm
 Tracing Table:
10
n M A Q q0 Comment
4 1001 0000
Accumulato
r

11. Signed Multiplication: Booth’s Algorithm
 Tracing Table:
11
n M A Q q0 Comment
4 1001 0000 0011
Multiplier, Q = 3
=
0011

12. Signed Multiplication: Booth’s Algorithm
 Tracing Table:
12
n M A Q q0 Comment
4 1001 0000 0011 0
q0
q1

13. Signed Multiplication: Booth’s Algorithm
 Tracing Table:
13
n M A Q q0 Comment
4 1001 0000 0011 0 Initializatio
n

14. Signed Multiplication: Booth’s Algorithm
 Tracing Table:
14
n M A Q q0 Comment
4 1001 0000 0011 0 Initializatio
n
3
Here, q1q0 =
10

15. Signed Multiplication: Booth’s Algorithm
 Tracing Table:
15
n M A Q q0 Comment
4 1001 0000 0011 0 Initializatio
n
3 0111 0011 0 A = A – M

16. Signed Multiplication: Booth’s Algorithm
 Tracing Table:
16
n M A Q q0 Comment
4 1001 0000 0011 0 Initializatio
n
3 0111
0011
0011
1001
0
1
A = A – M
ASR
AQq0

17. Signed Multiplication: Booth’s Algorithm
 Tracing Table:
17
n M A Q q0 Comment
4 1001 0000 0011 0 Initializatio
n
3 0111
0011
0011
1001
0
1
A = A – M
ASR
AQq0
2
Now, q1q0 =
11

18. Signed Multiplication: Booth’s Algorithm
 Tracing Table:
18
n M A Q q0 Comment
4 1001 0000 0011 0 Initializatio
n
3 0111
0011
0011
1001
0
1
A = A – M
ASR
AQq0
2 0001 1100 1 ASR
AQq0

19. Signed Multiplication: Booth’s Algorithm
 Tracing Table:
19
n M A Q q0 Comment
4 1001 0000 0011 0 Initializatio
n
3 0111
0011
0011
1001
0
1
A = A – M
ASR
AQq0
2 0001 1100 1 ASR
AQq0
1
Now, q1q0 = 01

20. Signed Multiplication: Booth’s Algorithm
 Tracing Table:
20
n M A Q q0 Comment
4 1001 0000 0011 0 Initializatio
n
3 0111
0011
0011
1001
0
1
A = A – M
ASR
AQq0
2 0001 1100 1 ASR
AQq0
1 1010 1100 1 A = A + M

21. Signed Multiplication: Booth’s Algorithm
 Tracing Table:
21
n M A Q q0 Comment
4 1001 0000 0011 0 Initializatio
n
3 0111
0011
0011
1001
0
1
A = A – M
ASR
AQq0
2 0001 1100 1 ASR
AQq0
1 1010
1101
1100
0110
1
0
A = A + M
ASR
AQq0

22. Signed Multiplication: Booth’s Algorithm
 Tracing Table:
22
n M A Q q0 Comment
4 1001 0000 0011 0 Initializatio
n
3 0111
0011
0011
1001
0
1
A = A – M
ASR
AQq0
2 0001 1100 1 ASR
AQq0
1 1010
1101
1100
0110
1
0
A = A + M
ASR
AQq0
Now, q1q0 =

23. Signed Multiplication: Booth’s Algorithm
 Tracing Table:
23
n M A Q q0 Comment
4 1001 0000 0011 0 Initializatio
n
3 0111
0011
0011
1001
0
1
A = A – M
ASR
AQq0
2 0001 1100 1 ASR
AQq0
1 1010
1101
1100
0110
1
0
A = A + M
ASR
AQq0

24. Signed Multiplication: Booth’s Algorithm
 Tracing Table:
24
n M A Q q0 Comment
4 1001 0000 0011 0 Initializatio
n
3 0111
0011
0011
1001
0
1
A = A – M
ASR
AQq0
2 0001 1100 1 ASR
AQq0
1 1010
1101
1100
0110
1
0
A = A + M
ASR
AQq0

25. Signed Multiplication: Booth’s Algorithm
 Result: 1110 1011
25
0001 0100
+1
0001 0101 = - 21

26. Signed Multiplication: Booth’s Algorithm
 Result: 1110 1011
26
2’s complement
representation:
-128 + 64 + 32 + 8 + 2 + 1 = -
21

27. References:
27
1. https://en.wikipedia.org/wiki/Booth%27s_multiplicat
ion_algorithm

28. Thank You
28

29. 29
?